Đề thi học kì 2 Toán 6 - Đề số 2 - Chân trời sáng tạoTải vềPhần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Cho dãy chữ cái: H, A, N, O, I. Trong dãy trên có bao nhiêu chữ cái có tâm đối xứng? A. \(2\) B. \(3\) C. \(4\) D. \(5\) Câu 2: Viết tên góc ở hình vẽ bên bằng kí hiệu. A. \(\angle Axy\) B. \(\angle xyA\) C. \(\angle xAy\) D. \(\angle xy\) Câu 3: Bạn Hòa đi siêu thị mua thực phẩm tổng hết 500 nghìn đồng. Ngày hôm đó siêu thị giảm giá 20%. Số tiền Hòa phải trả nếu không được giảm là: A. 600 nghìn đồng B. 625 nghìn đồng C. 450 nghìn đồng D. 400 nghìn đồng Câu 4: Gieo một con xúc xắc sáu mặt 13 lần liên tiếp, có 7 lần xuất hiện mặt hai chấm thì xác suất thực nghiệm xuất hiện mặt hai chấm là: A. \(\dfrac{7}{{13}}\) B. \(\dfrac{2}{7}\) C. \(\dfrac{2}{{13}}\) D. \(\dfrac{9}{{13}}\) Phần II. Tự luận (8 điểm): Bài 1: (1 điểm) Thực hiện các phép tính: \(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}}\) \(b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right)\) Bài 2: (2 điểm) Tìm x biết: a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\) b) \(3 \cdot {\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\) c) \(12,3:x - 4,5:x = 15\) d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\) Bài 3 (2 điểm) Một lớp học có 50 học sinh gồm: giỏi, khá, trung bình. Số học sinh trung bình chiếm \(\dfrac{3}{{10}}\) số học sinh cả lớp. Số học sinh khá bằng \(40\% \) số học sinh còn lại. a) Tính số học sinh mỗi loại của lớp đó. b) Tính tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp. Bài 4: (2,5 điểm) Cho hai điểm \(M,N\) thuộc tia \(Ox\) sao cho \(OM = 2cm;ON = 5cm\). Điểm \(P\) thuộc tia đối của tia \(Ox\) sao cho \(OP = 3cm\). a) Điểm \(M\) có nằm giữa hai điểm \(O\) và \(N\) không? Tại sao? Tính \(MN.\) b) So sánh\(MN\) và \(OP.\) c) Gọi \(I\) là trung điềm của \(OM\). Tính \(IO\) và \(IP.\) d) Điểm \(I\) có là trung điềm của \(NP\) không? Tại sao? Bài 5: (0,5 điểm) Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{3n - 4}}{{2 - n}}\). Lời giải Phần I: Trắc nghiệm
Câu 1 Phương pháp: Sử dụng lý thuyết tâm đối xứng của một hình. Cách giải: Các chữ cái có tâm đối xứng là: H, N, O, I Chữ A không có tâm đối xứng. Chọn C. Câu 2 Phương pháp: Hai tia Ox, Oy phân biệt tạo thành góc \(\angle xOy\). Cách giải: Góc đã cho được kí hiệu là \(\angle xAy\). Chọn C. Câu 3 Phương pháp: Sau khi được giảm 20%, số tiền phải trả bằng 80% số tiền ban đầu. Ta lấy số hết Hòa đã trả chia 80%. Cách giải: Số tiền Hòa phải trả là: \(500:\dfrac{{100 - 20}}{{100}} = 625\)(nghìn đồng) Chọn B. Câu 4 Phương pháp Xác suất thực nghiệm xuất hiện mặt i chấm khi tung xúc xắc nhiều lần là: Số lần xuất hiện mặt i chấm : Tổng số lần tung xúc xắc. Cách giải: Xác suất thực nghiệm xuất hiện mặt hai chấm khi tung xúc xắc nhiều lần là: \(\dfrac{7}{{13}}\). Chọn A. Phần II: Tự luận Bài 1 Phương pháp a) Nhóm các số hạng có cùng mẫu số, rồi thực hiện cộng trừ các phân số có cùng mẫu số. b) Tách hỗn số thành hai phần: phần nguyên và phần phân số, rồi cộng phần nguyên với nhau, cộng phần phân số với nhau. Chú ý: Muốn cộng (trừ) hai phân số có cùng mẫu số, ta cộng (trừ) tử số với nhau và giữ nguyên mẫu số. Cách giải: \(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}} = \left( {\dfrac{{31}}{{17}} - \dfrac{{14}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}}} \right) = \dfrac{{17}}{{17}} + \dfrac{{ - 13}}{{13}} = 1 + \left( { - 1} \right)\, = 0\) \(\begin{array}{l}b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - \left( {2 + \dfrac{3}{7} + 3 + \dfrac{5}{{11}}} \right) = 7 + \dfrac{5}{{11}} - 2 - 3 - \dfrac{3}{7} - \dfrac{5}{{11}}\\\, = \left( {7 - 2 - 3} \right) + \left( {\dfrac{5}{{11}} - \dfrac{5}{{11}}} \right) - \dfrac{3}{7} = 2 + 0 - \dfrac{3}{7}\, = \dfrac{{11}}{7}\end{array}\)
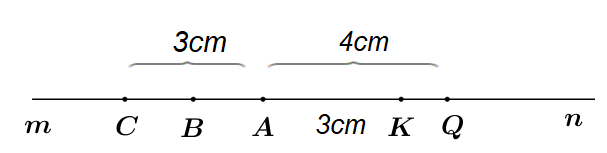
Bài 2 Phương pháp Áp dụng các kiến thức: - Sử dụng các công thức lũy thừa và quy tắc bỏ ngoặc để tìm x - Áp dụng quy tắc chuyển vế đổi dấu x. - Đặt điều kiện để các phân số có nghĩa, tìm x. Chú ý sau khi tìm được \(x\) cần đối chiếu với điều kiện rồi kết luận \(x\) Cách giải: a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\) \(\begin{array}{l}\dfrac{1}{3}x + \dfrac{2}{5}x - \dfrac{2}{5} = 0\\\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right)x = \dfrac{2}{5}\\\dfrac{{11}}{{15}}x = \dfrac{2}{5}\end{array}\) \(x = \dfrac{2}{5}:\dfrac{{11}}{{15}}\) \(\begin{array}{l}x = \dfrac{2}{5} \cdot \dfrac{{15}}{{11}}\\x = \dfrac{6}{{11}}\end{array}\) Vậy \(x = \dfrac{6}{{11}} \cdot \) b) \(3.{\left( {3x - \dfrac{1}{2}} \right)^3} + \dfrac{1}{9} = 0\) \(\begin{array}{l}3.{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{9}:3\\{\left( {3x - \dfrac{1}{2}} \right)^3} = - \dfrac{1}{{27}} = \left( {\dfrac{{ - 1}}{3}} \right)\end{array}\) \( \Rightarrow 3x - \dfrac{1}{2} = {\dfrac{{ - 1}}{3}^3}\) \(\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3x = \dfrac{{ - 1}}{3} + \dfrac{1}{2}{\kern 1pt} {\kern 1pt} \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3x = \dfrac{{ - 2}}{6} + \dfrac{3}{6}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3x = \dfrac{1}{6}{\kern 1pt} {\kern 1pt} \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x = \dfrac{1}{{18}}\end{array}\) Vậy \(x = \dfrac{1}{{18}} \cdot \) c) \(12,3:x - 4,5:x = 15\) \(\begin{array}{l}\left( {12,3 - 4,5} \right):x = 15\\7,8:x = 15\\x = 7,8:15\\x = 0,52\end{array}\) Vậy \(x = 0,52\) d) \(\dfrac{{3 - x}}{{5 - x}} = {\left( {\dfrac{{ - 3}}{5}} \right)^2}\) Điều kiện: \(5 - x \ne 0 \Leftrightarrow x \ne 5.\) \(\begin{array}{*{20}{l}}{ \Rightarrow \dfrac{{3 - x}}{{5 - x}} = \dfrac{9}{{25}}}\\{ \Rightarrow \left( {3 - x} \right).25 = 9.\left( {5 - x} \right)}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 75 - 25x = 45 - 9x{\kern 1pt} }\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 25x + 9x = 45 - 75}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 16x = {\rm{ \;}} - 30}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x = \dfrac{{ - 30}}{{ - 16}} = \dfrac{{15}}{8}}\end{array}\) Vậy \(x = \dfrac{{15}}{8} \cdot \) Bài 3 Phương pháp: a) Áp dụng quy tắc: Muốn tìm \(\dfrac{m}{n}{\kern 1pt} \) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\) b) Áp dụng quy tắc tìm tỉ số phần trăm của hai số : Muốn tìm tỉ số phần trăm của hai số \(a\) và \(b\), ta nhân \(a\) với 100 rồi chia cho \(b\) và viết kí hiệu \(\% \) vào kết quả : \(\dfrac{{a.100}}{b}\% \). Cách giải: a) Lớp học đó có số học sinh trung bình là : \(50.\dfrac{3}{{10}} = 15\) (học sinh) Lớp đó có số học sinh giỏi và khá là : \(50 - 15 = 35\) (học sinh) Lớp đó có số học sinh khá là : \(35.40\% {\rm{\;}} = 14\) (học sinh) Lớp đó có số học sinh giỏi là : \(35 - 14 = 21\) (học sinh) b) Tỉ số phần trăm của học sinh giỏi so với số học sinh cả lớp là: \(21:50.100\% {\rm{\;}} = 42\% \) Bài 4 Phương pháp a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ. b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK. Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK. c) Tính BA. Chứng minh A nằm giữa B và K. Tính BK = BA + AK. So sánh BK và AQ. Cách giải:
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q. => AK + KQ = AQ => 3 + KQ = 4 => KQ = 4 – 3 => KQ = 1 (cm) b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K. => CK = AC + AK => CK = 3 + 3 => CK = 6 (cm) Ta có: A nằm giữa C và K. AC = AK = 3cm. => A là trung điểm của CK. c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm). Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K. => BK = BA + AK => BK = 1,5 + 3 => BK = 4,5 (cm) Mà AQ = 4 (cm) => BK > AQ. Bài 5 Phương pháp Phân tích \(A = a + \dfrac{b}{{2 - n}}\), với \(a,\,\,b \in \mathbb{Z}\). Để \(A \in \mathbb{Z}\) thì \(2 - n \in U\left( b \right)\). Cách giải: \(\begin{array}{l}A = \dfrac{{3n - 4}}{{2 - n}} = \dfrac{{3n - 6 + 2}}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{3n - 6}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = \dfrac{{ - 3\left( { - n + 2} \right)}}{{ - n + 2}} + \dfrac{2}{{ - n + 2}}\\\,\,\,\,\, = - 3 + \dfrac{2}{{ - n + 2}}\end{array}\) Để A nhận giá trị nguyên thì \( - 3 + \dfrac{2}{{ - n + 2}} \in \mathbb{Z} \Rightarrow \dfrac{2}{{ - n + 2}} \in \mathbb{Z}\)\( \Rightarrow - n + 2 \in \left\{ { \pm 1; \pm 2} \right\}\) Ta có bảng giá trị sau:
Vậy \(n \in \left\{ {1;3;0;4} \right\}\).
|














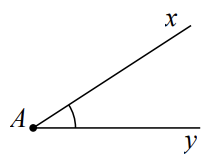






Danh sách bình luận