Dạng 4. Xác suất thực nghiệm Chủ đề 11 Ôn hè Toán 6

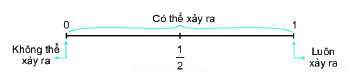
Lý thuyết

I. Khả năng xảy ra của một sự kiện

Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.

Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.

Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.

II. Xác suất thực nghiệm

Thực hiện lặp đi lặp lại một hoạt động nào đó n lần.

Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số

\(\dfrac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động

Được gọi là xác suất thực nghiệm của sự kiện A.

Nhận xét: Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm, trò chơi. 

Bài tập

Bài 1:

Bài toán “Ước lượng số cá trong hồ”

- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.

- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.

a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”

b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.

Bài 2:

Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày

b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.

Câu 3:

Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Sơn phải chờ xe dưới \(1\) phút

b) Sơn phải chờ xe từ \(5\) phút trở lên 

Lời giải chi tiết:

Bài 1:

Bài toán “Ước lượng số cá trong hồ”

- Sau khoảng thời gian nuôi cá, những người cư dân muốn biết xem số cá hiện có trong hồ là bao nhiêu để có những kế hoạch nuôi đúng cách. Vấn đề đặt ra là không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được, sẽ ảnh hưởng không tốt đến cá. Hãy xét một giải pháp sau đây.

- Đầu tiên, bác Thắng, một ngư dân có kinh nghiệm, bắt 60 con cá lên và đánh dấu, sau đó thả lại vào hồ. Ngày hôm sau, bác Thắng bắt lên 24 con cá và đếm được 3 con cá đã được đánh dấu.

a) Tính xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu”

b) Giải thích vì sao từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ? Hãy ước tính số cá trong hồ.

Phương pháp

Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm.

Lời giải

a) Xác suất thực nghiệm của sự kiện “Cá bắt lên được đã đánh dấu” là: \(\dfrac{3}{{24}} = 12,5\% \)

b) Từ xác suất thực nghiệm trên có thể ước tính được số cá trong hồ như sau:

Trong số cá bắt lên, số cá được đánh dấu chiếm 12,5%

Toàn bộ số cá được đánh dấu trong hồ là 60 con

Có thể ước lượng 60 con được đánh dấu này tương ứng với 12,5% số cá trong hồ

Vậy, ước lượng được số cá trong hồ là: \(60:12,5\%  = 480\)\(\left( {{\rm{con}}} \right)\)

Bài 2:

Tổng hợp kết quả xét nghiệm Covid ở một bệnh viện trong \(4\) ngày ta thu được bảng sau:

a) Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính theo từng ngày

b) Hãy tính tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày.

Phương pháp

Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm

Lời giải

a) Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ nhất” là:

\(\dfrac{{15}}{{150}} = \dfrac{1}{{10}}\)

Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ hai” là: \(\dfrac{{21}}{{200}}\)

Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là: \(\dfrac{{17}}{{180}}\)

Xác suất thực nghiệm của sự kiện: “một ca xét nghiệm có kết quả dương tính trong ngày thứ ba” là:

\(\dfrac{{24}}{{220}} = \dfrac{6}{{55}}\)

b) Tổng số ca dương tính trong \(4\) ngày là: \(15 + 21 + 17 + 24 = 77\)

Tổng số ca xét nghiệm trong \(4\) ngày là: \(150 + 200 + 180 + 220 = 750\)

Tỉ lệ số ca dương tính và số ca xét nghiệm trong \(4\) ngày là: \(\dfrac{{77}}{{750}}\)

Câu 3:

Hàng ngày Sơn đều đi xe buýt tới trường. Sơn ghi lại thời gian chờ xe của mình trong \(20\) lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Sơn phải chờ xe dưới \(1\) phút

b) Sơn phải chờ xe từ \(5\) phút trở lên

Phương pháp

Xác suất thực nghiệm của một sự kiện bằng số lần xảy ra sự kiện : tổng số lần làm thực nghiệm

Lời giải

a) Xác suất thực nghiệm của sự kiện: “Sơn phải chờ xe dưới \(1\) phút” là \(\dfrac{4}{{20}} = \dfrac{1}{5}\)

b) Số lần Sơn phải chờ xe từ \(5\) phút trở lên là: \(4 + 2 = 6\)

Xác suất thực nghiệm của sự kiện:” Sơn phải chờ xe từ \(5\) phút trở lên” là \(\dfrac{6}{{20}} = \dfrac{3}{{10}}\)