Dạng 3. Tìm x Chủ đề 5 Ôn hè Toán 6Tải về* Thứ tự thực hiện phép tính: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
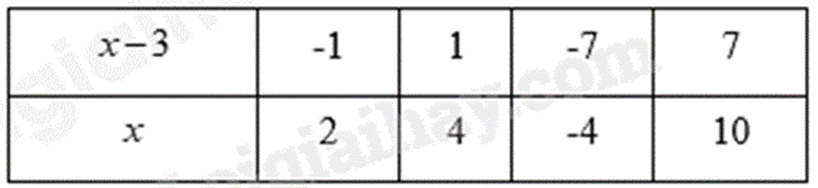
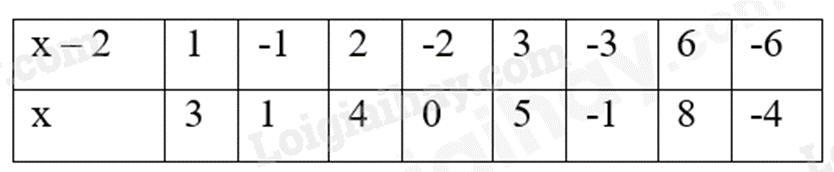
Lý thuyết * Thứ tự thực hiện phép tính: - Với biểu thức không có dấu ngoặc: + Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải. + Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ. - Với biểu thức có dấu ngoặc: Ta thực hiện theo thứ tự: ( ) trước, rồi đến [ ], sau đó mới đến ngoặc { } * Quy tắc dấu ngoặc: Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc: - Có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc: a + (b+ c – d) = a + b + c – d - Có dấu “-”, thì phải đổi dấu tất cả các số hạng trong ngoặc: a – (b + c – d) = a – b – c + d * Cách tìm x: - Tìm số hạng chưa biết trong một tổng: a + x = b (hoặc x + a = b) thì x = b - a - Tìm số bị trừ trong một hiệu: x – a = b thì x = b + a - Tìm số trừ trong một hiệu: a – x = b thì x = a - b - Tìm thừa số chưa biết trong một tích: a.x = b (hoặc x.a = b) thì x = b : a - Tìm số bị chia trong một thương: x : a = b thì x = b . a - Tìm số chia trong một thương: a : x = b thì x = a : b - Nếu a . b = 0 thì a = 0 hoặc b = 0. Bài tập Bài 1: Tìm \(x\) biết \(x - \left( { - 43} \right) = \left( { - 3} \right)\). A. \(x = 43\). B. \(x = {\rm{\;}} - 40\). C. \(x = {\rm{\;}} - 46\). D. \(x = 46\). Bài 2: Giá trị của \(x\) biết \( - 20 - x = 96\) là: A. 116. B. -76. C. -116. D. 76. Bài 3: Cho \(25 - \left( {x + 15} \right) = {\rm{\;}} - 415 - \left( { - 215 - 415} \right)\) thì \(x\) bằng A. -205. B. 175. C. -175. D. 205. Bài 4: Tìm \(x\) biết \(2\left( {x - 5} \right) - 3\left( {x - 7} \right) = {\rm{\;}} - 2.\) A. \(x = 13\). B. \(x = 5\). C. \(x = 7\). D. \(x = 6\). Bài 5: Cho \(\left( { - 4} \right).\left( {x - 3} \right) = 20.\) Tìm \(x\). A. 8. B. -5. C. -2. D. 2. Bài 6: Tìm x, biết: a) \((x - 125).21 = 0\) b) \((2x - 16):12 = - 8\) c) \((3x - 24).( - 39) = 117\) d) \(123 - (2x - 3) = ( - 118)\) e) \((27 - x).(3x + 9).(42 - 6x) = 0\) Bài 7: Tìm \(x\), biết: a) \({(x + 7)^2} = 36\) b) \(2.{(x + 3)^2} - 24 = - 6\) Bài 8: Tìm số nguyên \(x\), biết: a) \(x - 10 = {\rm{\;}} - 65\) b) \(32:\left( {x + 125} \right) = - {4^2}\) c) \(20 - 5\left( {2 - x} \right) = 45\) d) \(29 \vdots x\) Bài 9: Tìm số nguyên x, biết: a) \(x - 42 = \left( { - 18} \right) + \left( { - 16} \right)\) b) \(\left( {5x - 3} \right) + 85 = 32\) c) \(2{\left( {x + 1} \right)^2} + 4 = {2^2}{.3^2}\) d) \(7 \vdots \left( {x - 3} \right)\) Bài 10: Tìm số nguyên x, sao cho: a) \(\frac{6}{{x - 2}}\) là số nguyên b) \(\frac{{4x - 3}}{{x + 2}}\) là số nguyên ----HẾT---- Lời giải chi tiết: Bài 1: Tìm \(x\) biết \(x - \left( { - 43} \right) = \left( { - 3} \right)\). A. \(x = 43\). B. \(x = {\rm{\;}} - 40\). C. \(x = {\rm{\;}} - 46\). D. \(x = 46\). Phương pháp - Xác định: +) \(x\) ở vị trí là số bị trừ +) \(\left( { - 43} \right)\) ở vị trí là số trừ +) \(\left( { - 3} \right)\) ở vị trí là hiệu +) Số bị trừ = Hiệu + Số trừ - Đưa về cộng hai số nguyên âm để tìm $x.$ Lời giải Ta có \(x - \left( { - 43} \right) = \left( { - 3} \right)\) \(x = \left( { - 3} \right) + \left( { - 43} \right)\) \(x = {\rm{\;}} - \left( {3 + 43} \right)\) \(x = {\rm{\;}} - 46.\) Vậy \(x = {\rm{\;}} - 46.\) Đáp án: C Bài 2: Giá trị của \(x\) biết \( - 20 - x = 96\) là: A. 116. B. -76. C. -116. D. 76. Phương pháp Muốn tìm số trừ, ta lấy số bị trừ trừ đi hiệu. Lời giải \(\begin{array}{*{20}{l}}{ - 20 - x = 96}\\{x = {\rm{\;}} - 20 - 96}\\{x = \left( { - 20} \right) + \left( { - 96} \right)}\\{x = {\rm{\;}} - 116}\end{array}\) Vậy \(x = - 116\) Đáp án: C Bài 3: Cho \(25 - \left( {x + 15} \right) = {\rm{\;}} - 415 - \left( { - 215 - 415} \right)\) thì \(x\) bằng A. -205. B. 175. C. -175. D. 205. Phương pháp Tính vế phải Tìm \(x + 15\) Tìm \(x\) Lời giải \(\begin{array}{*{20}{l}}{25 - \left( {x + 15} \right) = {\rm{\;}} - 415 - \left( { - 215 - 415} \right)}\\{25 - \left( {x + 15} \right) = 215}\\{x + 15 = 25 - 215}\\{x + 15 = {\rm{\;}} - 190}\\{x = {\rm{\;}} - 190 - 15}\\{x = {\rm{\;}} - 205}\end{array}\) Vậy \(x = - 205\) Đáp án: A Bài 4: Tìm \(x\) biết \(2\left( {x - 5} \right) - 3\left( {x - 7} \right) = {\rm{\;}} - 2.\) A. \(x = 13\). B. \(x = 5\). C. \(x = 7\). D. \(x = 6\). Phương pháp Áp dụng tính chất của phép nhân để phá ngoặc Thu gọn vế trái Tìm \(x\) Lời giải \(\begin{array}{*{20}{l}}{2\left( {x - 5} \right) - 3\left( {x - 7} \right) = {\rm{\;}} - 2}\\{2x - 10 - 3.x + 3.7 = {\rm{\;}} - 2}\\{2x - 10 - 3x + 21 = {\rm{\;}} - 2}\\{\left( {2x - 3x} \right) + \left( {21 - 10} \right) = {\rm{\;}} - 2}\\{\left( {2 - 3} \right)x + 11 = {\rm{\;}} - 2}\\{ - x + 11 = {\rm{\;}} - 2}\\{ - x = {\rm{\;}} - 2 - 11}\\{ - x = {\rm{\;}} - 13}\\{x = 13}\end{array}\) Vậy \(x = 13\) Đáp án: A Bài 5: Cho \(\left( { - 4} \right).\left( {x - 3} \right) = 20.\) Tìm \(x\). A. 8. B. -5. C. -2. D. 2. Phương pháp + Sử dụng quy tắc nhân hai số nguyên cùng dấu để tìm ra giá trị của \(x - 3\) + Sau đó áp dụng quy tắc chuyển vế và tính chất tổng đại số để tìm \(x\). Lời giải Vì \(\left( { - 4} \right).\left( { - 5} \right) = 4.5 = 20\) nên để \(\left( { - 4} \right).\left( {x - 3} \right) = 20\) thì \(x - 3 = {\rm{\;}} - 5\) Khi đó ta có: \(\begin{array}{*{20}{l}}{x - 3 = {\rm{\;}} - 5}\\{x = {\rm{\;}} - 5 + 3}\\{x = {\rm{\;}} - 2}\end{array}\) Vậy \(x = {\rm{\;}} - 2\). Đáp án: C Bài 6: Tìm x, biết: a) \((x - 125).21 = 0\) b) \((2x - 16):12 = - 8\) c) \((3x - 24).( - 39) = 117\) d) \(123 - (2x - 3) = ( - 118)\) e) \((27 - x).(3x + 9).(42 - 6x) = 0\) Phương pháp Tìm thừa số chưa biết = tích : thừa số đã biết Tìm số bị chia = thương . số chia Tìm số hạng chưa biết = tổng – số hạng đã biết Lời giải a) \((x - 125).21 = 0\) \(x - 125 = 0\) \(x = 125\) Vậy \(x = 125\). b) \((2x - 16):12 = - 8\) \(2x - 16 = ( - 8).12\) \(2x - 16 = - 96\) \(2x = ( - 96) + 16\) \(2x = - 80\) \(x = ( - 80):2\) \(x = - 40\) Vậy \(x = - 40\). c) \((3x - 24).( - 39) = 117\) \(3x - 24 = 117:( - 39)\) \(3x - 24 = - 3\) \(3x = ( - 3) + 24\) \(3x = 21\) \(x = 21:3\) \(x = 7\) Vậy \(x = 7\). d) \(123 - (2x - 3) = ( - 118)\) Cách 1: \(123 - (2x - 3) = ( - 118)\) \(2x - 3 = 123 - ( - 118)\) \(2x - 3 = 123 + 118\) \(2x - 3 = 241\) \(2x = 241 + 3\) \(2x = 244\) \(x = 244:2\) \(x = 122\) Vậy \(x = 122\). Cách 2: \(123 - (2x - 3) = ( - 118)\) \(123 - 2x + 3 = ( - 118)\) \(123 + 3 + 118 = 2x\) \(244 = 2x\) \(x = 244:2\) \(x = 122\) Vậy \(x = 122\). e) \((27 - x).(3x + 9).(42 - 6x) = 0\) \(27 - x = 0\) hoặc \(3x + 9 = 0\) hoặc \(42 - 6x = 0\) TH1: \(27 - x = 0\) \(x = 27 - 0\) \(x = 27\) TH2: \(3x + 9 = 0\) \(3x = 0 - 9\) \(3x = - 9\) \(x = - 9:3\) \(x = - 3\) TH3: \(42 - 6x = 0\) \(6x = 42 - 0\) \(6x = 42\) \(x = 42:6\) \(x = 7\) Vậy \(x \in \{ 27; - 3;7\} \) Bài 7: Tìm \(x\), biết: a) \({(x + 7)^2} = 36\) b) \(2.{(x + 3)^2} - 24 = - 6\) Phương pháp Đưa về dạng: \({A^2} = {B^2}\) thì A = B hoặc A = - B Lời giải a) \({(x + 7)^2} = 36\) \({(x + 7)^2} = {6^2}\) \(x + 7 = 6\) hoặc \(x + 7 = - 6\) TH1: \(x + 7 = 6\) \(x = 6 - 7\) \(x = - 1\) TH2: \(x + 7 = - 6\) \(x = - 6 - 7\) \(x = - 13\) Vậy \(x \in \{ - 1; - 13\} \) b) \(2.{(x + 3)^2} - 24 = - 6\) \(2.{(x + 3)^2} = ( - 6) + 24\) \(2.{(x + 3)^2} = 18\) \({(x + 3)^2} = 9\) \({(x + 3)^2} = {3^2}\) TH1: \(x + 3 = 3\) \(x = 3 - 3\) \(x = 0\) TH2: \(x + 3 = - 3\) \(x = - 3 - 3\) \(x = - 6\) Vậy \(x \in \{ 0; - 6\} \) Bài 8: Tìm số nguyên \(x\), biết: a) \(x - 10 = {\rm{\;}} - 65\) b) \(32:\left( {x + 125} \right) = - {4^2}\) c) \(20 - 5\left( {2 - x} \right) = 45\) d) \(29 \vdots x\). Phương pháp a) Tìm số bị trừ trong một hiệu: x – a = b thì x = b + a b) Tính x + 125. Tìm số hạng chưa biết trong một tổng: a + x = b (hoặc x + a = b) thì x = b – a c) Tính 2 – x. Tìm số trừ trong một hiệu: a – x = b thì x = a – b d) \(29 \vdots x\) nên \(x \in \) Ư(29). Lời giải a) \(x - 10 = {\rm{\;}} - 65\) \(\begin{array}{*{20}{l}}{x = {\rm{\;}} - 65 + 10}\\{x = {\rm{\;}} - 55}\end{array}\) Vậy \(x = {\rm{\;}} - 55\) b) \(32:\left( {x + 125} \right) = {\rm{\;}} - {4^2}\) \(\begin{array}{*{20}{l}}{32:\left( {x + 125} \right) = {\rm{\;}} - 16}\\{x + 125 = 32:\left( { - 16} \right)}\\{x + 125 = {\rm{\;}} - 2}\\{x = {\rm{\;}} - 2 - 125}\\{x = {\rm{\;}} - 127}\end{array}\) Vậy \(x = {\rm{\;}} - 127\) c) \(20 - 5\left( {2 - x} \right) = 45\) \(\begin{array}{*{20}{l}}{5\left( {2 - x} \right) = 20 - 45}\\{5\left( {2 - x} \right) = {\rm{\;}} - 25}\\{2 - x = {\rm{\;}} - 25:5}\\{2 - x = {\rm{\;}} - 5}\\{x = 2 - \left( { - 5} \right)}\\{x = 7}\end{array}\) Vậy \(x = 7\). d) Vì \(29 \vdots x\) nên x là ước của 29. Mà x là số nguyên nên \(x \in \left\{ { - 29; - 1;1;29} \right\}\). Bài 9: Tìm số nguyên x, biết: a) \(x - 42 = \left( { - 18} \right) + \left( { - 16} \right)\) b) \(\left( {5x - 3} \right) + 85 = 32\) c) \(2{\left( {x + 1} \right)^2} + 4 = {2^2}{.3^2}\) d) \(7 \vdots \left( {x - 3} \right)\) Phương pháp a) Tính x – 42. Tìm số bị trừ trong một hiệu: x – a = b thì x = b + a b) Tính 5x – 3. Tính 5x. Tìm thừa số chưa biết trong một tích: a.x = b (hoặc x.a = b) thì x = b : a d) \(7 \vdots \left( {x - 3} \right)\) thì \(\left( {x - 3} \right) \in \) Ư(7) Lời giải a) \(x - 42 = \left( { - 18} \right) + \left( { - 16} \right)\) \(\begin{array}{*{20}{l}}{x - 42 = - 34}\\{x = - 34 + 42}\\{x = 8}\end{array}\) Vậy \(x = 8\) b) \(\left( {5x - 3} \right) + 85 = 32\) \(\begin{array}{*{20}{l}}{5x - 3 = 32 - 85}\\{5x - 3 = - 53}\\{5x = - 53 + 3}\\{5x = - 50}\\{x = - 50:5}\\{x = - 10}\end{array}\) Vậy \(x = - 10\) c) \(2{\left( {x + 1} \right)^2} + 4 = {2^2}{.3^2}\) \(\begin{array}{*{20}{l}}{2{{\left( {x + 1} \right)}^2} + 4 = 4.9}\\{2{{\left( {x + 1} \right)}^2} + 4 = 36}\\{2{{\left( {x + 1} \right)}^2} = 36 - 4}\\{2{{\left( {x + 1} \right)}^2} = 32}\\{{{\left( {x + 1} \right)}^2} = 32:2}\\{{{\left( {x + 1} \right)}^2} = 16}\\{x + 1 = \pm 4}\end{array}\) TH1: \(x + 1 = 4\) suy ra \(x = 4 - 1 = 3\) TH2: \(x + 1 = - 4\) suy ra \(x = - 4 - 1 = - 5\) Vậy \(x \in \left\{ { - 5;3} \right\}\). d) \(7 \vdots \left( {x - 3} \right)\) Suy ra \(\left( {x - 3} \right) \in \) Ư(7) \( = \left\{ { \pm 1; \pm 7} \right\}\) Ta có bảng giá trị: Vậy \(x \in \left\{ {2;4; - 4;10} \right\}\). Bài 10: Tìm số nguyên x, sao cho: a) \(\frac{6}{{x - 2}}\) là số nguyên b) \(\frac{{4x - 3}}{{x + 2}}\) là số nguyên Phương pháp Đưa về dạng \(\frac{k}{A}\) là số nguyên (k là số nguyên đã biết) khi và chỉ khi k chia hết cho A hay A là một Ư(k). Lời giải a) Để \(\frac{6}{{x - 2}}\) là số nguyên thì \(6 \vdots (x - 2)\) Do đó \(x - 2 \in \) Ư\((6) = \{ \pm 1; \pm 2; \pm 3; \pm 6\} \) Ta có bảng sau:
Vậy \(x \in \{ - 4; - 1;0;1;3;4;5;8\} \) b) Ta có: \(\frac{{4x - 3}}{{x + 2}} = \frac{{4.(x + 2) - 11}}{{x + 2}} = 4 - \frac{{11}}{{x + 2}}\) Để \(\frac{{4x - 3}}{{x + 2}}\) là số nguyên thì \(\frac{{11}}{{x + 2}}\) là số nguyên hay \(11 \vdots \left( {x + 2} \right)\) Do đó \(x + 2 \in \) Ư\((11) = \{ \pm 1; \pm 11\} \) Ta có bảng sau:
Vậy \(x \in \{ - 13; - 3; - 1;9\} \)
|





















Danh sách bình luận