Dạng 2. Chứng minh một số là số nguyên tố, hợp số Chủ đề 3 Ôn hè Toán 6Tải vềSố nguyên tố là số tự nhiên khác 0, 1, chỉ có ước là 1 và chính nó. Hợp số là số tự nhiên khác 0, 1, có nhiều hơn 2 ước. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
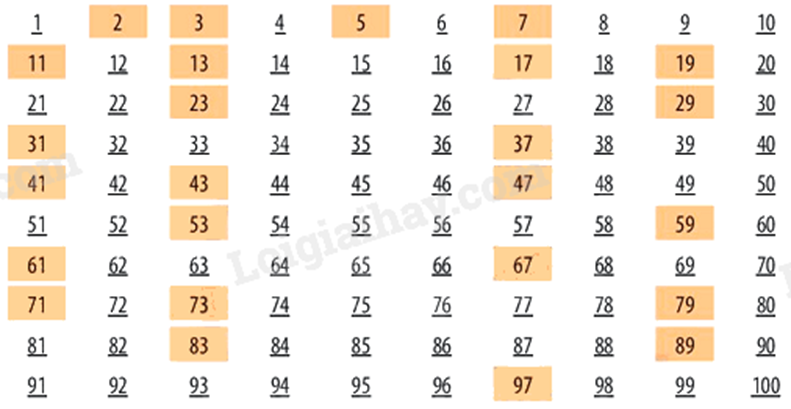
Lý thuyết * Khái niệm - Số nguyên tố là số tự nhiên khác 0, 1, chỉ có 2 ước là 1 và chính nó. - Hợp số là số tự nhiên khác 0, 1, có nhiều hơn 2 ước. * Lưu ý - Số 0 và số 1 không phải là số nguyên tố, cũng không phải là hợp số. - Số 2 là số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất. Như vậy, trừ số 2, mọi số nguyên tố đều là số lẻ. Nhưng ngược lại, một số lẻ chưa chắc là số nguyên tố. - Để khẳng định một số là hợp số, ta thường sử dụng các dấu hiệu chia hết (2,3,5,8,…) để tìm ra 1 ước khác 1 và chính nó. - Những số: 2; 3; 5; 7; 11; 13; 17; 19; 23; … là những số nguyên tố. Có vô số số nguyên tố. * Bảng số nguyên tố nhỏ hơn 100 (HS nên thuộc để nhận diện)
* Dấu hiệu để nhận biết một số nguyên tố Số tự nhiên a không chia hết cho mọi số nguyên tố p với p2 < a thì a là số nguyên tố. Cách nhận biết số nguyên tố Cách 1 Chia số đó lần lượt cho các số nguyên tố từ nhỏ đến lớn: 2; 3; 5; 7... - Nếu có một phép chia hết thì số đó không là số nguyên tố. - Nếu thực hiện phép chia cho đến lúc thương số nhỏ hơn số chia mà các phép chia vẫn có số dư thì số đó là số nguyên tố. Cách 2 - Một số có hai ước số lớn hơn 1 thì số đó không phải là số nguyên tố. - Nếu A là hợp số thì A có ít nhất một ước nguyên tố không vượt quá A. - Với quy tắt trên trong một khoảng thời gian ngắn, với các dấu hiệu chia hết thì ta nhanh chóng trả lời được một số có hai chữ số nào đó là nguyên tố hay không. Bài tập Bài 1: Khẳng định nào sau đây là đúng? A. Số 2 là số nguyên tố chẵn duy nhất. B. Số 0 là số nguyên tố. C. Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9. D. Các số nguyên tố đều là số lẻ. Bài 2: Kết quả của phép tính nào sau đây là số nguyên tố: A. \(15 - 5 + 3\). B. \(7.2 + 1\). C. \(14.6:4\). D. \(6.4 - 12.2\). Bài 3: Thay dấu * để được số nguyên tố \(\overline {3*} \): A. \(7\). B. \(4\). C. \(6\). D. \(9\). Bài 4: Cho các số 21; 77; 71; 101. Chọn câu đúng. A. Số 21 là hợp số, các số còn lại là số nguyên tố. B. Có hai số nguyên tố và hai hợp số trong các số trên. C. Chỉ có một số nguyên tố còn lại là hợp số. D. Không có số nguyên tố nào trong các số trên. Bài 5: Cho \(A = 90.17 + 34.40 + 12.51\) và \(B = 5.7.9 + 2.5.6\) . Chọn câu đúng. A. A là số nguyên tố, B là hợp số. B. A là hợp số, B là số nguyên tố. C. Cả A và B là số nguyên tố. D. Cả A và B đều là hợp số. Bài 6: Chứng minh rằng: a) 2414 + 9218 là hợp số. b) \(\overline {abcabc} + 7\) là hợp số. Bài 7: Cho \(A = 1.3.5.7...13 + 20\) và \(B = 147.247.347 - 13\). Kiểm tra xem A và B là số nguyên tố hay hợp số? Bài 8: Cho nguyên tố \(p\) chia cho 42 có số dư \(r\) là hợp số. Tìm \(r\). Bài 9: Tìm số tự nhiên \(x\) sao cho \(41.x\) là số nguyên tố. Bài 10: Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố. Bài 11: Tìm các số nguyên tố lớn hơn 1990 và nhỏ hơn 2006. Bài 12: Kiểm tra xem số 1021 có là số nguyên tố không? ----HẾT---- Lời giải chi tiết: Bài 1: Khẳng định nào sau đây là đúng? A. Số 2 là số nguyên tố chẵn duy nhất. B. Số 0 là số nguyên tố. C. Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9. D. Các số nguyên tố đều là số lẻ. Phương pháp Dựa vào kiến thức về số nguyên tố. Lời giải Chỉ có số 2 là số nguyên tố chẵn duy nhất nên A là khẳng định đúng. Số 0 không phải số nguyên tố nên B sai. Số 9 có 3 ước là 1; 3; 9. Số 9 không phải số nguyên tố nên C sai. Số 2 là số nguyên tố chẵn nên D sai. Đáp án: A Bài 2: Kết quả của phép tính nào sau đây là số nguyên tố: A. \(15 - 5 + 3\). B. \(7.2 + 1\). C. \(14.6:4\). D. \(6.4 - 12.2\). Phương pháp - Thực hiện phép tính để tìm ra kết quả. - Áp dụng định nghĩa hợp số để tìm ra đáp án đúng. Lời giải \(15 - 5 + 3 = 13\) là số nguyên tố. \(7.2 + 1 = 14 + 1 = 15\), ta thấy 15 có ước 1; 3; 5; 15 nên 15 là hợp số. \(14.6:4 = 84:4 = 21,\) ta thấy 21 có ước 1; 3; 7; 21 nên 21 là hợp số. \(6.4 - 12.2 = 24 - 24 = 0,\) ta thấy \(0\) không là số nguyên tố, không là hợp số. Đáp án: A Bài 3: Thay dấu * để được số nguyên tố \(\overline {3*} \): A. \(7\). B. \(4\). C. \(6\). D. \(9\). Phương pháp - Dấu * có thể nhận các giá trị \(\{ {\rm{7}};{\rm{4}};{\rm{6}};{\rm{9}}\} \) - Dùng định nghĩa số nguyên tố để tìm ra số nguyên tố. Lời giải Đáp án A: Vì 37 chỉ chia hết cho 1 và 37 nên 37 là số nguyên tố, do đó chọn A. Đáp án B: 34 không phải là số nguyên tố (34 chia hết cho \(\left\{ {2;4; \ldots } \right\}\)). Do đó loại B. Đáp án C: 36 không phải là số nguyên tố (36 chia hết cho \(\left\{ {1;{\mkern 1mu} {\mkern 1mu} 2;{\rm{3}};{\mkern 1mu} ...;{\mkern 1mu} {\rm{36}}} \right\}\)). Do đó loại C. Đáp án D: 39 không phải là số nguyên tố (39 chia hết cho \(\left\{ {1;{\mkern 1mu} {\mkern 1mu} 3;...{\mkern 1mu} ;{\mkern 1mu} 39} \right\})\). Do đó loại D. Đáp án: A Bài 4: Cho các số 21; 77; 71; 101. Chọn câu đúng. A. Số 21 là hợp số, các số còn lại là số nguyên tố. B. Có hai số nguyên tố và hai hợp số trong các số trên. C. Chỉ có một số nguyên tố còn lại là hợp số. D. Không có số nguyên tố nào trong các số trên. Phương pháp + Tìm các ước của các số 21; 77; 71; 101 + Dùng định nghĩa số nguyên tố và hợp số để tìm các số nguyên tố và hợp số Lời giải + Số 21 có các ước 1; 3; 7; 21 nên 21 là hợp số. + Số 77 có các ước 1; 7; 11; 77 nên 77 là hợp số. + Số 71 chỉ có hai ước là 1; 71 nên 71 là số nguyên tố. + Số 101 chỉ có hai ước là 1; 101 nên 101 là số nguyên tố. Như vậy có hai số nguyên tố là 71; 101 và hai hợp số là 21; 77. Đáp án: B Bài 5: Cho \(A = 90.17 + 34.40 + 12.51\) và \(B = 5.7.9 + 2.5.6\) . Chọn câu đúng. A. A là số nguyên tố, B là hợp số. B. A là hợp số, B là số nguyên tố. C. Cả A và B là số nguyên tố. D. Cả A và B đều là hợp số. Phương pháp + Dựa vào tính chia hết của một tổng để xét xem A, B có chia hết cho số nào khác \(1\) hay không? + Sử dụng định nghĩa số nguyên tố và hợp số để xác định xem A, B là số nguyên tố hay hợp số. Lời giải +) Ta có \(A = 90.17 + 34.40 + 12.51\) Vì \(17{\mkern 1mu} \vdots {\mkern 1mu} 17;{\mkern 1mu} 34{\mkern 1mu} \vdots {\mkern 1mu} {\rm{\;}}17;51{\mkern 1mu} \vdots {\mkern 1mu} 17\) nên \(A = 90.17 + 34.40 + 12.51\) chia hết cho 17 nên ngoài ước là \(1\) và chính nó thì \(A\) còn có ước là 17. Do đó \(A\) là hợp số. +) Ta có \(B = 5.7.9 + 2.5.6 = 5.\left( {7.9 + 2.6} \right){\mkern 1mu} \vdots {\mkern 1mu} 5\) nên \(B = 5.7.9 + 2.5.6\) ngoài ước là \(1\) và chính nó thì \(A\) còn có ước là \(5\). Do đó \(B\) là hợp số. Vậy cả \(A\) và \(B\) đều là hợp số. Đáp án: D Bài 6: Chứng minh rằng: a) 2414 + 9218 là hợp số. b) \(\overline {abcabc} + 7\) là hợp số. Phương pháp Nếu a\( \vdots \)m; b\( \vdots \)m thì (a + b) \( \vdots \) m Lời giải a) Vì 2414 \( \vdots \) 2; 9218 \( \vdots \) 2 nên (2414 + 9218) \( \vdots \) 2 Do đó, 2414 + 9218 có nhiều hơn 2 ước nên là hợp số. b) Ta có: \(\begin{array}{l}\overline {abcabc} + 7\\ = 1000.\overline {abc} + \overline {abc} + 7\\ = 1001.\overline {abc} + 7\end{array}\) Vì 1001 \( \vdots \) 7 nên 1001 . \(\overline {abc} \) \( \vdots \) 7 Mà 7 \( \vdots \) 7 Do đó, \((1001.\overline {abc} + 7) \vdots 7\) Vậy \(\overline {abcabc} + 7\) có nhiều hơn 2 ước nên là hợp số. Bài 7: Cho \(A = 1.3.5.7...13 + 20\) và \(B = 147.247.347 - 13\). Kiểm tra xem A và B là số nguyên tố hay hợp số? Phương pháp + Dựa vào tính chia hết của một tổng/hiệu để xét xem A, B có chia hết cho số nào khác \(1\) hay không? + Sử dụng định nghĩa số nguyên tố và hợp số để xác định xem A, B là số nguyên tố hay hợp số. Lời giải +) \(A = 1.3.5.7...13 + 20\) Vì \(5 \vdots 5\) nên \(\left( {1.3.5.7...13} \right) \vdots 5\) Mà \(20 \vdots 5\) nên \(\left( {1.3.5.7...13 + 20} \right) \vdots 5\) (tính chất chia hết của một tổng) Do đó \(A = 1.3.5.7...13 + 20\) chia hết cho \(5\) Vì vậy ngoài ước là \(1\) và chính nó thì \(A\) còn có ước là \(5\). Do đó \(A\) là hợp số. +) \(B = 147.247.347 - 13\) Vì \(247 \vdots 13\) nên \(\left( {147.247.347} \right) \vdots 13\) Mà \(13 \vdots 13\) nên \(\left( {147.247.347 - 13} \right) \vdots 13\) (tính chất chia hết của một hiệu) Do đó \(B = 147.247.347 - 13\) chia hết cho \(13\) Vì vậy ngoài ước là \(1\) và chính nó thì \(B\) còn có ước là \(13\). Do đó \(B\) là hợp số. Vậy cả \(A\) và \(B\) đều là hợp số. Bài 8: Cho nguyên tố \(p\) chia cho 42 có số dư \(r\) là hợp số. Tìm \(r\). Phương pháp + Biểu diễn số nguyên tố \(p\) theo số chia 42 và thương \(r\). + Dựa vào định nghĩa số nguyên tố để lập luận và tìm các giá trị \(r\) thỏa mãn. Lời giải Ta có: 42 = 2.3.7. Vì \(p\) là số nguyên tố nên \(r\) không chia hết cho 2; 3; 7. Các hợp số nhỏ hơn 42 không chia hết cho \(2\) là 9; 15; 21; 25; 27; 33; 35; 39 Loại bỏ các số chia hết cho \(3\) và \(7\) ta còn số 25. Vậy \(r = 25\). Bài 9: Tìm số tự nhiên \(x\) sao cho \(41.x\) là số nguyên tố. Phương pháp Xét các trường hợp của \(x\) để \(41.x\) chỉ có 2 ước là 1 và chính nó. Lời giải +) Nếu \(x = 0\) thì \(41.x = 0\) không là số nguyên tố (Loại) +) Nếu \(x = 1\) thì \(41.1 = 41\) là số nguyên tố (Thỏa mãn) +) Nếu x \( \ge \) 2 thì \(41.x\) nhận 1; 41; \(x\); 41.\(x\) làm ước của nó nên là hợp số (Loại) Vậy với \(x = 1\) thì \(41.x\) là số nguyên tố. Bài 10: Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố. Phương pháp + Phân tích \({n^2} + 12n = n\left( {n + 12} \right)\) + Dựa vào định nghĩa số nguyên tố để lập luận và suy ra các giá trị của \(n\). Lời giải Ta có \({n^2} + 12n = n\left( {n + 12} \right);{\mkern 1mu} n + 12 > 1\) nên \({n^2} + 12n\) có ít nhất hai ước là n và \(n + 12\). Mà \({n^2} + 12n\) là số nguyên tố nên \({n^2} + 12n\) chỉ có ước là 1 và chính nó. Do vậy \(n = 1\), khi đó \({n^2} + 12n = n + 12\). Thử lại: \({n^2} + 12n = {1^2} + 12.1 = 13\) (là số nguyên tố) Vậy với \(n = 1\) thì \({n^2} + 12n\) là số nguyên tố. Bài 11: Tìm các số nguyên tố lớn hơn 1990 và nhỏ hơn 2006. Phương pháp Số tự nhiên a không chia hết cho mọi số nguyên tố p với p2 < a thì a là số nguyên tố. Lời giải +) Ta loại bỏ các số chia hết cho 2: 1992; 1994; 1996; 1998; 2000; 2002; 2004. +) Trong các số còn lại, ta loại bỏ các số chia hết cho 3: 1995; 2001 +) Ta còn cần xét các số 1991; 1993; 1997; 1999; 2003. Các số nguyên tố p với p2 < 2005 là: 2;3;5;7;9;11;13;17;19;23;29;31;37;41;43.
Vậy các số nguyên tố lớn hơn 1990 và nhỏ hơn 2006 là: 1993; 1997; 1999; 2003. Bài 12: Kiểm tra xem số 1021 có là số nguyên tố không? Phương pháp Số tự nhiên a không chia hết cho mọi số nguyên tố p với p2 < a thì a là số nguyên tố. Lời giải Các số nguyên tố p với p2 < 1021 là: 2;3;5;7;9;11;13;17;19;23;29;31. Số 1021 không chia hết cho số p nào ở trên. Do đó, số 1021 là số nguyên tố.
|




















Danh sách bình luận