Trắc nghiệm Bài 3. Chuyển động đều - Chuyển động không đều - Vật Lí 8Đề bài
Câu 1 :
Thả viên bi trên máng nghiêng và máng ngang như hình vẽ. 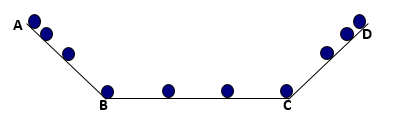 Phát biểu nào dưới đây chưa chính xác
Câu 2 :
Công thức tính vận tốc trung bình trên quãng đường gồm 2 đoạn \({s_1}\) và \({s_2}\) là:
Câu 3 :
Trong các chuyển động sau, chuyển động nào là đều
Câu 4 :
Đào đi bộ từ nhà tới trường, quãng đường đầu dài \(200m\) Đào đi mất \(1\) phút \(40\) giây; quãng đường còn lại dài \(300m\) Đào đi mất \(100\) giây. Vận tốc trung bình của Đào trên mỗi đoạn đường và cả đoạn đường lần lượt là:
Câu 5 :
Tàu Thống Nhất TN1 đi từ ga Huế vào ga Sài Gòn mất \(20h\). Biết vận tốc trung bình của tàu là \(15m/s\). Hỏi chiều dài của đường ray từ Huế vào Sài Gòn là bao nhiêu?
Câu 6 :
Trong trận đấu giữa Đức và Áo ở EURO 2008, Tiền vệ Mai-Cơn BaLack của đội tuyển Đức sút phạt cách khung thành của đội Áo \(30m\). Các chuyên gia tính được vận tốc trung bình của quả đá phạt đó lên tới \(108km/h\). Hỏi thời gian bóng bay từ chân cầu thủ đến khung thành là bao nhiêu?
Câu 7 :
Hưng đạp xe lên dốc dài \(100m\) với vận tốc \(2m/s\), sau đó xuống dốc dài \(140m\) hết \(30s\). Hỏi vận tốc trung bình của Hưng trên cả đoạn đường dốc?
Câu 8 :
Một học sinh vô địch trong giải điền kinh ở nội dung chạy cự li \(1000m\) với thời gian là \(2\) phút \(5\) giây. Vận tốc của học sinh đó là:
Câu 9 :
Một người đi xe đạp trên đoạn đường \(MNPQ\). Biết trên đoạn đường \(MN = {s_1}\) người đó đi với vận tốc \({v_1}\), trong thời gian \({t_1}\); trên đoạn đường \(NP = {s_2}\) người đó đi với vận tốc \({v_2}\), trong thời gian \({t_2}\); trên đoạn đường \(PQ = {s_3}\) người đó đi với vận tốc \({v_3}\), trong thời gian \({t_3}\). Vận tốc trung bình của người đó trên đoạn đường \(MNPQ\) được tính bởi công thức:
Câu 10 :
Một xe máy di chuyển giữa hai địa điểm A và B. Vận tốc trong \(1/2\) thời gian đầu là \(30km/h\) và trong \(1/2\) thời gian sau là \(15m/s\). Vận tốc trung bình của ô tô trên cả đoạn đường là:
Câu 11 :
Một người đi xe máy trên đoạn đường \(ABC\). Biết trên đoạn đường \(AB\) người đó đi với vận tốc \(16km/h\), trong thời gian \({t_1} = 15\) phút; trên đoạn đường \(BC\) người đó đi với vận tốc \(24km/h\), trong thời gian \({t_2} = 25\) phút. Vận tốc trung bình của người đó trên đoạn đường \(ABC\) là:
Câu 12 :
Give the correct form of the verbs in the brackets to complete the sentences He (write) a book since he (be) a child.
Câu 13 :
Bắn một viên bi lên một máng nghiêng, sau đó viên bi lăn xuống với vận tốc \(6{\rm{ }}cm/s\). Biết vận tốc trung bình của viên bi cả đi lên và đi xuống là \(4{\rm{ }}cm/s\). Hỏi vận tốc của viên bi khi đi lên?
Câu 14 :
Hai bến sông A và B cách nhau \(24{\rm{ }}km\), dòng nước chảy đều theo hướng \(A\) đến \(B\) với vận tốc \(6km/h\). Một canô đi từ A đến B mất \(1h\). Cũng với canô đó đi ngược dòng mất bao lâu? Biết công suất máy của canô là không đổi.
Câu 15 :
Xe đạp và xe máy khởi hành cùng một lúc, chạy cùng chiều trên đoạn đường AB. Hai xe có đồ thị đường đi như hình vẽ. 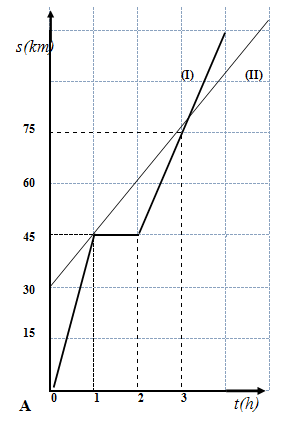 (I) - ứng với xe máy (II) - ứng với xe đạp Từ đồ thị, hãy cho biết khoảng thời gian từ lúc khởi hành đến khi hai xe gặp nhau lần thứ nhất và vị trí lúc hai xe gặp nhau lúc đó cách A bao nhiêu?
Hai chiếc xe ô tô chuyên động trên một đường thẳng có đồ thị đường đi được biểu diễn như hình sau: 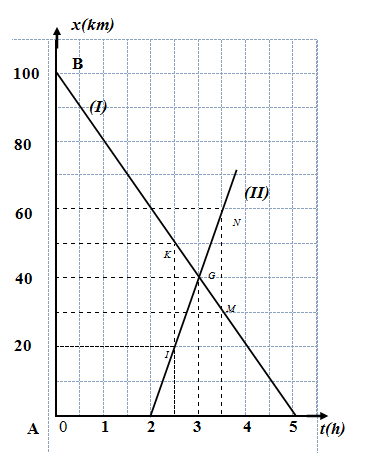 Câu 16
Nhận xét về thời điểm xuất phát của hai xe:
Câu 17
Thời điểm và vị trí của hai xe so với điểm A khi chúng gặp nhau.
Câu 18
Thời điểm của hai xe khi chúng cách nhau 30km
Câu 19 :
Một người đi xe đạp trên một đoạn đường thẳng AB. Trên \(1/3\) đoạn đường đầu đi với vận tốcc \(14km/h\), \(1/3\) đoạn đường tiếp theo đi với vận tốc \(16km/h\) , \(1/3\) đoạn đường cuối đi với vận tốc \(8km/h\). Vận tốc trung bình của xe đạp trên cả đoạn đường AB có thể nhận giá trị nào? Hãy chọn câu đúng
Câu 20 :
Một người đi xe máy từ A đến B. Trên đoạn đường đầu người đó đi hết 15 phút. Đoạn đường còn lại người đó đi trong thời gian 30 phút với vận tốc 12m/s. Hỏi đoạn đường đầu dài bao nhiêu? Biết vận tốc trung bình của người đó trên cả quãng đường AB là 36km/h. Hãy chọn câu trả lời đúng.
Câu 21 :
Hai ô tô chuyển động thẳng đều khởi hành đồng thời ở 2 địa điểm cách nhau 20km. Nếu đi ngược chiều thi sau 15 phút chúng gặp nhau. Nếu đi cùng chiều sau 30 phút thì chúng đuổi kịp nhau. Vận tốc của hai xe đó là:
Câu 22 :
Một người đi xe máy với vận tốc 12m/s trong thời gian 20 phút. Quãng đường người đó đi được là
Câu 23 :
Một học sinh đi xe đạp từ nhà tới trường với vận tốc 12km/h mất thời gian 15 phút. Quãng đường từ nhà tới trường là:
Câu 24 :
Hai người cùng đi từ A đến B. Người thứ nhất đi xe đạp với vận tốc 4m/s, người thứ hai đi xe máy với vận tốc 36km/h. Quãng đường từ A đến B là 7,2 km. Hỏi người thứ hai phải xuất phát tại A lúc mấy giờ để hai người đến B cùng một lúc. Biết người thứ nhất khởi hành tại A lúc 6h.
Lời giải và đáp án
Câu 1 :
Thả viên bi trên máng nghiêng và máng ngang như hình vẽ.  Phát biểu nào dưới đây chưa chính xác
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C - sai vì: Viên bị chuyển động nhanh dần từ \(A \to B\) và chuyển động chậm dần từ \(B \to C\)
Câu 2 :
Công thức tính vận tốc trung bình trên quãng đường gồm 2 đoạn \({s_1}\) và \({s_2}\) là:
Đáp án : D Lời giải chi tiết :
\({v_{tb}} = \frac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Trong đó \({s_1},{s_2},...,{s_n}\) và \({t_1},{t_2},...,{t_n}\) là những quãng đường và thời gian để đi hết quãng đường đó.
Câu 3 :
Trong các chuyển động sau, chuyển động nào là đều
Đáp án : B Lời giải chi tiết :
A, C, D - chuyển động không đều B - chuyển động đều
Câu 4 :
Đào đi bộ từ nhà tới trường, quãng đường đầu dài \(200m\) Đào đi mất \(1\) phút \(40\) giây; quãng đường còn lại dài \(300m\) Đào đi mất \(100\) giây. Vận tốc trung bình của Đào trên mỗi đoạn đường và cả đoạn đường lần lượt là:
Đáp án : A Phương pháp giải :
Áp dụng biểu thức tính vận tốc trung bình: \({v_{tb}} = \frac{s}{t}\) Lời giải chi tiết :
+ Vận tốc trung bình trên đoạn đường thứ nhất: \({v_{t{b_1}}} = \frac{{{s_1}}}{{{t_1}}} = \frac{{200}}{{60 + 40}} = 2m/s\) + Vận tốc trung bình trên đoạn đường thứ hai: \({v_{t{b_2}}} = \frac{{{s_2}}}{{{t_2}}} = \frac{{300}}{{100}} = 3m/s\) + Vận tốc trung bình trên cả đoạn đường là: \({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{200 + 300}}{{100 + 100}} = 2,5m/s\)
Câu 5 :
Tàu Thống Nhất TN1 đi từ ga Huế vào ga Sài Gòn mất \(20h\). Biết vận tốc trung bình của tàu là \(15m/s\). Hỏi chiều dài của đường ray từ Huế vào Sài Gòn là bao nhiêu?
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính vận tốc trung bình: \({v_{tb}} = \frac{s}{t}\) Lời giải chi tiết :
Ta có: \({v_{tb}} = \frac{s}{t} \to s = {v_{tb}}t = 15.\left( {20.60.60} \right) = 1080000m = 1080km\)
Câu 6 :
Trong trận đấu giữa Đức và Áo ở EURO 2008, Tiền vệ Mai-Cơn BaLack của đội tuyển Đức sút phạt cách khung thành của đội Áo \(30m\). Các chuyên gia tính được vận tốc trung bình của quả đá phạt đó lên tới \(108km/h\). Hỏi thời gian bóng bay từ chân cầu thủ đến khung thành là bao nhiêu?
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính vận tốc trung bình: \({v_{tb}} = \frac{s}{t}\) Lời giải chi tiết :
Đổi đơn vị: \(108km/h = 30m/s\) Ta có: \({v_{tb}} = \frac{s}{t} \to t = \frac{s}{{{v_{tb}}}} = \frac{{30}}{{30}} = 1{\rm{s}}\)
Câu 7 :
Hưng đạp xe lên dốc dài \(100m\) với vận tốc \(2m/s\), sau đó xuống dốc dài \(140m\) hết \(30s\). Hỏi vận tốc trung bình của Hưng trên cả đoạn đường dốc?
Đáp án : D Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \frac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
+ Thời gian Hưng đạp xe lên dốc là: \({t_1} = \frac{{{s_1}}}{{{v_1}}} = \frac{{100}}{2} = 50{\rm{s}}\) + Vận tốc trung bình của Hưng trên cả đoạn đường dốc là: \({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{100 + 140}}{{50 + 30}} = 3m/s\)
Câu 8 :
Một học sinh vô địch trong giải điền kinh ở nội dung chạy cự li \(1000m\) với thời gian là \(2\) phút \(5\) giây. Vận tốc của học sinh đó là:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính vận tốc trung bình: \({v_{tb}} = \dfrac{s}{t}\) Lời giải chi tiết :
Ta có, + Thời gian học sinh đó chạy \(1000m\) là: \(t = 2.60 + 5 = 125{\rm{s}}\) + Vận tốc của học sinh đó là: \({v_{tb}} = \dfrac{s}{t} = \dfrac{{1000}}{{125}} = 8m/s\)
Câu 9 :
Một người đi xe đạp trên đoạn đường \(MNPQ\). Biết trên đoạn đường \(MN = {s_1}\) người đó đi với vận tốc \({v_1}\), trong thời gian \({t_1}\); trên đoạn đường \(NP = {s_2}\) người đó đi với vận tốc \({v_2}\), trong thời gian \({t_2}\); trên đoạn đường \(PQ = {s_3}\) người đó đi với vận tốc \({v_3}\), trong thời gian \({t_3}\). Vận tốc trung bình của người đó trên đoạn đường \(MNPQ\) được tính bởi công thức:
Đáp án : B Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \dfrac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
Vận tốc trung bình người đi xe đạp đó là: \({v_{tb}} = \dfrac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2} + {t_3}}}\)
Câu 10 :
Một xe máy di chuyển giữa hai địa điểm A và B. Vận tốc trong \(1/2\) thời gian đầu là \(30km/h\) và trong \(1/2\) thời gian sau là \(15m/s\). Vận tốc trung bình của ô tô trên cả đoạn đường là:
Đáp án : A Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \dfrac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
Đổi đơn vị: \(15m/s = 54km/h\) Gọi quãng đường vật đi được trong \(1/2\) thời gian đầu và \(1/2\) thời gian sau lần lượt là: \({s_1},{s_2}\) Ta có: \(\left\{ \begin{array}{l}{s_1} = {v_1}{t_1} = 30\dfrac{t}{2}\\{s_2} = {v_2}{t_2} = 54\dfrac{t}{2}\end{array} \right. \to {s_2} = \dfrac{{54}}{{30}}{s_1} = 1,8{{\rm{s}}_1}\) Vận tốc của ô tô trên cả đoạn đường: \({v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{{{\rm{s}}_1} + 1,8{s_1}}}{t} = \dfrac{{2,8.30\dfrac{t}{2}}}{t} = 42km/h\)
Câu 11 :
Một người đi xe máy trên đoạn đường \(ABC\). Biết trên đoạn đường \(AB\) người đó đi với vận tốc \(16km/h\), trong thời gian \({t_1} = 15\) phút; trên đoạn đường \(BC\) người đó đi với vận tốc \(24km/h\), trong thời gian \({t_2} = 25\) phút. Vận tốc trung bình của người đó trên đoạn đường \(ABC\) là:
Đáp án : C Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \frac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}{t_1} = 15ph = \frac{1}{4}h\\{t_2} = 25ph = \frac{5}{{12}}h\end{array} \right.\) + Quãng đường AB: \(AB = {s_1} = {v_1}{t_1} = 16.\frac{1}{4} = 4km\) + Quãng đường BC: \(BC = {s_2} = {v_2}{t_2} = 24.\frac{5}{{12}} = 10km\) Vận tốc trung bình trên đoạn đường \(ABC\) là : \({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{4 + 10}}{{\frac{1}{4} + \frac{5}{{12}}}} = 21km/h\)
Câu 12 :
Give the correct form of the verbs in the brackets to complete the sentences He (write) a book since he (be) a child. Đáp án
He (write) a book since he (be) a child. Phương pháp giải :
Công thức: S + have/has + Ved/V3 since S + Ved/V2 Lời giải chi tiết :
Công thức: S1 + have/has + Ved/V3 since S2 + Ved/V2 He has written a book since he was a child. (Anh ấy đã viết quyển sách này kể từ khi anh ấy còn là 1 đứa trẻ.)
Câu 13 :
Bắn một viên bi lên một máng nghiêng, sau đó viên bi lăn xuống với vận tốc \(6{\rm{ }}cm/s\). Biết vận tốc trung bình của viên bi cả đi lên và đi xuống là \(4{\rm{ }}cm/s\). Hỏi vận tốc của viên bi khi đi lên?
Đáp án : A Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \frac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
Gọi \({v_1},{v_2}\) lần lượt là vận tốc của bi trên khi đi lên và lăn xuống \({t_1},{t_2}\) lần lượt là thời gian của bi trên khi đi lên và lăn xuống Ta có: \({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{2{\rm{s}}}}{{{t_1} + {t_2}}}{\rm{ }}\left( 1 \right)\) Mặt khác, ta có: \(\left\{ \begin{array}{l}{t_1} = \frac{s}{{{v_1}}}\\{t_2} = \frac{s}{{{v_2}}}\end{array} \right.\) Thay vào \(\left( 1 \right)\) ta được: \(\begin{array}{l}{v_{tb}} = \frac{{2{\rm{s}}}}{{\frac{s}{{{v_1}}} + \frac{s}{{{v_2}}}}}\\ \leftrightarrow 4 = \frac{2}{{\frac{1}{{{v_1}}} + \frac{1}{6}}}\\ \to {v_1} = 3cm/s\end{array}\)
Câu 14 :
Hai bến sông A và B cách nhau \(24{\rm{ }}km\), dòng nước chảy đều theo hướng \(A\) đến \(B\) với vận tốc \(6km/h\). Một canô đi từ A đến B mất \(1h\). Cũng với canô đó đi ngược dòng mất bao lâu? Biết công suất máy của canô là không đổi.
Đáp án : C Phương pháp giải :
Sử dụng biểu thức tính vận tốc: \(v = \frac{s}{t}\) Lời giải chi tiết :
Gọi vận tốc của canô khi dòng nước không chảy là: \({V_{can{\rm{o}}}}\) Vận tốc của canô + vận tốc dòng chảy bằng: $\dfrac{{AB}}{t} = \dfrac{{24}}{1} = 24km/h$ Ta có: Khi canô xuôi dòng: \({V_{can{\rm{o}}}} + 6 = 24\) \( \to {V_{can{\rm{o}}}} = 18km/h\) Khi ngược dòng, thời gian canô phải đi là: \(t = \dfrac{{24}}{{18 - 6}} = 2h\)
Câu 15 :
Xe đạp và xe máy khởi hành cùng một lúc, chạy cùng chiều trên đoạn đường AB. Hai xe có đồ thị đường đi như hình vẽ.  (I) - ứng với xe máy (II) - ứng với xe đạp Từ đồ thị, hãy cho biết khoảng thời gian từ lúc khởi hành đến khi hai xe gặp nhau lần thứ nhất và vị trí lúc hai xe gặp nhau lúc đó cách A bao nhiêu?
Đáp án : A Lời giải chi tiết :
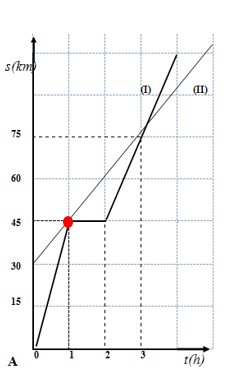 Từ đồ thị ta có, Từ lúc khởi hành, sau 1 giờ xe hai xe gặp nhau lần thứ nhất tại vị trí cách điểm A 45km Hai chiếc xe ô tô chuyên động trên một đường thẳng có đồ thị đường đi được biểu diễn như hình sau:  Câu 16
Nhận xét về thời điểm xuất phát của hai xe:
Đáp án : C Lời giải chi tiết :
Từ đồ thị, ta thấy hai xe xuất phát từ các thời điểm khác nhau Xe (I) xuất phát trước xe (II) 2 giờ Câu 17
Thời điểm và vị trí của hai xe so với điểm A khi chúng gặp nhau.
Đáp án : A Lời giải chi tiết :
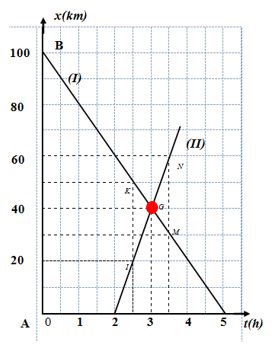 Tọa độ giao điểm của hai đồ thị cho biết: - Hai xe gặp nhau sau $3h$ kể từ khi xe (I) khởi hành từ $B$, sau $1h$ kể từ khi xe (II) khởi hành từ $A$ - Vị trí gặp cách $A$: $40km$. Câu 18
Thời điểm của hai xe khi chúng cách nhau 30km
Đáp án : D Lời giải chi tiết :
Thời điểm và vị trí hai xe cách nhau $30km$: Từ thời điểm \(t = 2,5h\) kẻ đường thẳng song song với trục tung cắt hai đồ thị tại hai điểm $I$ và $K$, tung độ của $I$ là \({x_2} = 20km\) , của K là \({x_1} = 50km\). Vậy hai xe cách nhau \(l = {x_1} - {x_2} = 50 - 20 = 30km\) Xét tương tự với thời điểm \(t = 3,5h\), ta cũng có hai xe cách nhau \(30km\)
Câu 19 :
Một người đi xe đạp trên một đoạn đường thẳng AB. Trên \(1/3\) đoạn đường đầu đi với vận tốcc \(14km/h\), \(1/3\) đoạn đường tiếp theo đi với vận tốc \(16km/h\) , \(1/3\) đoạn đường cuối đi với vận tốc \(8km/h\). Vận tốc trung bình của xe đạp trên cả đoạn đường AB có thể nhận giá trị nào? Hãy chọn câu đúng
Đáp án : B Phương pháp giải :
Sử dụng biểu thức tính vận tốc trung bình của chuyển động không đều: \({v_{tb}} = \dfrac{{{s_1} + {s_2} + ... + {s_n}}}{{{t_1} + {t_2} + ... + {t_n}}}\) Lời giải chi tiết :
Gọi thời gian vật đi được trong từng quãng đường lần lượt là: \({t_1},{t_2},{t_3}\) Ta có: \(\dfrac{{s/3}}{{{v_3}}}\left\{ \begin{array}{l}{t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{s/3}}{{{v_1}}}\\{t_2} = \dfrac{{{s_2}}}{{{v_2}}} = \dfrac{{s/3}}{{{v_2}}}\\{t_3} = \dfrac{{{s_3}}}{{{v_3}}} = \dfrac{{s/3}}{{{v_3}}}\end{array} \right.\) Vận tốc của ô tô trên cả đoạn đường: \({v_{tb}} = \dfrac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2} + {t_3}}} = \dfrac{{s/3 + s/3 + s/3}}{{\dfrac{{s/3}}{{{v_1}}} + \dfrac{{s/3}}{{{v_2}}} + \dfrac{{s/3}}{{{v_3}}}}} \\= \dfrac{1}{{\dfrac{{1/3}}{{14}} + \dfrac{{1/3}}{{16}} + \dfrac{{1/3}}{8}}} = 11,6km/h\)
Câu 20 :
Một người đi xe máy từ A đến B. Trên đoạn đường đầu người đó đi hết 15 phút. Đoạn đường còn lại người đó đi trong thời gian 30 phút với vận tốc 12m/s. Hỏi đoạn đường đầu dài bao nhiêu? Biết vận tốc trung bình của người đó trên cả quãng đường AB là 36km/h. Hãy chọn câu trả lời đúng.
Đáp án : B Phương pháp giải :
Công thức tính vận tốc: \(v = \dfrac{S}{t} \Rightarrow S = v.t\) Vận tốc trung bình: \({v_{tb}} = \dfrac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\) Lời giải chi tiết :
Thời gian đi từ A đến B: \(t = {t_1} + {t_2} = 45phut = \dfrac{3}{4}\,\left( h \right)\) Độ dài AB : \(S = {v_{tb}}.t = 36.\dfrac{3}{4} = 27km\) Độ dài của đoạn đường sau là : \({S_2} = {v_2}.{t_2} = 12.30.60 = 21600m = 21,6km\) Độ dài đoạn đường đầu là : \({S_1} = S - {S_2} = 27 - 21,6 = 5,4km\)
Câu 21 :
Hai ô tô chuyển động thẳng đều khởi hành đồng thời ở 2 địa điểm cách nhau 20km. Nếu đi ngược chiều thi sau 15 phút chúng gặp nhau. Nếu đi cùng chiều sau 30 phút thì chúng đuổi kịp nhau. Vận tốc của hai xe đó là:
Đáp án : D Phương pháp giải :
Phương pháp: Công thức liên hệ giữa quãng đường, vận tốc và thời gian là: S = v.t Lời giải chi tiết :
Cách giải: Gọi v1 và v2 là vận tốc của hai ô tô - Hai ô tô chuyển động ngược chiều đến gặp nhau tại C Ta có: \(\left\{ \begin{array}{l}{s_1} = AC = {v_1}t = {v_1}.0,25\,\,\left( {km} \right)\\{s_2} = BC = {v_2}t = {v_2}.0,25\,\,\left( {km} \right)\end{array} \right.\) Có: \(AB + BC = AB \Leftrightarrow 0,25{v_1} + 0,25{v_2} = 20\,\,\,\,\left( 1 \right)\) - Hai ô tô chuyển động cùng chiều (v1 > v2)
Ta có: \(\left\{ \begin{array}{l}{s_1} = AC = {v_1}t = {v_1}.0,5\,\,\left( {km} \right)\\{s_2} = BC = {v_2}t = {v_2}.0,5\,\,\left( {km} \right)\end{array} \right.\) Có: \(AC - BC = AB \Leftrightarrow 0,5{v_1} - 0,5{v_2} = 20\,\,\,\,\left( 2 \right)\) - Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}0,25{v_1} + 0,25{v_2} = 20\\0,5{v_1} - 0,5{v_2} = 20\,\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{v_1} = 60km/s\\{v_2} = 20km/h\end{array} \right.\)
Câu 22 :
Một người đi xe máy với vận tốc 12m/s trong thời gian 20 phút. Quãng đường người đó đi được là
Đáp án : A Phương pháp giải :
Quãng đường: \(s = v.t\) Lời giải chi tiết :
Đổi: 20 phút = 1200s Quãng đường người đó đi được là: \(s = v.t = 12.1200 = 14400{\mkern 1mu} {\mkern 1mu} \left( m \right) = 14,4{\mkern 1mu} {\mkern 1mu} \left( {km} \right)\)
Câu 23 :
Một học sinh đi xe đạp từ nhà tới trường với vận tốc 12km/h mất thời gian 15 phút. Quãng đường từ nhà tới trường là:
Đáp án : B Phương pháp giải :
Quãng đường: s = v.t Lời giải chi tiết :
Đổi 15 phút \( = \frac{1}{4}\) giờ. Quãng đường từ nhà tới trường là: \(s = v.t = 12.\frac{1}{4} = 3\left( {km} \right)\)
Câu 24 :
Hai người cùng đi từ A đến B. Người thứ nhất đi xe đạp với vận tốc 4m/s, người thứ hai đi xe máy với vận tốc 36km/h. Quãng đường từ A đến B là 7,2 km. Hỏi người thứ hai phải xuất phát tại A lúc mấy giờ để hai người đến B cùng một lúc. Biết người thứ nhất khởi hành tại A lúc 6h.
Đáp án : A Phương pháp giải :
Vận tốc chuyển động: \(v = \frac{S}{t}\) Lời giải chi tiết :
Đổi: 4m/s = 14,4 km/h Thời gian đi từ A đến B của người thứ nhất là: \({t_1} = \frac{S}{{{v_1}}} = \frac{{7,2}}{{14,4}} = 0,5\left( h \right)\) Thời gian đi từ A đến B của người thứ hai là: \({t_2} = \frac{S}{{{v_2}}} = \frac{{7,2}}{{36}} = 0,2\left( h \right)\) Giả sử người thứ 2 xuất phát sau người thứ nhất khoảng thời gian là t Để 2 người đến B cùng lúc thì người thứ 2 xuất phát trước người thứ nhất là: \({t_2} + t = {t_1} \Rightarrow t = {t_1} - {t_2} = 0,5 - 0,2 = 0,3\left( h \right) = 18{\mkern 1mu} {\mkern 1mu} \left( {phut} \right)\) Vậy người thứ hai xuất phát lúc 6 giờ 18 phút
|






















Danh sách bình luận