Trắc nghiệm Bài 4. Chuyển động biến đổi - Vật Lí 10 Cánh diềuĐề bài
Câu 1 :
Câu nào dưới đây nói về chuyển động thẳng biến đổi đều là không đúng?
Câu 2 :
Hãy nêu đầy đủ các tính chất đặc trưng cho chuyển động thẳng nhanh dần đều
Câu 3 :
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
Câu 4 :
Chuyển động thẳng biến đổi đều là chuyển động
Câu 5 :
Trong công thức tính quãng đường đi được của chuyển động thẳng chậm dần đều cho đến khi dừng lại: \(s = {v_0}t + \frac{1}{2}a{t^2}\) thì:
Câu 6 :
Chọn phát biểu sai?
Câu 7 :
Gia tốc là một đại lượng
Câu 8 :
Chọn câu đúng?
Câu 9 :
Chọn câu đúng nhất?
Câu 10 :
Xét một vật chuyển động trên một đường thẳng và không đổi hướng, gọi a là gia tốc, vo là vận tốc ban đầu, v là vận tốc tại thời điểm nào đó. Trong các kết luận sau, kết luận nào đúng?
Câu 11 :
Nếu chọn chiều dương là chiều chuyển động thì:
Câu 12 :
Chuyển động thẳng biến đổi đều là chuyển động có
Câu 13 :
Chọn phát biểu sai?
Câu 14 :
Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
Câu 15 :
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Câu 16 :
Chọn câu đúng? Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
Câu 17 :
Đặc điểm nào sau đây sai với chuyển động thẳng nhanh dần đều?
Câu 18 :
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
Câu 19 :
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
Câu 20 :
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai?
Câu 21 :
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
Câu 22 :
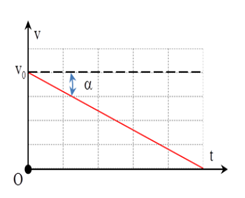
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
Câu 23 :
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
Câu 24 :
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
Câu 25 :
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
Câu 26 :
Chọn câu sai trong các câu sau đây:
Câu 27 :
Ở một nơi trên trái đất (tức ở một vĩ độ xác định) thời gian rơi tự do của một vật phụ thuộc vào:
Câu 28 :
Chọn câu sai trong các câu sau :
Câu 29 :
Chọn câu đúng trong các câu sau :
Câu 30 :
Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Phương trình của vật khi chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m, chiều dương hướng xuống là : (g = 9,8m/s2)
Câu 31 :
Câu nào sau đây nói về sự rơi là đúng?
Câu 32 :
Chuyển động của vật nào dưới đây có thể coi như chuyển động rơi tự do?
Câu 33 :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi:
Một vật rơi không vận tốc đầu từ độ cao \(80m\) xuống đất. Lấy \(g = 10m/{s^2}\) Câu 34
Tính quãng đường vật rơi trong 0,5s đầu tiên?
Câu 35
Thời gian rơi khi vật chạm đất là:
Câu 36 :
Sau \(2s\) kể từ lúc giọt nước thứ \(2\) bắt đầu rơi, khoảng cách giữa \(2\) giọt nước là \(25m\). Tính xem giọt nước thứ \(2\) được nhỏ rơi trễ hơn giọt nước thứ nhất bao lâu ? Lấy \(g = 10m/{s^2}\)
Câu 37 :
Ở một tầng tháp cách mặt đất \(45m\), một người thả rơi một vật. Một giây sau người đó ném vật thứ 2 xuống theo hướng thẳng đứng. Hai vật chạm đất cùng lúc. Tính vận tốc ném của vật thứ 2. Lấy \(g = 10m/{s^2}\)
Câu 38 :
Từ độ cao 20m, phải ném một vật thẳng đứng với vận tốc v0 bằng bao nhiêu để vật này tới mặt đất sớm hơn 1s so với vật rơi tự do
Câu 39 :
Một vật rơi tự do từ độ cao 19,6m xuống đất. Vận tốc khi chạm đất của vật là bao nhiêu ? Lấy \(g{\rm{ }} = {\rm{ }}9,8m/{s^2}\)
Một vật rơi từ độ cao \(45m\) xuống đất. Lấy \(g = 10m/{s^2}\) Câu 40
Tính quãng đường vật rơi trong $2s$ cuối cùng ?
Câu 41
Tính quãng đường vật rơi sau $2s$?
Câu 42 :
Một vật rơi tự do tại nơi có \(g = 10m/{s^2}\). Trong \(2\) giây cuối vật rơi được \(180m\). Tính thời gian rơi và độ cao buông vật?
Câu 43 :
Một vật được buông rơi tự do tại nơi có \(g = 10{\rm{ }}m/{s^2}\). Quãng đường vật đi được trong giây thứ 3 có giá trị là:
Câu 44 :
Thả rơi một vật từ độ cao \(74,8m\). Thời gian để vật đi hết 20m đầu tiên và 20m cuối cùng? Lấy \(g=9,8m/s^2\)
Câu 45 :
Hai viên bi A và B được thả rơi tự do từ cùng độ cao. Bi A rơi sau bi B \(0,5s\). Tính khoảng cách giữa \(2\) bi sau \(2s\) kể từ lúc bi B bắt đầu rơi? Lấy \(g = 10m/{s^2}\).
Câu 46 :
Hai giọt nước rơi cách nhau 1s. Tìm khoảng cách giữa hai giọt sau khi giọt thứ 2 rơi được 1s? Lấy \(g = 10m/{s^2}\).
Câu 47 :
Một vật rơi tự do từ độ cao 80m. Lấy g = 10m/s2. Quãng đường vật rơi được trong 2s và trong giây thứ 2 là:
Câu 48 :
Một vật rơi tự do từ độ cao h so với mặt đất, cho gia tốc rơi tự do g = 10 m/s2. Biết trong 1 s cuối cùng vật rơi được quãng đường bằng với quãng đường rơi được trong \(\sqrt 3 s\) đầu tiên. Giá trị của h bằng
Câu 49 :
Một vật được thả rơi tự do, khi chạm đất tốc độ của vật là 30 m/s. Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống, lấy g = 10m/s2. Khi tốc độ của vật là 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s).
Câu 50 :
Một vật rơi tự do không vận tốc đầu từ một điểm M cách mặt đất 50m. Lấy g = 10m/s2. Viết phương trình chuyển động của vật khi chọn gốc toạ độ ở mặt đất và chiều dương hướng xuống?
Câu 51 :
Từ một đỉnh tháp người ta thả rơi tự do vật thứ nhất. Hai giây sau, ở tầng tháp thấp hơn 40 m, người ta thả rơi tự do vật thứ hai. Lấy g = 10m/s2. Sau bao lâu hai vật sẽ chạm nhau tính từ lúc vật thứ nhất được thả rơi?
Câu 52 :
a) Nêu các đặc điểm của sự rơi tự do. b) Một giọt nước rơi tự do từ độ cao \(45m\) xuống đất. Cho \(g = 10m/{s^2}\). Thời gian giọt nước rơi tới mặt đất là bao nhiêu?
Câu 53 :
Một vật được ném ngang từ độ cao $h$ so với mặt đất ở nơi có gia tốc rơi tự do $g$. Thời gian chạm đất của vật là:
Câu 54 :
Ở nơi có gia tốc rơi tự gio là $g$, từ độ cao $h$ so với mặt đất, một vật được ném ngang với tốc độ ban đầu $v$. Tầm bay của vật là:
Câu 55 :
Quỹ đạo của chuyển động ném ngang là:
Câu 56 :
Viên bi A khối lượng gấp đôi viên bi B. Cùng lúc, từ mái nhà, bi A được thả rơi không vận tốc đầu, bi B được ném theo phương ngang. Bỏ qua sức cản của không khí. Kết luận nào sau đây đúng?
Câu 57 :
Một vật được ném ngang ở độ cao h so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Sau \(5s\) vật chạm đất. Độ cao h bằng:
Câu 58 :
Một vật được ném ngang ở độ cao \(45{\rm{ }}m\) so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Thời gian vật rơi tới khi chạm đất là:
Câu 59 :
Một viên bi được ném theo phương ngang với vận tốc \(2{\rm{ }}m/s\) từ độ cao \(5{\rm{ }}m\) so với mặt đất. Lấy \(g = 10{\rm{ }}m/{s^2}\). Tầm ném xa của viên bi là:
Câu 60 :
Để tăng tầm xa của vật ném ngang theo phương ngang với sức cản không khí không đáng kể thì biện pháp nào sau đây có hiệu quả nhất?
Câu 61 :
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao h so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều vận tốc đầu, Oy hướng thẳng đứng xuống dưới. Gốc thời gian là lúc ném. Lấy \(g = 10m/{s^2}\). Phương trình quỹ đạo của vật là:
Câu 62 :
Một vật được ném theo phương ngang với vận tốc \({v_0}\) từ độ cao \(h\) so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo phương vận tốc ban đầu, Oy hướng thẳng đứng xuống dưới, gốc thời gian từ lúc ném. Độ lớn vận tốc của vật tại thời điểm t xác định bằng biểu thức:
Câu 63 :
Một viên bi lăn theo cạnh của một mặt bàn nằm ngang cao \(1,25{\rm{ }}m\). Khi ra khỏi mép bàn nó rơi xuống nền nhà, cách mép bàn theo phương ngang \(2{\rm{ }}m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tốc độ của viên bi khi nó ở mép bàn là:
Câu 64 :
Một máy bay trực thăng cứu trợ bay với vận tốc không đổi \({v_0}\) theo phương ngang ở độ cao \(1500{\rm{ }}m\) so với mặt đất. Máy bay chỉ có thể tiếp cận được khu vực cách điểm cứu trợ \(2{\rm{ }}km\) theo phương ngang. Lấy \(g = 9,8{\rm{ }}m/{s^2}\). Để hàng cứu trợ thả từ máy bay tới được điểm cần cứu trợ thì máy bay phải bay với vận tốc bằng:
Câu 65 :
Một vật được ném ngang từ độ cao \(45{\rm{ }}m\) so với mặt đất ở nơi cố gia tốc rơi tự do \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \(40{\rm{ }}m/s\). Tốc độ của vật khi chạm đất là:
Câu 66 :
Một vật được ném ngang từ độ cao \(h\) ở nơi có gia tốc rơi tự do là \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \({v_0}\). Biết sau \(2s\), véctơ vận tốc của vật hợp với phương ngang góc \({30^0}\). Tốc độ ban đầu của vật gần nhất giá trị nào sau đây?
Câu 67 :
Từ vị trí A, một vật được ném ngang với tốc độ \({v_0} = 2m/s\). Sau đó 1s, tại vị trí B có cùng độ cao với A người ta ném thẳng đứng một vật xuống dưới với tốc độ ban đầu \({v_0}'\). Biết \(AB = 6m\) và hai vật gặp nhau trong quá trình chuyển động. Lấy \(g = 10m/{s^2}\). Vận tốc \({v_0}'\) gần nhất với giá trị nào sau đây?
Câu 68 :
Ném vật theo phương ngang với vận tốc 10 m/s từ độ cao 40 m xuống đất. Lấy g = 10 m/s2. Phương trình quỹ đạo của vật và toạ độ của vật sau 2s là:
Câu 69 :
Bi A có khối lượng gấp đôi bi B. Cùng một lúc tại tầng 3 trường THPT Trần Quốc Tuấn, bi A được thả rơi tự do, bi B được ném theo phương ngang (bỏ qua mọi lực cản) thì:
Câu 70 :
Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao 180cm. Khi ra khỏi mép, nó rơi xuống nền nhà tại điểm cách mép bàn 90cm (theo phương ngang). Lấy \(g = 10m/{s^2}\). Tính vận tốc của bi lúc rời khỏi bàn và viết phương trình quỹ đạo của viên bi.
Câu 71 :
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao \(h\) so với mặt đất. Chọn hệ trục toạ độ \(Oxy\) sao cho gốc O trùng với vị trí ném, Ox theo chiều \(\overrightarrow {{v_0}} \), Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc bắt đầu ném. Phương trình quỹ đạo của vật là: (với \(g = 10m/{s^2}\) )
Câu 72 :
Chuyển động ném ngang là gì?
Câu 73 :
Chuyển động nào sau đây là chuyển động ném ngang?
Câu 74 :
Trong chuyển động ném ngang, thành phần chuyển động theo phương thẳng đứng là chuyển động gì?
Câu 75 :
Trong chuyển động ném ngang, thành phần chuyển động theo phương nằm ngang là chuyển động gì?
Câu 76 :
Tầm xa không phụ thuộc vào đại lượng nào?
Câu 77 :
Nếu ném từ độ cao khác nhau ném ngang các vật với cùng vận tốc thì:
Lời giải và đáp án
Câu 1 :
Câu nào dưới đây nói về chuyển động thẳng biến đổi đều là không đúng?
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C- sai vì: + Khi vật chuyển động nhanh dần đều thì: Véctơ gia tốc và véctơ vận tốc luôn cùng hướng + Khi vật chuyển động chậm dần đều thì: Véctơ gia tốc và véctơ vận tốc luôn ngược hướng
Câu 2 :
Hãy nêu đầy đủ các tính chất đặc trưng cho chuyển động thẳng nhanh dần đều
Đáp án : D Lời giải chi tiết :
Các đặc trưng của chuyển động thẳng nhanh dần đều gồm cả A, B và C
Câu 3 :
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
Đáp án : C Lời giải chi tiết :
Chất điểm chuyển động nhanh dần đều nếu a và v cùng dấu (a.v > 0) => Phương án C - sai vì: a.v0 < 0
Câu 4 :
Chuyển động thẳng biến đổi đều là chuyển động
Đáp án : C Lời giải chi tiết :
Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi - Ta để ý rằng khái niệm vectơ vận tốc không đổi nghĩa là trong suốt quá trình chuyển động cả độ lớn và phương chiều của vận tốc là không thay đổi điều này không phù hợp với chuyển động thẳng biến đổi đều có độ lớn vận tốc là một hàm bậc nhất của thời gian
Câu 5 :
Trong công thức tính quãng đường đi được của chuyển động thẳng chậm dần đều cho đến khi dừng lại: \(s = {v_0}t + \frac{1}{2}a{t^2}\) thì:
Đáp án : B Lời giải chi tiết :
Trong chuyển động thẳng chậm dần đều thì vận tốc và gia tốc ngược dấu nhau, quãng đường là đại lượng không âm
Câu 6 :
Chọn phát biểu sai?
Đáp án : C Lời giải chi tiết :
Trong chuyển động thẳng biến đổi đều thì
Câu 7 :
Gia tốc là một đại lượng
Đáp án : D Lời giải chi tiết :
Gia tốc là đại lượng vecto đặc trưng cho sự biến đổi nhanh hay chậm của vận tốc
Câu 8 :
Chọn câu đúng?
Đáp án : D Lời giải chi tiết :
Trong chuyển động nhanh dần đều tích của vận tốc và gia tốc luôn dương.
Câu 9 :
Chọn câu đúng nhất?
Đáp án : D Lời giải chi tiết :
Gia tốc của chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.
Câu 10 :
Xét một vật chuyển động trên một đường thẳng và không đổi hướng, gọi a là gia tốc, vo là vận tốc ban đầu, v là vận tốc tại thời điểm nào đó. Trong các kết luận sau, kết luận nào đúng?
Đáp án : D Lời giải chi tiết :
Trong chuyển động thẳng nhanh dần đều thì a và v luôn cùng dấu
Câu 11 :
Nếu chọn chiều dương là chiều chuyển động thì:
Đáp án : D Lời giải chi tiết :
Nếu chọn chiều dương là chiều chuyển động thì: + Véctơ gia tốc của chuyển động thẳng nhanh dần đều hướng theo chiều dương + Véctơ gia tốc của chuyển động thẳng chậm dần đều hướng ngược chiều dương + Véctơ vận tốc của chuyển động thẳng chậm dần đều và nhanh dần đều đều hướng theo chiều dương
Câu 12 :
Chuyển động thẳng biến đổi đều là chuyển động có
Đáp án : D Lời giải chi tiết :
Chuyển động thẳng biến đổi đều là chuyển động có gia tốc không đổi theo thời gian
Câu 13 :
Chọn phát biểu sai?
Đáp án : D Lời giải chi tiết :
Trong chuyển động chậm dần đều thì vectơ gia tốc và vận tốc ngược chiều nhau
Câu 14 :
Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
Đáp án : D Phương pháp giải :
Sử dụng lí thuyêt về gia tốc Lời giải chi tiết :
Cả A, B, C đều đúng
Câu 15 :
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Đáp án : A Lời giải chi tiết :
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Câu 16 :
Chọn câu đúng? Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
Đáp án : D Phương pháp giải :
Đọc phương trình vận tốc theo thời gian của vật Lời giải chi tiết :
A - sai vì chuyển động thẳng đều có vận tốc không đổi B - sai vì: \(a = 3,{v_0} = 0\) => vật chuyển động nhanh dần C - sai vì \(a = - 2;{v_0} = 9\) => vật chuyển động chậm dần D- đúng
Câu 17 :
Đặc điểm nào sau đây sai với chuyển động thẳng nhanh dần đều?
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Vận tốc của vật âm hay dương phụ thuộc vào chiều chuyển động của vật so với chiều dương của trục tọa độ mà ta chọn.
Câu 18 :
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức phương trình vận tốc: \(v = {v_0} + at\) Lời giải chi tiết :
Ta có: Vận tốc được xác định bằng biểu thức \(v = {v_0} + at\) A, B, D - đúng C -sai vì: \(v = {v_0} + at \to v = 2 + 4.2 = 10m/s\left( {{v_0} = 2,t = 2} \right)\)
Câu 19 :
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Đọc phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\) Lời giải chi tiết :
Từ phương trình chuyển động ta có: \(\left\{ \begin{array}{l}{x_0} = 100m\\{v_0} = 10m/s\\a = 4m/{s^2}\end{array} \right.\) => Vật chuyển động nhanh dần đều với gia tốc \(a = 4{\rm{ }}m/{s^2}\) Tọa độ lúc ban đầu của vật là \({x_0} = 100m\) Vận tốc của vật tại thời điểm ban đầu: \({v_0} = 10m/s\)
Câu 20 :
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai?
Đáp án : A Phương pháp giải :
Đọc phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\) Lời giải chi tiết :
Ta có: Gia tốc của vật là: a = 8m/s2 => A - sai
Câu 21 :
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
Đáp án : C Lời giải chi tiết :
Ta có phương trình tọa độ theo thời gian của chất điểm trong chuyển đông thẳng biến đổi đều có dạng: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\) => Đồ thị của tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều là một nhánh parabol (dạng đồ thị giống hàm \(y = ax^2+bx+c\) nhưng ở đây ta có t>0 lên đồ thị chỉ là một nhánh parabol)
Câu 22 :
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
Đáp án : A Lời giải chi tiết :
Đồ thị v - t trong đó a > 0 là đồ thị A
Câu 23 :
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
Đáp án : A Lời giải chi tiết :
Đồ thị a - t của chất điểm chuyển động thẳng biến đổi đều có dạng là đường thẳng song song với trục Ot
Câu 24 :
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
Đáp án : C Phương pháp giải :
Vận dụng biểu thức xác định gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\) Lời giải chi tiết :
Ta có: \(36km/h = 10m/s\) + Gia tốc của chuyển động: \(a = \frac{{10 - 0}}{{20}} = 0,5m/{s^2}\) + Phương trình vận tốc của vật: \(v = at = 0,5t\) Thời gian để tàu đạt vận tốc \(54{\rm{ }}km/h = 15m/s\) tính từ lúc tàu đạt tốc độ 36km/h là: \(\Delta t = \frac{{15}}{{0,5}} - 20 = 30 - 20 = 10{\rm{s}}\)
Câu 25 :
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
Đáp án : A Phương pháp giải :
+ Xác định xem trong khoảng thời gian \(\Delta t\) vật có đổi chiều không + Thay t vào phương trình chuyển động để xác định quãng đường Lời giải chi tiết :
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v = 4 - 2t \to v = 0 \leftrightarrow t = 2{\rm{s}}\) , vật sẽ đổi chiều chuyển động sau $2s$. 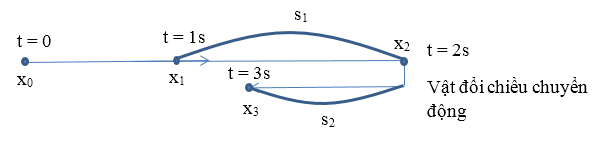 Do vậy quãng đường đi được của vật được tính: \(s = {s_1} + {s_2} = \left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_2}} \right| = \left| {4 - 3} \right| + \left| {3 - 4} \right| = 2m\)
Câu 26 :
Chọn câu sai trong các câu sau đây:
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Trong chân không, mọi vật đều rơi nhanh như nhau.
Câu 27 :
Ở một nơi trên trái đất (tức ở một vĩ độ xác định) thời gian rơi tự do của một vật phụ thuộc vào:
Đáp án : C Lời giải chi tiết :
Ở một nơi trên trái đất (tức ở một vĩ độ xác định) => cùng g => Thời gian rơi tự do của một vật phụ thuộc vào độ cao của vật
Câu 28 :
Chọn câu sai trong các câu sau :
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì ở những nơi khác nhau - gia tốc rơi tự do sẽ khác nhau.
Câu 29 :
Chọn câu đúng trong các câu sau :
Đáp án : C Lời giải chi tiết :
A - sai vật nào có lực cản nhỏ hơn sẽ rơi nhanh hơn B - sai vì trong chân không, các vật rơi như nhau C - đúng D - sai vì ở cùng một nơi trên Trái Đất, các vật đều rơi tự do với cùng một gia tốc
Câu 30 :
Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Phương trình của vật khi chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m, chiều dương hướng xuống là : (g = 9,8m/s2)
Đáp án : C Phương pháp giải :
Sử dụng phương trình chuyển động của vật rơi tự do: \(y = {y_0} + {v_0}t + \frac{1}{2}g{t^2}\) + Xác định vận tốc ban đầu \({v_0}\) + Xác định vị trí ban đầu của vật so với gốc tọa độ Lời giải chi tiết :
Ta có: + Vật rơi không vận tốc đầu: \( \to {v_0} = 0\) Gốc tọa độ tại O ở phía dưới A một đoạn 196m, chiều dương hướng xuống + Tọa độ ban đầu của vật: \({y_0} = - 196m\) => Phương trình chuyển động của vật: \(y = - 196 + \frac{1}{2}.9,8{t^2} = 4,9{t^2} - 196\left( m \right)\)
Câu 31 :
Câu nào sau đây nói về sự rơi là đúng?
Đáp án : B Lời giải chi tiết :
A - sai vì: Khi không có lực cản các vật đều rơi như nhau B - đúng C - sai vì: Các vật rơi với cùng gia tốc \(g\) như nhau tại cùng 1 nơi D - sai vì: Vận tốc của vật chạm đất phụ thuộc vào độ cao của vật khi rơi
Câu 32 :
Chuyển động của vật nào dưới đây có thể coi như chuyển động rơi tự do?
Đáp án : B Phương pháp giải :
Vận dụng định nghĩa về sự rơi tự do Sự rơi tự do (chuyển động rơi tự do) là sự rơi của các vật chỉ chịu tác dụng của trọng lực. Lời giải chi tiết :
Ta có: Sự rơi tự do (chuyển động rơi tự do) là sự rơi của các vật chỉ chịu tác dụng của trọng lực. => Chuyển động của một viên gạch rơi từ độ cao 3m xuống đất là chuyển động rơi tự do.
Câu 33 :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi:
Đáp án : C Lời giải chi tiết :
Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi tự do hay nói cách khác là chuyển động thẳng nhanh dần đều Một vật rơi không vận tốc đầu từ độ cao \(80m\) xuống đất. Lấy \(g = 10m/{s^2}\) Câu 34
Tính quãng đường vật rơi trong 0,5s đầu tiên?
Đáp án : C Phương pháp giải :
Thay t vào biểu thức: \(y = {y_0} + \frac{1}{2}g{t^2}\) Lời giải chi tiết :
Ta có, quãng đường vật rơi được trong 0,5s đầu tiên là: \(s = y = \frac{1}{2}g{t^2} = 5.{\left( {0,5} \right)^2} = 1,25m\) Câu 35
Thời gian rơi khi vật chạm đất là:
Đáp án : A Phương pháp giải :
Áp dụng biểu thức : \(y = {y_0} + \frac{1}{2}g{t^2}\) Lời giải chi tiết :
Chọn gốc tọa độ tại vị trí ban đầu của vật, ta có: Thời gian rơi của vật: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.80}}{{10}}} = 4{\rm{s}}\)
Câu 36 :
Sau \(2s\) kể từ lúc giọt nước thứ \(2\) bắt đầu rơi, khoảng cách giữa \(2\) giọt nước là \(25m\). Tính xem giọt nước thứ \(2\) được nhỏ rơi trễ hơn giọt nước thứ nhất bao lâu ? Lấy \(g = 10m/{s^2}\)
Đáp án : B Phương pháp giải :
+ Chọn hệ quy chiếu: gốc tọa độ, chiều chuyển động + Chọn gốc thời gian + Viết phương trình chuyển động của 2 giọt nước + Giải phương trình : \({s_1} - {s_2} = \Delta s\) Lời giải chi tiết :
+ Chọn HQC : - Gốc tọa độ O tại vị trí rơi. - Chiều dương hướng xuống + Gốc thời gian \(t = 0\) là lúc giọt \(2\) rơi \( \to \left\{ \begin{array}{l}{t_{{0_1}}} \ne 0\\{t_{{0_2}}} = 0\end{array} \right.\) + Phương trình chuyển động của \(2\) giọt nước là : \({s_1} = \frac{1}{2}g{\left( {t + {t_{01}}} \right)^2}\) và \({s_2} = \frac{1}{2}g{t^2}\) + Theo đề bài tại \(t = 2s\) ta có : \({s_1} - {s_2} = 25m\) \(\begin{array}{l} \leftrightarrow \frac{1}{2}g{\left( {t + {t_{01}}} \right)^2} - \frac{1}{2}g{t^2} = 25\\ \leftrightarrow 5{\left( {2 + {t_{01}}} \right)^2} - {5.2^2} = 25\\ \leftrightarrow t_{01}^2 + 4{t_{01}} - 5 = 0\\ \to \left[ \begin{array}{l}{t_{01}} = 1\\{t_{01}} = - 5(loai)\end{array} \right.\end{array}\) \( \to {t_{01}} = 1s\) Vậy giọt thứ 2 rơi sau giọt thứ nhất 1s.
Câu 37 :
Ở một tầng tháp cách mặt đất \(45m\), một người thả rơi một vật. Một giây sau người đó ném vật thứ 2 xuống theo hướng thẳng đứng. Hai vật chạm đất cùng lúc. Tính vận tốc ném của vật thứ 2. Lấy \(g = 10m/{s^2}\)
Đáp án : D Phương pháp giải :
+ Chọn hệ quy chiếu: Vị trí ban đầu, chiều dương + Chọn gốc thời gian + Viết phương trình chuyển động của mỗi vật: \(s = \frac{1}{2}g{t^2}\) Lời giải chi tiết :
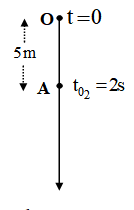 + Chọn HQC : - O tại vị trí thả vật, chiều dương hướng xuống + Gốc thời gian \(t = 0\): lúc thả vật 1 \( \to \left\{ \begin{array}{l}{t_{{0_1}}} = 0\\{t_{{0_2}}} = 1s\end{array} \right.\) + Lập các phương trình chuyển động : - PT của vật 1: \({s_1} = \frac{1}{2}g{t^2} = 5{t^2}\) (1) - PT của vật 2: \({s_2} = {v_0}\left( {t - 1} \right) + \frac{1}{2}g{\left( {t - 1} \right)^2} = {v_0}\left( {t - 1} \right) + 5{\left( {t - 1} \right)^2}\) (2) Ta có: + Thời gian vật 1 chuyển chạm đất là: \({s_1} = 5{t^2} = 45 \to t = \sqrt {\frac{{45}}{5}} = 3{\rm{s}}\) + Mặt khác, vật 1 và vật 2 chạm đất cùng lúc, thay \(t = 3{\rm{s}}\) vào phương trình (2), ta được: \(\begin{array}{l}{v_0}\left( {3 - 1} \right) + 5{\left( {3 - 1} \right)^2} = 45\\ \leftrightarrow 2{v_0} + 20 = 45\\ \to {v_0} = 12,5m/s\end{array}\)
Câu 38 :
Từ độ cao 20m, phải ném một vật thẳng đứng với vận tốc v0 bằng bao nhiêu để vật này tới mặt đất sớm hơn 1s so với vật rơi tự do
Đáp án : A Phương pháp giải :
+ Viết phương trình chuyển động của mỗi vật - Khi bị ném - Khi rơi tự do + Vận dụng biểu thức: \({\rm{s}} = {v_0}t + \frac{1}{2}g{t^2}\) Lời giải chi tiết :
Các phương trình chuyển động: + PT chuyển động rơi tự do: \({s_1} = \frac{1}{2}g{t^2} = 5{t^2}\) (1) + PT chuyển động khi vật bị ném: \({s_2} = {v_0}t' + \frac{1}{2}gt{'^2} = {v_0}t + 5t{'^2}\) (2) Ta có, thời gian vật rơi tự do chạm đất:\({s_1} = 5{t^2} = 20 \to t = 2{\rm{s}}\) Theo đề : \(t - t' = 1 \to t' = 1{\rm{s}}\) Thay vào (2) ta được : \(20 = 5 + {v_0} \to {v_0} = 15m/s\)
Câu 39 :
Một vật rơi tự do từ độ cao 19,6m xuống đất. Vận tốc khi chạm đất của vật là bao nhiêu ? Lấy \(g{\rm{ }} = {\rm{ }}9,8m/{s^2}\)
Đáp án : B Phương pháp giải :
+ Vận dụng phương trình chuyển động của vật rơi tự do: \(s = \dfrac{1}{2}g{t^2}\) + Vận dụng phương trình vận tốc của vật rơi tự do: \(v = gt\) Lời giải chi tiết :
+ Phương trình của chuyển động rơi tự do: \(s = \dfrac{{g{t^2}}}{2} = 9,8.\dfrac{{{t^2}}}{2} = 4,9{t^2}\) + Phương trình vận tốc của vật: \(v = {v_o} + gt = 9,8t\) + Khi vật chạm đất: \(s = 9,8.\dfrac{{{t^2}}}{2} = 19,6 \Rightarrow t = 2\left( s \right)\) Vận tốc của vật khi chạm đất là: \(v = gt = 9,8t = 9,8.2 = 19,6m/s\) Một vật rơi từ độ cao \(45m\) xuống đất. Lấy \(g = 10m/{s^2}\) Câu 40
Tính quãng đường vật rơi trong $2s$ cuối cùng ?
Đáp án : B Phương pháp giải :
+ Tính thời gian vật vật chạm đất : \(t = \sqrt {\dfrac{{2h}}{g}} \) + Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\) + Xác định quãng đường vật đi được trong n(s) cuối : \(\Delta S = {S_t} - {S_{t - n}}\) Lời giải chi tiết :
+ Thời gian vật đi hết quãng đường \(45m\) là: \(S = \dfrac{{g{t^2}}}{2} = 45 \Rightarrow {t^2} = \dfrac{{45.2}}{{10}} \Rightarrow t = 3\left( s \right)\) Quãng đường vật đi được trong \(1s\) đầu là: \({s_1} = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}{10.1^2} = 5m\) + Trong \(2\left( s \right)\) cuối cùng quãng đường vật đi được là:\(\Delta S = 45 - {s_1} = 45 - 5 = 40m\) Câu 41
Tính quãng đường vật rơi sau $2s$?
Đáp án : D Phương pháp giải :
Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \frac{1}{2}g{t^2}\) Lời giải chi tiết :
Ta có: Phương trình chuyển động của vật rơi tự do là \(s = \dfrac{{g{t^2}}}{2}\) => Sau \(2\left( s \right)\) quãng đường vật đi được là: \(s = \dfrac{{g{t^2}}}{2} = 10.\dfrac{{{2^2}}}{2} = 20\left( m \right)\)
Câu 42 :
Một vật rơi tự do tại nơi có \(g = 10m/{s^2}\). Trong \(2\) giây cuối vật rơi được \(180m\). Tính thời gian rơi và độ cao buông vật?
Đáp án : A Phương pháp giải :
Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\) Lời giải chi tiết :
+ Trong \(2\left( s \right)\) cuối cùng quãng đường vật đi được là \(180{\rm{ }}m\) ta có: \(\begin{array}{l}\Delta S = {S_t} - {S_{t - 2}} \\= 180 = \dfrac{{g{t^2}}}{2} - \dfrac{{g.{{\left( {t - 2} \right)}^2}}}{2} \\\Rightarrow {t^2} - {\left( {t - 2} \right)^2} = 36\\ \Rightarrow 4t -4 = 36 \Rightarrow t = 10\left( s \right)\end{array}\) + Độ cao buông vật là: \(s = \dfrac{{g{t^2}}}{2}\) $= 500 m$
Câu 43 :
Một vật được buông rơi tự do tại nơi có \(g = 10{\rm{ }}m/{s^2}\). Quãng đường vật đi được trong giây thứ 3 có giá trị là:
Đáp án : C Phương pháp giải :
+ Vận dụng phương trình chuyển động của vật rơi tự do : \(S = \frac{1}{2}g{t^2}\) + Quãng đường vật đi được trong giây thứ n : \(\Delta S = {S_n} - {S_{n - 1}}\) Lời giải chi tiết :
+ Phương trình chuyển động của vật rơi tự do là : \(S = \frac{{g{t^2}}}{2}\) + Quãng đường vật đi được trong giây thứ 3 là: \(\Delta S = {S_3} - {S_2} = \frac{{{{10.3}^2}}}{2} - \frac{{{{10.2}^2}}}{2} = 25m\)
Câu 44 :
Thả rơi một vật từ độ cao \(74,8m\). Thời gian để vật đi hết 20m đầu tiên và 20m cuối cùng? Lấy \(g=9,8m/s^2\)
Đáp án : B Phương pháp giải :
+ Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\) + Tính thời gian vật rơi hết quãng đường : \(t = \sqrt {\dfrac{{2{\rm{s}}}}{g}} \) Lời giải chi tiết :
Phương trình chuyển động của vật rơi tự do là: \(s = \dfrac{{g{t^2}}}{2}\) + Thời gian vật đi hết quãng đường \(74,8m\) là: \(s = \dfrac{{g{t^2}}}{2} \Rightarrow 74,8 = 9,8.\dfrac{{{t^2}}}{2} \\\Rightarrow t = 3,91\left( s \right)\) + Thời gian để vật đi hết 20m đầu là: \(s = \dfrac{{g{t^2}}}{2} = 20 \Rightarrow {t^2} = \dfrac{{20.2}}{{9,8}} \\\Rightarrow t = 2,02\left( s \right)\) + Công thức tính quãng đường vật đi trong \(20m\) cuối là: \(74,8 - \dfrac{{{gt^2}}}{2} = 20 \\\Rightarrow \dfrac{{g{t^2}}}{2} = 54,8 \\\Rightarrow t = 3,34\left( s \right)\) Thời gian để vật đi hết \(20m\) cuối là \(3,91{\rm{ }}-{\rm{ }}3,34{\rm{ }} = {\rm{ }}0,57{\rm{ }}\left( s \right)\)
Câu 45 :
Hai viên bi A và B được thả rơi tự do từ cùng độ cao. Bi A rơi sau bi B \(0,5s\). Tính khoảng cách giữa \(2\) bi sau \(2s\) kể từ lúc bi B bắt đầu rơi? Lấy \(g = 10m/{s^2}\).
Đáp án : A Phương pháp giải :
Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\) Lời giải chi tiết :
+ Sau \(2{\rm{ }}\left( s \right)\) viên bi B đi được quãng đường là: \({s_{{B_{}}}} = g\dfrac{{{t^2}}}{2} = 10.\dfrac{{{2^2}}}{2} = 20\left( m \right)\) Vì viên bi A rơi sau viên bi B \(0,5s\) nên quãng đường viên bi A đi được sau \(2s\) là: \({s_{{A_{}}}} = g\dfrac{{{t^2}}}{2} = 10.\dfrac{{1,{5^2}}}{2} = 11,25\left( m \right)\) + Sau \(2s\) khoảng cách giữa hai viên bi là: \(\Delta s = {s_B} - {s_A} = 20 - 11,25 = 8,75\left( m \right)\)
Câu 46 :
Hai giọt nước rơi cách nhau 1s. Tìm khoảng cách giữa hai giọt sau khi giọt thứ 2 rơi được 1s? Lấy \(g = 10m/{s^2}\).
Đáp án : C Phương pháp giải :
Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \frac{1}{2}g{t^2}\) Lời giải chi tiết :
Giả sử giọt thứ nhất rơi trước giọt thứ 2, khi đó ta có sau khi giọt thứ 2 rơi được 1s thì giọt thứ nhất rơi được 2s Vậy khoảng cách giữa chúng khi giọt thứ 2 rơi được 1s là: \(\Delta s = {s_1} - {s_2} = \frac{{g{t_1}^2}}{2} - \frac{{g.{t_2}^2}}{2} = 10.\frac{{{2^2}}}{2} - 10.\frac{{{1^2}}}{2} = 15\left( m \right)\)
Câu 47 :
Một vật rơi tự do từ độ cao 80m. Lấy g = 10m/s2. Quãng đường vật rơi được trong 2s và trong giây thứ 2 là:
Đáp án : B Phương pháp giải :
Quãng đường vật rơi trong n giây : \({s_{t = n}} = \dfrac{1}{2}g.{n^2}\) Quãng đường vật rơi trong giây thứ n: \({s_n} = {s_{t = n}} - {s_{t = n - 1}} = \dfrac{1}{2}g.{n^2} - \dfrac{1}{2}g.{\left( {n - 1} \right)^2}\) Lời giải chi tiết :
Ta có : \(\left\{ \begin{array}{l}h = 80m\\g = 10m/{s^2}\end{array} \right.\) Quãng đường vật rơi trong 2s là : \({s_{t = 2}} = \dfrac{1}{2}g.{t^2} = \dfrac{1}{2}{.10.2^2} = 20m\) Quãng đường vật rơi trong giây thứ hai là: \({s_2} = {s_{t = 2}} - {s_{t = 1}} = \dfrac{1}{2}{.10.2^2} - \dfrac{1}{2}{.10.1^2} = 15m\)
Câu 48 :
Một vật rơi tự do từ độ cao h so với mặt đất, cho gia tốc rơi tự do g = 10 m/s2. Biết trong 1 s cuối cùng vật rơi được quãng đường bằng với quãng đường rơi được trong \(\sqrt 3 s\) đầu tiên. Giá trị của h bằng
Đáp án : D Phương pháp giải :
Áp dụng công thức tính quãng đường đi được của vật rơi tự do trong thời gian t giây: \(s = \frac{1}{2}.g.{t^2}\) Trong giây cuối cùng quãng đường vật đi được là \({S_c} = h - \frac{1}{2}.g.{({t_h} - 1)^2}\) với thlà thời gian vật rơi chạm đất: \({t_h} = \sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Quãng đường đi được của vật rơi tự do trong thời gian \(\sqrt{3}s\)đầu tiên \(s=\frac{1}{2}.g.{{t}^{2}}=\frac{1}{2}.g.3=1,5g\) Trong giây cuối cùng quãng đường vật đi được là \({{S}_{c}}=h-\frac{1}{2}.g.{{({{t}_{h}}-1)}^{2}}\) với \({{t}_{h}}\) là thời gian vật rơi chạm đất: \({{t}_{h}}=\sqrt{\frac{2h}{g}}\text{ }\) Vậy ta có: \({{S}_{c}}=h-\frac{1}{2}.g.{{\left( \sqrt{\frac{2h}{g}}-1 \right)}^{2}}=\sqrt{2gh}-\frac{1}{2}g\) Mà \(s={{S}_{c}}\) nên ta có: \(\sqrt{2gh}-0,5g=1,5g\Leftrightarrow \sqrt{2gh}=2g\Leftrightarrow h=2g=20m\)
Câu 49 :
Một vật được thả rơi tự do, khi chạm đất tốc độ của vật là 30 m/s. Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống, lấy g = 10m/s2. Khi tốc độ của vật là 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s).
Đáp án : B Phương pháp giải :
Áp dụng công thức: - Thời gian từ lúc rơi đến khi chạm đất: v = g.t - Độ cao lúc thả vật:\(h = \frac{{g.{t^2}}}{2}\) - Công thức độc lập với thời gian: \(v_{^1}^2 - v_0^2 = 2g{h_1}\) - Công thức vận tốc v = gt Lời giải chi tiết :
Tóm tắt: Tốc độc của vật khi chạm đất: \({{v}_{cd}}~=30m/s\) Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống, g = 10m/s2. Khi v = 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s). Giải: + Thời gian từ lúc rơi đến khi chạm đất: \(v=g.t\Rightarrow t=3(s)\) + Độ cao lúc thả vật: \(h=\frac{g.{{t}^{2}}}{2}\Rightarrow h=45(m)\) + Khi tốc độ v1 = 20 m/s, ta có: \(v_{1}^{2}=2g{{h}_{1}}\Rightarrow {{h}_{1}}=20(m)\) → Vật cách mặt đất một đoạn: \(\Delta h=h-{{h}_{1}}=45-20=25(m)\) + Thời gian từ lúc thả đến khi vật đạt tốc độ là 20m/s là t1: \({{v}_{1}}=g.{{t}_{1}}\Rightarrow {{t}_{1}}=2(s)\Rightarrow {{t}_{2}}=t-{{t}_{1}}=1(s)\)
Câu 50 :
Một vật rơi tự do không vận tốc đầu từ một điểm M cách mặt đất 50m. Lấy g = 10m/s2. Viết phương trình chuyển động của vật khi chọn gốc toạ độ ở mặt đất và chiều dương hướng xuống?
Đáp án : B Phương pháp giải :
Phương trình chuyển động của vật có dạng tổng quát: \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\) Lời giải chi tiết :
Chọn gốc thời gian là lúc thả rơi vật. Gốc toạ độ ở mặt đất và chiều dương hướng xuống Phương trình chuyển động của vật có dạng : \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\) Ta có: \(\left\{ \begin{array}{l}{y_0} = {y_M} = - 50m\\{v_0} = 0\\{t_0} = 0\\a = g = 9,8m/{s^2}\end{array} \right. \Rightarrow y = - 50 + \frac{1}{2}.10.{t^2} \Rightarrow y = - 50 + 5{t^2}\,\,\left( m \right)\)
Câu 51 :
Từ một đỉnh tháp người ta thả rơi tự do vật thứ nhất. Hai giây sau, ở tầng tháp thấp hơn 40 m, người ta thả rơi tự do vật thứ hai. Lấy g = 10m/s2. Sau bao lâu hai vật sẽ chạm nhau tính từ lúc vật thứ nhất được thả rơi?
Đáp án : C Phương pháp giải :
Phương trình chuyển động dạng tổng quát: \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a{\left( {t - {t_0}} \right)^2}\) Hai vật gặp nhau: y1 = y2 Lời giải chi tiết :
Chọn trục toạ độ thẳng đứng, gốc toạ độ tại đỉnh tháp, chiều dương hướng xuống. Chọn gốc thời gian là lúc vật thứ nhất được thả rơi. Phương trình chuyển động của vật (1): \({y_1} = {y_{01}} + {v_{01}}\left( {t - {t_{01}}} \right) + \frac{1}{2}{a_1}{\left( {t - {t_{01}}} \right)^2}\) Có: \(\left\{ \begin{array}{l}{y_{01}} = 0\\{v_{01}} = 0\\{t_{01}} = 0\\{a_1} = g = 10m/{s^2}\end{array} \right. \Rightarrow {y_1} = 5{t^2}\,\,\,\left( m \right)\) Phương trình chuyển động của vật (2): \({y_2} = {y_{02}} + {v_{02}}\left( {t - {t_{02}}} \right) + \frac{1}{2}{a_2}{\left( {t - {t_{02}}} \right)^2}\) Có: \(\left\{ \begin{array}{l}{y_{02}} = 40m\\{v_{02}} = 0\\{t_{02}} = 2s\\{a_2} = g = 10m/{s^2}\end{array} \right. \Rightarrow {y_2} = 40 + 5{\left( {t - 2} \right)^2}\,\,\,\left( m \right)\) Hai vật chạm nhau (gặp nhau): \({y_1} = {y_2} \Leftrightarrow 5{t^2} = 40 + 5{\left( {t - 2} \right)^2} \Rightarrow t = 3s\) Sau 3s hai vật sẽ chạm nhau tính từ lúc vật thứ nhất được thả rơi
Câu 52 :
a) Nêu các đặc điểm của sự rơi tự do. b) Một giọt nước rơi tự do từ độ cao \(45m\) xuống đất. Cho \(g = 10m/{s^2}\). Thời gian giọt nước rơi tới mặt đất là bao nhiêu?
Đáp án : A Phương pháp giải :
+ Sử dụng lí thuyết “Bài 4: Sự rơi tự do” – Trang 24 – SGK Vật Lí 10. + Thời gian vật rơi tự do: \(t = \sqrt {\dfrac{{2h}}{g}} \) Lời giải chi tiết :
a) Các đặc điểm của sự rơi tự do: + Phương của chuyển động rơi tự do là phương thẳng đứng. + Chiều của chuyển động rơi tự do là chiều từ trên xuống dưới. + Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều b) Thời gian giọt nước rơi tới mặt đất là: \(t = \sqrt {\dfrac{{2h}}{g}} = \sqrt {\dfrac{{2.45}}{{10}}} = 3s\)
Câu 53 :
Một vật được ném ngang từ độ cao $h$ so với mặt đất ở nơi có gia tốc rơi tự do $g$. Thời gian chạm đất của vật là:
Đáp án : A Lời giải chi tiết :
Thời gian vật chạm đất: \(t = \sqrt {\dfrac{{2h}}{g}} \)
Câu 54 :
Ở nơi có gia tốc rơi tự gio là $g$, từ độ cao $h$ so với mặt đất, một vật được ném ngang với tốc độ ban đầu $v$. Tầm bay của vật là:
Đáp án : D Lời giải chi tiết :
Tầm xa: \(L = v\sqrt {\dfrac{{2h}}{g}} \)
Câu 55 :
Quỹ đạo của chuyển động ném ngang là:
Đáp án : C Lời giải chi tiết :
Phương trình quỹ đạo của vật ném ngang: \(y = \dfrac{g}{{2v_0^2}}{x^2}\) => quỹ đạo của chuyển động ném ngang là một đường parabol
Câu 56 :
Viên bi A khối lượng gấp đôi viên bi B. Cùng lúc, từ mái nhà, bi A được thả rơi không vận tốc đầu, bi B được ném theo phương ngang. Bỏ qua sức cản của không khí. Kết luận nào sau đây đúng?
Đáp án : A Phương pháp giải :
Xác định thời gian rơi tự do và thời gian vật ném ngang chạm đất Lời giải chi tiết :
Ta có: + Vật rơi tự do: \(h = \frac{1}{2}g{t^2} \to t = \sqrt {\frac{{2h}}{g}} \) + Thời gian vật ném ngang chạm đất: \(t = \sqrt {\frac{{2h}}{g}} \) Ta thấy hai khoảng thời gian trên bằng nhau => Hai viên bi chạm đất cùng lúc
Câu 57 :
Một vật được ném ngang ở độ cao h so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Sau \(5s\) vật chạm đất. Độ cao h bằng:
Đáp án : C Phương pháp giải :
Sử dụng công thức tính thời gian chạm đất: \(t = \sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, thời gian chạm đất của vật ném ngang: \(t = \sqrt {\frac{{2h}}{g}} \) Ta suy ra: \(h = \frac{1}{2}g{t^2} = \frac{1}{2}{.10.5^2} = 125m\)
Câu 58 :
Một vật được ném ngang ở độ cao \(45{\rm{ }}m\) so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Thời gian vật rơi tới khi chạm đất là:
Đáp án : D Phương pháp giải :
Sử dụng công thức tính thời gian chạm đất: \(t = \sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, thời gian chạm đất của vật ném ngang: \(t = \sqrt {\frac{{2h}}{g}} \) Thay số, ta được: \(t = \sqrt {\frac{{2.45}}{{10}}} = 3{\rm{s}}\)
Câu 59 :
Một viên bi được ném theo phương ngang với vận tốc \(2{\rm{ }}m/s\) từ độ cao \(5{\rm{ }}m\) so với mặt đất. Lấy \(g = 10{\rm{ }}m/{s^2}\). Tầm ném xa của viên bi là:
Đáp án : D Phương pháp giải :
Vận dụng biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, tầm xa của vật ném ngang: \(L = {v_0}\sqrt {\frac{{2h}}{g}} = 2\sqrt {\frac{{2.5}}{{10}}} = 2m\)
Câu 60 :
Để tăng tầm xa của vật ném ngang theo phương ngang với sức cản không khí không đáng kể thì biện pháp nào sau đây có hiệu quả nhất?
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, tầm xa của vật ném ngang: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) => Để tăng tầm xa của vật ném, ta có thể tăng vận tốc hoặc tăng độ cao của điểm nén Trong hai cách đó thì tăng vận tốc ném có hiệu quả hơn
Câu 61 :
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao h so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều vận tốc đầu, Oy hướng thẳng đứng xuống dưới. Gốc thời gian là lúc ném. Lấy \(g = 10m/{s^2}\). Phương trình quỹ đạo của vật là:
Đáp án : C Phương pháp giải :
sử dụng phương trình quỹ đạo của vật: \(y = \dfrac{g}{{2v_0^2}}{x^2}\) Lời giải chi tiết :
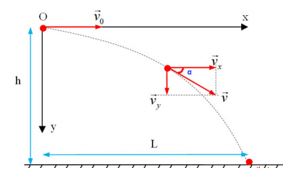 Phương trình chuyển động: + Theo phương Ox: \(x = {v_0}t\) (1) + Theo phương Oy: \(y = \dfrac{1}{2}g{t^2}\) (2) Phương trình quỹ đạo (thay t ở (1) vào (2)): \(y = \dfrac{g}{{2v_0^2}}{x^2}\) => phương trình quỹ đạo của vật ném ngang trong trường hợp trên: \(y = \dfrac{g}{{2v_0^2}}{x^2} = \dfrac{{10}}{{{{2.10}^2}}} = 0,05{{\rm{x}}^2}\) Chú ý
Phân biệt giữa phương trình quỹ đạo và phương trình chuyển động: - Phương trình quỹ đạo: \(y = \frac{g}{{2v_0^2}}{x^2}\) - Phương trình chuyển động: + Theo phương Ox: \(x = {v_0}t\) (1) + Theo phương Oy: \(y = \frac{1}{2}g{t^2}\) (2)
Câu 62 :
Một vật được ném theo phương ngang với vận tốc \({v_0}\) từ độ cao \(h\) so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo phương vận tốc ban đầu, Oy hướng thẳng đứng xuống dưới, gốc thời gian từ lúc ném. Độ lớn vận tốc của vật tại thời điểm t xác định bằng biểu thức:
Đáp án : B Lời giải chi tiết :
Ta có: + Theo phương Ox: \({v_x} = {v_0}\) + Theo phương Oy: \({v_y} = gt\) Độ lớn của vận tốc tại vị trí bất kì: \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + {g^2}{t^2}} \)
Câu 63 :
Một viên bi lăn theo cạnh của một mặt bàn nằm ngang cao \(1,25{\rm{ }}m\). Khi ra khỏi mép bàn nó rơi xuống nền nhà, cách mép bàn theo phương ngang \(2{\rm{ }}m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tốc độ của viên bi khi nó ở mép bàn là:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, tầm xa của vật: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) Vận tốc của vật khi ở mép bàn chính là vận tốc ban đầu: \( \to {v_0} = \frac{L}{{\sqrt {\frac{{2h}}{g}} }} = \frac{2}{{\sqrt {\frac{{2.1,25}}{{10}}} }} = 4m/s\)
Câu 64 :
Một máy bay trực thăng cứu trợ bay với vận tốc không đổi \({v_0}\) theo phương ngang ở độ cao \(1500{\rm{ }}m\) so với mặt đất. Máy bay chỉ có thể tiếp cận được khu vực cách điểm cứu trợ \(2{\rm{ }}km\) theo phương ngang. Lấy \(g = 9,8{\rm{ }}m/{s^2}\). Để hàng cứu trợ thả từ máy bay tới được điểm cần cứu trợ thì máy bay phải bay với vận tốc bằng:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) Lời giải chi tiết :
Ta có, tầm xa của vật: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \) \( \to {v_0} = \frac{L}{{\sqrt {\frac{{2h}}{g}} }} = \frac{2}{{\sqrt {\frac{{2.1500}}{{9,8}}} }} = 114,31m/s\)
Câu 65 :
Một vật được ném ngang từ độ cao \(45{\rm{ }}m\) so với mặt đất ở nơi cố gia tốc rơi tự do \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \(40{\rm{ }}m/s\). Tốc độ của vật khi chạm đất là:
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính thời gian chạm đất: \(t = \sqrt {\frac{{2h}}{g}} \) + Sử dụng phương trình vận tốc: - Theo phương Ox: \({v_x} = {v_0}\) - Theo phương Oy: \({v_y} = gt\) + Độ lớn của vận tốc tại vị trí bất kì: \(v = \sqrt {v_x^2 + v_y^2} \) Lời giải chi tiết :
+ Thời gian chạm đất: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.45}}{{10}}} = 3{\rm{s}}\) + Vận tốc của vật theo các phương: - Theo phương Ox: \({v_x} = {v_0} = 40\left( {m/s} \right)\) - Theo phương Oy: \({v_y} = gt = 10.3 = 30\left( {m/s} \right)\) Vận tốc của vật khi chạm đất: \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {{{40}^2} + {{30}^2}} = 50m/s\)
Câu 66 :
Một vật được ném ngang từ độ cao \(h\) ở nơi có gia tốc rơi tự do là \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \({v_0}\). Biết sau \(2s\), véctơ vận tốc của vật hợp với phương ngang góc \({30^0}\). Tốc độ ban đầu của vật gần nhất giá trị nào sau đây?
Đáp án : B Phương pháp giải :
+ Sử dụng phương trình vận tốc: - Theo phương Ox: \({v_x} = {v_0}\) - Theo phương Oy: \({v_y} = gt\) + Độ lớn của vận tốc tại vị trí bất kì: \(v = \sqrt {v_x^2 + v_y^2} \) + Vận dụng biểu thức liên hệ giữa \({v_x}\) và \({v_y}\): \(\tan \alpha = \frac{{{v_y}}}{{{v_x}}}\) Lời giải chi tiết :
+ Vận tốc của vật theo các phương : - Theo phương Ox: \({v_x} = {v_0}\) - Theo phương Oy: \({v_y} = gt\) + Theo đầu bài, ta có: \(\begin{array}{l}\tan \alpha = \frac{{{v_y}}}{{{v_x}}} \leftrightarrow \tan {30^0} = \frac{{gt}}{{{v_0}}}\\ \to {v_0} = \frac{{gt}}{{\tan {{30}^0}}} = \frac{{10.2}}{{\frac{1}{{\sqrt 3 }}}} = 20\sqrt 3 \left( {m/s} \right)\end{array}\)
Câu 67 :
Từ vị trí A, một vật được ném ngang với tốc độ \({v_0} = 2m/s\). Sau đó 1s, tại vị trí B có cùng độ cao với A người ta ném thẳng đứng một vật xuống dưới với tốc độ ban đầu \({v_0}'\). Biết \(AB = 6m\) và hai vật gặp nhau trong quá trình chuyển động. Lấy \(g = 10m/{s^2}\). Vận tốc \({v_0}'\) gần nhất với giá trị nào sau đây?
Đáp án : D Phương pháp giải :
+ Sử dụng phương trình chuyển động của vật ném ngang : \(x = {v_0}t\)và \({y_1} = \dfrac{1}{2}g{t^2}\) + Sử dụng phương trình chuyển động của vật được ném thẳng đứng :\({y_2} = {v_0}'(t + 1) - \dfrac{1}{2}g{(t + 1)^2}\) Lời giải chi tiết :
Chọn gốc thời gian là lúc ném vật nằm ngang Phương trình chuyển động của vật ném ngang theo phương ox:\(x = {v_0}t\) Phương trình chuyển động của vật ném ngang theo phương oy:\({y_1} = \dfrac{1}{2}g{t^2}\) Phương trình chuyển động của vật được ném thẳng đứng :\({y_2} = {v_0}'(t + 1) - \dfrac{1}{2}g{(t + 1)^2}\) Hai vật gặp nhau trong quá trình chuyển động: \( \to x = {v_0}t = AB \to t = \dfrac{{AB}}{{{v_0}}} = 3{\rm{s}}\) \( \to {{\rm{y}}_1} = {y_2} \leftrightarrow \dfrac{1}{2}g{t^2} = {v_0}'(t + 1) - \dfrac{1}{2}g{(t + 1)^2}\) \( \to {v_0}' = \dfrac{{g(t + 0,5)}}{{t + 1}} = \dfrac{{10(3 + 0,5)}}{{3 + 1}} = 8,75m/s\)
Câu 68 :
Ném vật theo phương ngang với vận tốc 10 m/s từ độ cao 40 m xuống đất. Lấy g = 10 m/s2. Phương trình quỹ đạo của vật và toạ độ của vật sau 2s là:
Đáp án : C Phương pháp giải :
+ Phương trình chuyển động của vật ném ngang: \(\left\{ \begin{array}{l}x = {v_0}t\,\,\,\,\,\,\,\,\left( 1 \right)\\y = \dfrac{1}{2}g{t^2}\,\,\,\left( 2 \right)\end{array} \right.\) + Phương trình quỹ đạo: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}\) Lời giải chi tiết :
Ta có: \(g = 10m/{s^2};{\rm{ }}h = 40{\rm{ }}m;{\rm{ }}{v_0}\; = 10{\rm{ }}m/s\) + Phương trình quỹ đạo: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \dfrac{{10}}{{{{2.10}^2}}}.{x^2} = \dfrac{{{x^2}}}{{20}}\,\,\left( m \right)\) + Toạ độ của vật sau 2s là: \(\left\{ \begin{array}{l}x = {v_0}t = 10.2 = 20m\\y = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}{.10.2^2} = 20m\end{array} \right.\)
Câu 69 :
Bi A có khối lượng gấp đôi bi B. Cùng một lúc tại tầng 3 trường THPT Trần Quốc Tuấn, bi A được thả rơi tự do, bi B được ném theo phương ngang (bỏ qua mọi lực cản) thì:
Đáp án : B Phương pháp giải :
Thời gian chuyển động của vật ném ngang bằng thời gian của vật được thả từ cùng độ cao: \(t = \sqrt {\dfrac{{2h}}{g}} \) Lời giải chi tiết :
Bi A được thả rơi và bi B được ném theo phương ngang ở cùng độ cao (tại tầng 3 trường THPT Trần Quốc Tuấn) nên cả hai cùng chạm đất một lúc.
Câu 70 :
Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao 180cm. Khi ra khỏi mép, nó rơi xuống nền nhà tại điểm cách mép bàn 90cm (theo phương ngang). Lấy \(g = 10m/{s^2}\). Tính vận tốc của bi lúc rời khỏi bàn và viết phương trình quỹ đạo của viên bi.
Đáp án : B Phương pháp giải :
+ Tầm ném xa của vật ném ngang: \(L = {v_0}t = {v_0}.\sqrt {\dfrac{{2h}}{g}} \) + Phương trình quỹ đạo của vật ném ngang: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}h = 180cm = 1,8m\\L = 90cm = 0,9m\\g = 10m/{s^2}\end{array} \right.\) Chuyển động của hòn bi khi rời khỏi mặt bàn coi như là chuyển động ném ngang với độ cao ban đầu \(h = 1,8m\) và có tầm ném xa là \(L = 0,9m\). Áp dụng công thức tính tầm ném xa ta có: \(L = {v_0}.\sqrt {\dfrac{{2h}}{g}} \Rightarrow {v_0} = \dfrac{L}{{\sqrt {\dfrac{{2h}}{g}} }} = \dfrac{{0,9}}{{\sqrt {\dfrac{{2.1,8}}{{10}}} }} = 1,5m/s\) Phương trình quỹ đạo của viên bi: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \left( {\dfrac{{10}}{{2.1,{5^2}}}} \right).{x^2} = \dfrac{{20}}{9}{x^2}\,\left( m \right)\)
Câu 71 :
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao \(h\) so với mặt đất. Chọn hệ trục toạ độ \(Oxy\) sao cho gốc O trùng với vị trí ném, Ox theo chiều \(\overrightarrow {{v_0}} \), Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc bắt đầu ném. Phương trình quỹ đạo của vật là: (với \(g = 10m/{s^2}\) )
Đáp án : C Phương pháp giải :
Phương trình quỹ đạo của vật ném ngang: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}{v_0} = 10m/s\\g = 10m/{s^2}\end{array} \right.\) \( \Rightarrow \) Phương trình quỹ đạo của vật: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \left( {\dfrac{{10}}{{{{2.10}^2}}}} \right).{x^2} = 0,05.{x^2}\)
Câu 72 :
Chuyển động ném ngang là gì?
Đáp án : D Phương pháp giải :
Vận dụng lí thuyết trang 49 bài 12 sách giáo khoa vật lí 10 Lời giải chi tiết :
Chuyển động ném ngang là chuyển động có vận tốc ban đầu theo phương nằm ngang và chuyển động dưới tác dụng của trọng lực.
Câu 73 :
Chuyển động nào sau đây là chuyển động ném ngang?
Đáp án : C Phương pháp giải :
Chuyển động ném ngang là chuyển động có vận tốc ban đầu theo phương nằm ngang và chuyển động dưới tác dụng của trọng lực. Lời giải chi tiết :
Trong câu A và B, chuyển động của vật chỉ dưới tác dụng của trọng lực nhưng vận tốc của vật không theo phương nằm ngang mà theo phương thẳng đứng => A, B, D sai
Câu 74 :
Trong chuyển động ném ngang, thành phần chuyển động theo phương thẳng đứng là chuyển động gì?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
+ Nếu bỏ qua sức cản của không khí thì chuyển động thành phần theo phương thẳng đứng của vật là chuyển động rơi tự do + Mặt khác, chuyển động rơi tự do là chuyển động nhanh dần
Câu 75 :
Trong chuyển động ném ngang, thành phần chuyển động theo phương nằm ngang là chuyển động gì?
Đáp án : C Phương pháp giải :
Vận dụng lí thuyết trong sách giáo khoa Lời giải chi tiết :
Trong chuyển động ném ngang, thành phần chuyển động theo phương nằm ngang là chuyển động thẳng đều.
Câu 76 :
Tầm xa không phụ thuộc vào đại lượng nào?
Đáp án : D Phương pháp giải :
Biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2.H}}{g}} \) Lời giải chi tiết :
Từ biểu thức tính tầm xa \(L = {v_0}\sqrt {\frac{{2.H}}{g}} \) => Tầm xa phụ thuộc vào: vận tốc ném, độ cao, gia tốc trọng trường => Tầm xa không phụ thuộc vào khối lượng
Câu 77 :
Nếu ném từ độ cao khác nhau ném ngang các vật với cùng vận tốc thì:
Đáp án : B Phương pháp giải :
Biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2.H}}{g}} \) Lời giải chi tiết :
Từ biểu thức tính tầm xa: \(L = {v_0}\sqrt {\frac{{2.H}}{g}} \), ta có tầm xa tỉ lệ với căn bậc 2 của độ cao => Với cùng vận tốc thì vật nào có độ cao lớn hơn thì tầm xa lớn hơn
|



















Danh sách bình luận