Trắc nghiệm Bài 1. Năng lượng và công - Vật Lí 10 Cánh diềuĐề bài
Câu 1 :
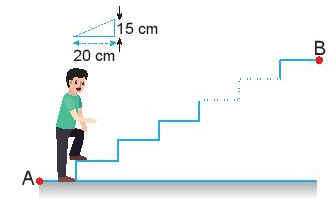
Một bạn học sinh có khối lượng 50 kg đi lên một cầu thang gồm 20 bậc cao 15 cm, dài 20 cm. Tính công tối thiểu mà bạn ấy phải thực hiện. Coi lực mà học sinh tác dụng lên mỗi bậc thang là không đổi trong quá trình di chuyển. Lấy gia tốc trọng trường là g = 10 m/s2
Câu 2 :
Khi rửa gầm xe ô tô, người ta sử dụng máy nâng ô tô lên độ cao h = 160 cm so với mặt sàn. Cho biết khối lượng ô tô là m = 1,5 tấn và gia tốc trọng trường là g = 10 m/s2 . Công tối thiểu mà máy nâng đã thực hiện được là bao nhiêu?
Câu 3 :
Dưới tác dụng của lực kéo \(\overrightarrow F \) có độ lớn 5 N, vật đi được quãng đường là 2 m theo hướng của lực \(\overrightarrow F \). Công của lực \(\overrightarrow F \) có độ lớn là:
Câu 4 :
Một cần cẩu nâng một vật có khối lượng 3 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao 15 m với gia tốc 1 m/s2 . Lấy g = 10 m/s2 . Công mà cần cẩu thực hiện được là bao nhiêu?
Câu 5 :
Khi kéo một vật trượt trên mặt phẳng nghiêng, lực tác dụng vào vật nhưng không sinh công là
Câu 6 :
Đơn vị nào sau đây không phải là của công?
Câu 7 :
Pin mặt trời đã có sự chuyển hóa dạng năng lượng nào?
Câu 8 :
Khi ném quả bóng từ mặt đất lên đến độ cao cực đại, đã có sự chuyển hóa năng lượng nào?
Câu 9 :
Đại lượng nào sau đây không phải là một dạng năng lượng?
Câu 10 :
Một ô tô khối lượng 10 tấn đang chạy với vận tốc 54 km/h trên đoạn đường phẳng ngang thì bắt đầu chuyển động chậm dần đều cho tới khi bị dừng lại do tác dụng của lực ma sát với mặt đường. Cho biết hệ số ma sát là 0,3. Lấy g = 10 m/s2. Công của lực ma sát trong khoảng thời gian chuyển động thẳng chậm dần đều là:
Câu 11 :
Một chiếc ô tô sau khi tắt máy còn đi được 100m. Biết ô tô nặng 1,5 tấn, hệ số cản bằng 0,25 (Lấy g = 10m/s2). Công của lực cản có giá trị là:
Câu 12 :
Một lực 2500 N tác dụng theo phương ngang được đặt lên một chiếc xe có khối lượng 500kg đang đứng yên trên một mặt phẳng ngang. Biết tổng lực cản chuyển động luôn là 1000N. Công của chiếc xe sau khi chuyển động được 2s là :
Câu 13 :
Cho hệ như hình vẽ: 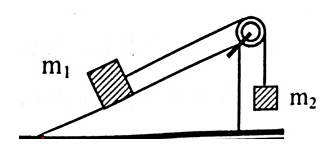 Biết \(\alpha = {30^0}\), \({m_1} = 1kg;{m_2} - 2kg\). Công của trọng lực của hệ thống khi \({m_1}\) đi lên không ma sát trên mặt phẳng nghiêng được quãng đường \(1m\).
Câu 14 :
Một động cơ điện cung cấp công suất $15 kW$ cho một cần cẩu nâng $1000 kg$ lên cao $30 m$. Lấy $g = 10 m/s^2$. Thời gian tối thiểu để thực hiện công việc đó là:
Câu 15 :
Một thang máy khối lượng $1$ tấn chở các hành khách có tổng khối lượng là $800 kg$. Khi chuyển động thanh máy còn chịu một lực cản không đổi bằng $4.10^3 N$. Để đưa thang máy lên cao với vận tốc không đổi $3 m/s$ thì công suất của động cơ phải bằng (cho $g =9,8 m/s^2$)
Câu 16 :
Một xe tải chạy đều trên đường ngang với tốc độ \(54 km/h\). Khi đến quãng đường dốc, lực cản tác dụng lên xe tăng gấp ba nhưng công suất của động cơ chỉ tăng lên được hai lần. Tốc độ chuyển động đều của xe trên đường dốc là:
Câu 17 :
Một máy bay khối lượng 3000kg khi cất cánh phải mất 80s để bay lên tới độ cao 1500m. Lấy g = 9,8m/s2. Xác định công suất của động cơ máy bay. Cho rằng công mà động cơ máy bay sinh ra lúc này chủ yếu là để nâng máy bay lên cao.
Câu 18 :
Một chiếc xe có khối lượng 1,1 tấn bắt đầu chạy với vận tốc bằng không với gia tốc là 4,6m/s2 trong thời gian 5s. Công suất trung bình của xe bằng:
Câu 19 :
Một ô tô đang leo dốc, nếu công suất của động cơ không đổi thì vận tốc của ô tô sẽ giảm đi vì:
Câu 20 :
Một cần cẩu nâng một vật có khối lượng 2 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao \(12,5m\) với gia tốc \(1m/{s^.}^2\). Lấy \(g = 10m/{s^2}\). Hãy tính công mà cần cầu thực hiện và công suất trung bình của cần cẩu ấy.
Câu 21 :
Biểu thức đúng tính công suất là?
Câu 22 :
Đơn vị của công suất nào sau đây đúng?
Câu 23 :
Đại lượng đặc trưng cho khả năng sinh công nhanh hay chậm là?
Câu 24 :
Một vật trọng lượng 50 N được kéo thẳng đều từ mặt đất lên độ cao 10 m trong khoảng thời gian 1 phút 40 giây. Xác định công suất của lực kéo.
Câu 25 :
Một người kép một thùng nước 20 kg từ giếng sâu 5 m lên trong 10 s. Công suất của người kéo là bao nhiêu? Biết thùng nước chuyển động đều và lấy g = 10 m/s2
Câu 26 :
Động cơ của một thang máy tác dụng lực kéo 15000 N để thang máy chuyển động thẳng đều lên trên trong 6 s và quãng đường đi được tương ứng là 15 m. Công suất trung bình của động cơ là bao nhiêu?
Câu 27 :
Một ô tô có khối lượng là 4 tấn đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc 10 m/s, công suất của động cơ ô tô là 20 kW. Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường 250 m thì vận tốc của ô tô tăng lên đến 54 km/h. Công suất trung bình của động cơ ô tô trên quãng đường này là bao nhiêu? Lấy g = 10 m/s2
Câu 28 :
Cho một vật có khối lượng 8 kg rơi tự do. Tính công suất trung bình của vật trong giây thứ tư. Lấy g = 10 m/s2
Lời giải và đáp án
Câu 1 :
Một bạn học sinh có khối lượng 50 kg đi lên một cầu thang gồm 20 bậc cao 15 cm, dài 20 cm. Tính công tối thiểu mà bạn ấy phải thực hiện. Coi lực mà học sinh tác dụng lên mỗi bậc thang là không đổi trong quá trình di chuyển. Lấy gia tốc trọng trường là g = 10 m/s2
Đáp án : A Phương pháp giải :
Công thức tính công: \(A = F.s.\cos (\overrightarrow F ;\overrightarrow s )\) Lời giải chi tiết :
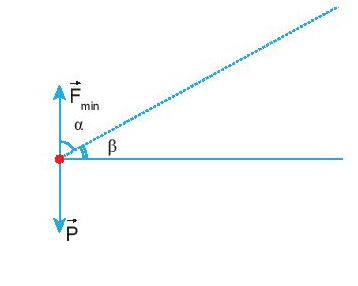
Muốn lên cầu thang này bạn học sinh phải có lực nâng tối thiểu là: \(\begin{array}{l}{\overrightarrow F _{\min }} = - \overrightarrow P \\ \Rightarrow {F_{\min }} = P = m.g\end{array}\) Độ dịch chuyển của bạn học sinh là: \(\overrightarrow d = \overrightarrow {AB} \) => Công tối thiểu mà bạn ấy phải thực hiện là: \(\begin{array}{l}{A_{\min }} = {F_{\min }}.d.\cos \alpha = {F_{\min }}.d.\sin \beta \\ = m.g.d.\sin \beta = m.g.h = 50.10.20.0,15 = 1500(J)\end{array}\)
Câu 2 :
Khi rửa gầm xe ô tô, người ta sử dụng máy nâng ô tô lên độ cao h = 160 cm so với mặt sàn. Cho biết khối lượng ô tô là m = 1,5 tấn và gia tốc trọng trường là g = 10 m/s2 . Công tối thiểu mà máy nâng đã thực hiện được là bao nhiêu?
Đáp án : B Phương pháp giải :
Công thức tính công: \(A = F.s.\cos (\overrightarrow F ;\overrightarrow s )\) Lời giải chi tiết :
Để nâng được ô tô lên máy nâng phải tác dụng vào ô tô lực tối thiểu: \(\begin{array}{l}{\overrightarrow F _{\min }} = - \overrightarrow P \\ \Rightarrow {F_{\min }} = P = m.g = 1,{5.10^3}.10 = 1,{5.10^4}(N)\end{array}\) Công tối thiểu mà máy nâng đã thực hiện được là: A = P.h = 1,5.104 .0,16 = 24000 (J) = 24 (kJ)
Câu 3 :
Dưới tác dụng của lực kéo \(\overrightarrow F \) có độ lớn 5 N, vật đi được quãng đường là 2 m theo hướng của lực \(\overrightarrow F \). Công của lực \(\overrightarrow F \) có độ lớn là:
Đáp án : D Phương pháp giải :
Công thức tính công: \(A = F.s.\cos (\overrightarrow F ;\overrightarrow s )\) Lời giải chi tiết :
Vật dịch chuyển theo hướng của lực nên α = 0 => Công của lực \(\overrightarrow F \) có độ lớn là: A = F.s.cosα = 5.2.cos00 = 10 J
Câu 4 :
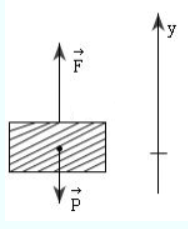
Một cần cẩu nâng một vật có khối lượng 3 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao 15 m với gia tốc 1 m/s2 . Lấy g = 10 m/s2 . Công mà cần cẩu thực hiện được là bao nhiêu?
Đáp án : B Phương pháp giải :
Công thức tính công: \(A = F.s.\cos (\overrightarrow F ;\overrightarrow s )\) Lời giải chi tiết :
Áp dụng định luật II Newton ta có: \(\overrightarrow F + \overrightarrow P = m.\overrightarrow a \) (*) Chiếu (*) lên Oy ta có: F – P = m.a => F = P + m.a = m. (g + a) = 3000. (10 + 1 ) = 33000 (N) Công mà cần cẩu thực hiện được là: A = F.s.cos00 = 33000.15.1 = 495 000 (J)
Câu 5 :
Khi kéo một vật trượt trên mặt phẳng nghiêng, lực tác dụng vào vật nhưng không sinh công là
Đáp án : B Phương pháp giải :
Biểu thức tính công là: A = F.s.cosα + \(0 \le \alpha < {90^0}\) thì A > 0, công phát động + \(\alpha = {90^0}\) thì A = 0, lực không sinh công + \({90^0} < \alpha \le {180^0}\) thì A < 0, công cản Với α là góc hợp bởi \(\overrightarrow F \)và chiều chuyển động của vật Lời giải chi tiết :
Khi kéo vật trượt trên mặt phẳng nghiêng, phản lực N vuông góc với chiều chuyển động nên phản lực không sinh công
Câu 6 :
Đơn vị nào sau đây không phải là của công?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Trong hệ SI, đơn vị của công là “J” Ngoài ra công còn một số đơn vị khác như: cal; kcal; W.s W là đơn vị của công suất
Câu 7 :
Pin mặt trời đã có sự chuyển hóa dạng năng lượng nào?
Đáp án : B Phương pháp giải :
Vận dụng kiến thức đã học và liên hệ thực tiễn Lời giải chi tiết :
Pin mặt trời đã có sự chuyển hóa năng lượng quang năng thành điện năng
Câu 8 :
Khi ném quả bóng từ mặt đất lên đến độ cao cực đại, đã có sự chuyển hóa năng lượng nào?
Đáp án : B Phương pháp giải :
Cơ năng không đổi trong suốt quá trình chuyển động Lời giải chi tiết :
Chọn thế năng tại mặt đất, khi chuyển động lên đến độ cao cực đại, thì động năng đã chuyển hóa thành thế năng
Câu 9 :
Đại lượng nào sau đây không phải là một dạng năng lượng?
Đáp án : D Phương pháp giải :
Mọi hiện tượng xảy ra trong tự nhiên đều cần có năng lượng dưới các dạng khác nhau như: cơ năng, hóa năng, nhiệt năng, điện năng, năng lượng ánh sáng, năng lượng âm thanh, năng lượng nguyên tử Lời giải chi tiết :
Đại lượng không phải là một dạng năng lượng là “Nhiệt lượng”
Câu 10 :
Một ô tô khối lượng 10 tấn đang chạy với vận tốc 54 km/h trên đoạn đường phẳng ngang thì bắt đầu chuyển động chậm dần đều cho tới khi bị dừng lại do tác dụng của lực ma sát với mặt đường. Cho biết hệ số ma sát là 0,3. Lấy g = 10 m/s2. Công của lực ma sát trong khoảng thời gian chuyển động thẳng chậm dần đều là:
Đáp án : B Phương pháp giải :
+ Định luật II Niuton: \(\overrightarrow F = m\overrightarrow a \) + Độ lớn lực ma sát: \({F_{ms}} = \mu N = \mu mg\) + Công thức liên hệ giữa s, v, a: \({v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}}\) + Công thức tính công: \(A = F.s.\cos \alpha \) Lời giải chi tiết :
+ Ta có: \(\left\{ \begin{array}{l}m = 10T = 10\,000kg\\{v_0} = 54km/h = 15m/s\\g = 10m/{s^2}\\\mu = 0,3\end{array} \right.\) + Theo định luật II Niu-tơn, gia tốc chuyển động chậm dần đều của ô tô có giá trị : \(a = \dfrac{{{F_{ms}}}}{m} = \dfrac{{ - \mu P}}{m} = - \mu g = - 0,3.10 = - 3\left( {m/{s^2}} \right)\) + Ta có: \({v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}}\) Khi ô tô dừng hẳn thì: \(v = 0 \Rightarrow s = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 3} \right)}} = 37,5m\) + Công của lực ma sát trong khoảng thời gian chuyển động thẳng chậm dần đều là: \(A = {F_{ms}}.s = ma.s = 10\,000.\left( { - 3} \right).37,5 = - 1125kJ\)
Câu 11 :
Một chiếc ô tô sau khi tắt máy còn đi được 100m. Biết ô tô nặng 1,5 tấn, hệ số cản bằng 0,25 (Lấy g = 10m/s2). Công của lực cản có giá trị là:
Đáp án : C Phương pháp giải :
Công thức tính công: \(A = F.s.\cos \alpha ;\,\,\alpha = \left( {\overrightarrow F ;\overrightarrow s } \right)\) Lời giải chi tiết :
Độ lớn của lực cản tác dụng lên xe: \({F_c} = {F_{ms}} = \mu mg = 0,25.1,5.1000.10 = 3750N\) Công của lực cản tác dụng lên xe: \(A = {F_c}.s.\cos \left( {\overrightarrow {{F_c}} ;\overrightarrow s } \right) = 3750.100\cos 180 = - 375000J = - 375kJ\)
Câu 12 :
Một lực 2500 N tác dụng theo phương ngang được đặt lên một chiếc xe có khối lượng 500kg đang đứng yên trên một mặt phẳng ngang. Biết tổng lực cản chuyển động luôn là 1000N. Công của chiếc xe sau khi chuyển động được 2s là :
Đáp án : D Phương pháp giải :
Áp dụng phương trình định luật II Niuton tính gia tốc của xe. Quãng đường xe đi được sau 2s là: \(s = {v_0}t + \dfrac{1}{2}a{t^2}\) Công của chiếc xe: \(A = F.s.\cos \alpha \) Lời giải chi tiết :
Lực tổng hợp tác dụng lên xe: \({F_T} = F - {F_c} = 2500 - 1000 = 1500N\) Ta có: \(a = \dfrac{{{F_T}}}{m} = \dfrac{{1500}}{{500}} = 3m/{s^2}\) Quãng đường xe đi được sau 2s: \(s = {v_0}t + \dfrac{1}{2}a{t^2} = 0 + \dfrac{1}{2}{.3.2^2} = 6m\) Công của chiếc xe sau khi chuyển động được 2s là : \(A = {F_T}.s.\cos \alpha = 1500.6.\cos 0 = 9000J = 9kJ\)
Câu 13 :
Cho hệ như hình vẽ:  Biết \(\alpha = {30^0}\), \({m_1} = 1kg;{m_2} - 2kg\). Công của trọng lực của hệ thống khi \({m_1}\) đi lên không ma sát trên mặt phẳng nghiêng được quãng đường \(1m\).
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính công: \(A = Fscos\alpha \) Lời giải chi tiết :
Ta có, khi \({m_1}\) đi lên quãng đường \(s = 1m\) trên mặt phẳng nghiêng thì \({m_2}\) đi xuống thẳng đứng một quãng đường cũng bằng \(s\) 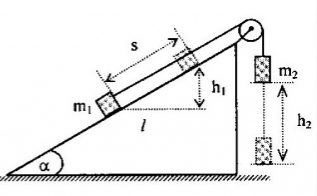 Ta có: \(\begin{array}{l}{h_1} = s.\sin \alpha = 1.\sin {30^0} = 0,5m\\{h_2} = s = 1m\end{array}\) Trọng lực \(\overrightarrow {{P_1}} \) có hướng ngược với hướng chuyển dời của vật 1 => Công của trọng lực của vật 1: \({A_1} = {P_1}.{h_1}.cos{180^0} = - {m_1}g{h_1}\) Trọng lực \(\overrightarrow {{P_2}} \) có cùng hướng với hướng chuyển dời của vật 2 => Công của trọng lực của vật 2: \({A_2} = {P_2}{h_2} = {m_2}gh\) Công của trọng lực của hệ thống: \(\begin{array}{l}A = {A_1} + {A_2} = - {m_1}g{h_1} + {m_2}g{h_2}\\ = - 1.10.0,5 + 2.10.1 = 15J\end{array}\)
Câu 14 :
Một động cơ điện cung cấp công suất $15 kW$ cho một cần cẩu nâng $1000 kg$ lên cao $30 m$. Lấy $g = 10 m/s^2$. Thời gian tối thiểu để thực hiện công việc đó là:
Đáp án : B Phương pháp giải :
+ Vận dụng biểu thức tính công: \(A = F{\rm{scos}}\alpha \) + Vận dụng biểu thức tính công suất: \(P = \dfrac{A}{t}\) Lời giải chi tiết :
Ta có: + Công \(A = Fs\cos \alpha = P.h = mgh\) + Công suất: \(P = \dfrac{A}{t} \to t = \dfrac{A}{P}\) => Thời gian tối thiểu để thực hiện công việc đó là: \(t = \dfrac{A}{P} = \dfrac{{mgh}}{P} = \dfrac{{1000.10.30}}{{{{15.10}^3}}} = 20s\)
Câu 15 :
Một thang máy khối lượng $1$ tấn chở các hành khách có tổng khối lượng là $800 kg$. Khi chuyển động thanh máy còn chịu một lực cản không đổi bằng $4.10^3 N$. Để đưa thang máy lên cao với vận tốc không đổi $3 m/s$ thì công suất của động cơ phải bằng (cho $g =9,8 m/s^2$)
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính công suất: \(P = \dfrac{A}{t} = F\dfrac{s}{t} = Fv\) Lời giải chi tiết :
Để thang máy chuyển động với vận tốc không đổi thì F = P + Fc Công suất: P=Fv=(Mg + Fc)v = ((mthang + mtải)g + Fc)v = ((1000 + 800).9,8 + 4000).3 = 64920 W
Câu 16 :
Một xe tải chạy đều trên đường ngang với tốc độ \(54 km/h\). Khi đến quãng đường dốc, lực cản tác dụng lên xe tăng gấp ba nhưng công suất của động cơ chỉ tăng lên được hai lần. Tốc độ chuyển động đều của xe trên đường dốc là:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính công suất: \(P = \dfrac{A}{t} = F\dfrac{s}{t} = Fv\) Lời giải chi tiết :
Do xe chạy đều nên \(F = F_c\) \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{F_1}{v_1}}}{{{F_2}{v_2}}} = > {v_2} = \dfrac{{{P_2}{F_1}{v_1}}}{{{P_1}{F_2}}}\) Theo đề bài \({F_2} = 3{F_1};\,{P_2} = 2{P_1} = > {v_2} = 10\,m/s\)
Câu 17 :
Một máy bay khối lượng 3000kg khi cất cánh phải mất 80s để bay lên tới độ cao 1500m. Lấy g = 9,8m/s2. Xác định công suất của động cơ máy bay. Cho rằng công mà động cơ máy bay sinh ra lúc này chủ yếu là để nâng máy bay lên cao.
Đáp án : A Phương pháp giải :
+ Công thức tính công: \(A = F.s.\cos \alpha \) + Công suất: \(P = \dfrac{A}{t}\) Lời giải chi tiết :
Lực nâng máy bay lên cao phải có độ lớn bằng trọng lượng của máy bay : \(F = P = mg = 3000.9,8 = 29400{\rm{ }}N\) Do đó, động cợ máy bay phải thực hiện công : \(A = F.h = 29400.1500 = 44,{1.10^6}{\rm{ }}J\) Suy ra công suất của động cơ máy bay : \({P_{dc}} = \dfrac{A}{t} = \dfrac{{44,{{1.10}^6}}}{{80}} = 551,25\left( {kW} \right)\)
Câu 18 :
Một chiếc xe có khối lượng 1,1 tấn bắt đầu chạy với vận tốc bằng không với gia tốc là 4,6m/s2 trong thời gian 5s. Công suất trung bình của xe bằng:
Đáp án : C Phương pháp giải :
Công suất trung bình P = A/t Công của lực tác dụng A = Fscosα Quãng đường đi được trong chuyển động biến đổi đều s = v0t + 0,5at2 Biểu thức định luật 2 Niu tơn: F = ma Lời giải chi tiết :
Lực kéo tác dụng lên xe: F = ma = 1100.4,6 = 5060N Quãng đường xe đi được: s = v0t + 0,5at2 = 0,5.4,6.52 = 57,5m Công của lực kéo: A = Fscosα = 5060.57,5.cos0 = 290950J Công suất trung bình của động cơ: \(P=\frac{A}{t}=\frac{290950}{5}={{5,82.10}^{4}}\text{W}\)
Câu 19 :
Một ô tô đang leo dốc, nếu công suất của động cơ không đổi thì vận tốc của ô tô sẽ giảm đi vì:
Đáp án : A Phương pháp giải :
Công thức tính công suất: \(P = \dfrac{A}{t} = \dfrac{{F.s}}{t} = F.v\) Lời giải chi tiết :
Ta có: \(P = F.v\) \( \Rightarrow \) v giảm thì F tăng. \( \Rightarrow \) Một ô tô đang leo dốc, nếu công suất của động cơ không đổi thì vận tốc của ô tô sẽ giảm đi để tăng lực kéo giúp ô tô leo được dốc.
Câu 20 :
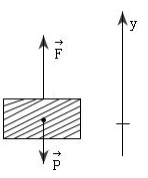
Một cần cẩu nâng một vật có khối lượng 2 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao \(12,5m\) với gia tốc \(1m/{s^.}^2\). Lấy \(g = 10m/{s^2}\). Hãy tính công mà cần cầu thực hiện và công suất trung bình của cần cẩu ấy.
Đáp án : A Phương pháp giải :
Sử dụng định luật II Niuton tính được lực kéo thang máy. Công thức tính công của lực: \(A = F.s.cos\left( {\overrightarrow F ;\overrightarrow s } \right)\) Công thức tính quãng đường: \(s = {v_0}t + \dfrac{1}{2}a{t^2} \Rightarrow t\) Công thức tính công suất: \(P = \dfrac{A}{t}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}m = 2T = 2000kg\\s = h = 12,5m\\a = 1m/{s^2}\\g = 10m/{s^2}\end{array} \right.\) Biểu diễn các lực tác dụng vào thang máy trên hình: Áp dụng định luật II Niuton ta có: \(\overrightarrow F + \overrightarrow P = m.\overrightarrow a \,\,\left( * \right)\) Chiếu (*) lên Oy ta có: \(\begin{array}{l}F - P = ma \Rightarrow F = P + ma = m\left( {g + a} \right)\\ \Rightarrow F = 2000.\left( {10 + 1} \right) = 22000N\end{array}\) Công mà cần cẩu thực hiện: \(A = F.s = 22000.12,5 = 275000J\) Lại có quãng đường vật đi được trong 12,5m là: \(s = {v_0}t + \dfrac{1}{2}a{t^2} \Leftrightarrow 12,5 = 0 + \dfrac{1}{2}.1.{t^2} \Rightarrow t = 5s\) Công suất trung bình của cần cẩu: \(P = \dfrac{A}{t} = \dfrac{{275000}}{5} = 55000W = 55kW\)
Câu 21 :
Biểu thức đúng tính công suất là?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Biểu thức tính công suất: P = A/t Trong đó: + P: Công suất (W) + A: Công thực hiện được (J) + t: Thời gian vật thực hiện (s)
Câu 22 :
Đơn vị của công suất nào sau đây đúng?
Đáp án : A Phương pháp giải :
Vận dụng kiến thức trong sách giáo khoa Lời giải chi tiết :
Cal, J, W.h là đơn vị của công Đơn vị của P là W, ngoài ra công suất còn có đơn vị là J/s
Câu 23 :
Đại lượng đặc trưng cho khả năng sinh công nhanh hay chậm là?
Đáp án : B Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Đại lượng đặc trưng cho khả năng sinh công nhanh hay chậm của người hoặc thiệt sinh công, được gọi là công suất hay tốc độ sinh công.
Câu 24 :
Một vật trọng lượng 50 N được kéo thẳng đều từ mặt đất lên độ cao 10 m trong khoảng thời gian 1 phút 40 giây. Xác định công suất của lực kéo.
Đáp án : C Phương pháp giải :
Áp dụng công thức: A = W = mgh = P.h P = A/t Lời giải chi tiết :
Ta có: A = W = mgh = P.h = 50.10 = 500 J Đổi t = 1 phút 40 giây = 100 (s) => Công suất của lực kéo là: \(P = \frac{A}{t} = \frac{{500}}{{100}} = 5(W)\)
Câu 25 :
Một người kép một thùng nước 20 kg từ giếng sâu 5 m lên trong 10 s. Công suất của người kéo là bao nhiêu? Biết thùng nước chuyển động đều và lấy g = 10 m/s2
Đáp án : B Phương pháp giải :
Áp dụng các biểu thức: + \(v = \frac{s}{t}\) + P = F.v Lời giải chi tiết :
Vì vật chuyển động thẳng đều nên tốc độ của vật là: \(v = \frac{s}{t} = \frac{5}{{10}} = 0,5(m/s)\) Lực kéo vật lên trọng lượng của vật: F = m.g = 20.10 = 200 (N) Công suất của người kéo là: P = F.v = 200.0,5 = 100 (W)
Câu 26 :
Động cơ của một thang máy tác dụng lực kéo 15000 N để thang máy chuyển động thẳng đều lên trên trong 6 s và quãng đường đi được tương ứng là 15 m. Công suất trung bình của động cơ là bao nhiêu?
Đáp án : C Phương pháp giải :
Áp dụng các công thức + \(v = \frac{s}{t}\) + P = F.v Lời giải chi tiết :
Tốc độ của thang máy là: \(v = \frac{s}{t} = \frac{{15}}{6} = 2,5(m/s)\) Công suất trung bình của động cơ là: P = F.v = 15000.2,5 = 37500 (W)
Câu 27 :
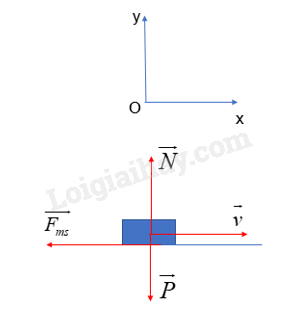
Một ô tô có khối lượng là 4 tấn đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc 10 m/s, công suất của động cơ ô tô là 20 kW. Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường 250 m thì vận tốc của ô tô tăng lên đến 54 km/h. Công suất trung bình của động cơ ô tô trên quãng đường này là bao nhiêu? Lấy g = 10 m/s2
Đáp án : D Phương pháp giải :
Áp dụng một số công thức: + Định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \) + Công thức chuyển động biến đổi đều: \(a = \frac{{{v^2} - v_0^2}}{{2.s}};v = {v_0} + at\) + Công thức tính vận tốc trung bình: \(\overline v = \frac{s}{t}\) + Công suất trung bình: \(\overline P = \overline v .t\) Lời giải chi tiết :
Đổi 54 km/h = 15 m/s; m = 4 tấn = 4000 kg. Gia tốc chuyển động của ô tô là: \(a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{{{15}^2} - {{10}^2}}}{{2.250}} = 0,25(m/{s^2})\)
Khi ô tô chuyển động đều, ta có: \(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_k}} + \overrightarrow {{F_{ms}}} = m.\overrightarrow a = \overrightarrow 0 \) (*) Chiếu (*) lên chiều dương của trục Ox, Oy, ta có: \(\begin{array}{l}\left\{ \begin{array}{l}N = P = m.g\\{F_k} - {F_{ms}} = 0\end{array} \right.\\ \Rightarrow {F_k} = {F_{ms}} = \mu .N = \mu mg\end{array}\) Mặt khác, ta có: \({P_{dc}} = {F_k}.v \Rightarrow {F_k} = \frac{{{P_{dc}}}}{v} = \frac{{20000}}{{10}} = 2000(N)\) Có: \({F_{ms}} = {F_k} \Leftrightarrow \mu mg = {F_k} \Rightarrow \mu = \frac{{{F_k}}}{{mg}} = \frac{{2000}}{{4000.10}} = 0,05\) Khi vật tăng tốc đến v = 15 m/s Theo định luật 2 Newton, ta có: \(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_k}} + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \) (**) Chiếu (**) lên chiều dương của trục Oy, ta có: \(N - P = 0 \Leftrightarrow N = P = mg\) Chiếu (**) lên chiều dương của trục Ox, ta có: \(\begin{array}{l}{F_k} - {F_{ms}} = m.a \Leftrightarrow {F_k} = {F_{ms}} + m.a\\ \Leftrightarrow {F_k} = \mu .N + m.a \Leftrightarrow {F_k} = \mu mg + ma\\ \Rightarrow {F_k} = 0,05.4000.10 + 4000.0,25 = 3000(N)\end{array}\) Thời gian ô tô tăng tốc là: \(t = \frac{{v - {v_0}}}{a} = \frac{{15 - 10}}{{0,25}} = 20(s)\) => Vận tốc trung bình của ô tô trên quãng đường đó là: \(\overline v = \frac{s}{t} = \frac{{250}}{{20}} = 12,5(m/s)\) => Công suất trung bình của động cơ ô tô trên quãng đường đó là: \(\overline P = {F_k}.\overline v = 3000.12,5 = 37500(W)\)
Câu 28 :
Cho một vật có khối lượng 8 kg rơi tự do. Tính công suất trung bình của vật trong giây thứ tư. Lấy g = 10 m/s2
Đáp án : A Phương pháp giải :
Áp dụng các công thức: + \(s = \frac{1}{2}g{t^2}\) + \(A = F.s.\cos (\overrightarrow F ;\overrightarrow s )\) + \(P = \frac{A}{t}\) Lời giải chi tiết :
Quãng đường vật rơi được trong 3 s là: \({s_3} = \frac{1}{2}.g.t_3^2 = \frac{1}{2}{.10.3^2} = 45(m)\) Quãng đường vật rơi được trong 4 s là: \({s_4} = \frac{1}{2}.g.t_4^2 = \frac{1}{2}{.10.4^2} = 80(m)\) => Quãng đường vật đi được trong giây thứ tư là: Δs = s4 – s3 = 80 – 45 = 35 (m) Công của trong lực trong giây thứ tư là: A = m.g.Δs = 8.10.35 = 2800 (J) => Công suất trung bình của vật trong giây thứ tư là: \(P = \frac{A}{t} = \frac{{2800}}{1} = 2800(W)\)
|



















Danh sách bình luận