Giải mục 2 trang 53, 54, 55 SGK Toán 12 tập 1 - Chân trời sáng tạoToạ độ của điểm và vectơ Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
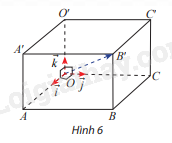
KP2 Trả lời câu hỏi Khám phá 2 trang 53 SGK Toán 12 Chân trời sáng tạo Cho hình hộp chữ nhật OABC.O′A′B′C′ có cạnh OA = 3, OC = 5, OO′ = 2. Vẽ ba vectơ đơn vị \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) lần lượt trên các cạnh OA, OC, OO′. Biểu diễn \(\overrightarrow {OB'} \) theo ba vectơ \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \)
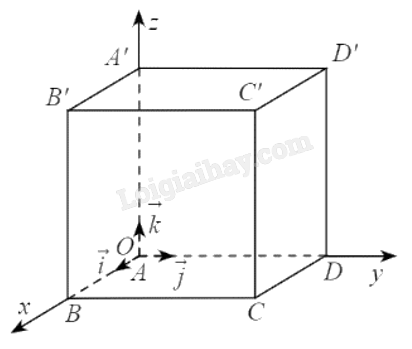
Phương pháp giải: Áp dụng quy tắc 3 điểm. Lời giải chi tiết: \(\overrightarrow {OB'} = \overrightarrow {OO'} + \overrightarrow {OB} = \overrightarrow {OO'} + \overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow k + 3\overrightarrow i + \overrightarrow {5j} \). TH2 Trả lời câu hỏi Thực hành 2 trang 54 SGK Toán 12 Chân trời sáng tạo Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 5. Chọn hệ trục toạ độ Oxyz có gốc toạ độ O trùng với A; các điểm B, D, A′ lần lượt nằm trên các tia Ox, Oy, Oz. Xác định toạ độ các điểm B, C, C′. Phương pháp giải: Vẽ hệ trục tọa độ và quan sát. Lời giải chi tiết:
Ta có: \(\overrightarrow {OB} = 5\overrightarrow i \Rightarrow B(5;0;0)\); \(\overrightarrow {OC} = 5\overrightarrow i + 5\overrightarrow j \Rightarrow C(5;5;0)\); \(\overrightarrow {OC'} = 5\overrightarrow i + 5\overrightarrow j + 5\overrightarrow k \Rightarrow C'(5;5; 5)\). KP3 Trả lời câu hỏi Khám phá 3 trang 54 SGK Toán 12 Chân trời sáng tạo Trong không gian Oxyz, cho vectơ \(\overrightarrow a \). Vẽ điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \). Gọi (\({a_1};{a_2};{a_3}\)) là toạ độ của điểm A. Hãy biểu diễn \(\overrightarrow a \) theo ba vectơ đơn vị \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \)
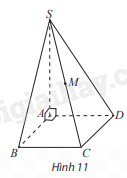
Phương pháp giải: Quan sát hình vẽ. Lời giải chi tiết: Ta có: \(\overrightarrow a \)= \({a_1}\overrightarrow i \)+\({a_2}\overrightarrow j \)+\({a_3}\overrightarrow k \). TH3 Trả lời câu hỏi Thực hành 3 trang 56 SGK Toán 12 Chân trời sáng tạo Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3 (Hình 11). a) Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ. b) Trong hệ toạ độ nói trên, tìm toạ độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AS} \) và \(\overrightarrow {AM} \) với M là trung điểm của cạnh SC.
Phương pháp giải: Vẽ hệ trục tọa độ và quan sát hình vẽ. Lời giải chi tiết: a)
Các vecto đơn vị của Ox, Oy, Oz lần lượt là \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \). b) \(\overrightarrow {AB} = 2\overrightarrow i \Rightarrow \overrightarrow {AB} = (2;0;0)\); \(\overrightarrow {AD} = 2\overrightarrow j \Rightarrow \overrightarrow {AD} = (0;2;0)\); \(\overrightarrow {AS} = 3\overrightarrow k \Rightarrow \overrightarrow {AS} (0;0;3)\). \(\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AS} + \overrightarrow {AC} ) \) \(= \frac{1}{2}(3\overrightarrow k + 2\overrightarrow i + 2\overrightarrow j ) \) \(= \overrightarrow i + \overrightarrow j + \frac{3}{2}\overrightarrow k \). \(\Rightarrow \overrightarrow {AM} = (1;1;\frac{3}{2})\). VD2 Trả lời câu hỏi Vận dụng 2 trang 56 SGK Toán 12 Chân trời sáng tạo Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14, \(\widehat {NOB} = 32^\circ \), \(\widehat {MOC} = 65^\circ \). Tìm toạ độ điểm M.
Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong các tam giác vuông để tìm hoành độ, tung độ, cao độ của M. Lời giải chi tiết: Xét tam giác COM vuông tại C: \(CO = OM.\cos 65^\circ = 14.\cos 65^\circ \approx 5,92\). \(CM = OM.\sin 65^\circ = 14.\sin 65^\circ \approx 12,69\). Xét tam giác BON vuông tại B: \(OB = ON.\cos 32^\circ = CM.\cos 32^\circ = 12,69.\cos 32^\circ \approx 10,76\). Xét tam giác AON vuông tại A: \(OA = ON.\cos (90^\circ - 32^\circ ) = 12,69.\cos 58^\circ = 6,72\). Vậy tọa độ của M là (6,72; 10,76; 5,92).
|























Danh sách bình luận