Giải mục 1 trang 32, 33 SGK Toán 12 tập 2 - Chân trời sáng tạo

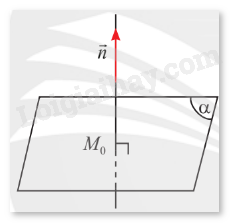
HĐ1

Trả lời câu hỏi Hoạt động 1 trang 32 SGK Toán 12 Chân trời sáng tạo

a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha  \right)\) vuông góc với giá của vectơ \(\vec n\)?

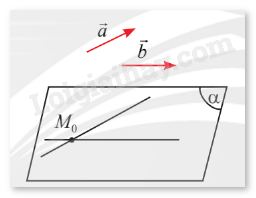
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha  \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?

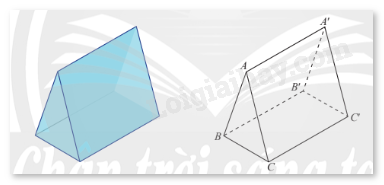
Phương pháp giải:

Sử dụng các kiến thức về đường thẳng vuông góc mặt phẳng, đường thẳng song song với mặt phẳng đã được học ở các lớp dưới.

Lời giải chi tiết:

a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha  \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).

b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta  \right)\) chứa \(a'\) và \(b\).

Nếu \({M_0} \in \left( \beta  \right)\) thì mặt phẳng \(\left( \beta  \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).

Nếu \({M_0} \notin \left( \beta  \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha  \right)\) đi qua \({M_0}\) và song song với \(\left( \beta  \right)\). Khi đó, \(\left( \alpha  \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).

VD1

Trả lời câu hỏi Vận dụng 1 trang 33 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).

a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).

b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).

Phương pháp giải:

a) Chỉ ra 2 vectơ không cùng phương và có giá song song hoặc nằm trên mặt phẳng \(\left( {ABC} \right)\).

b) Chỉ ra 1 đường thẳng vuông góc với mặt phẳng \(\left( {OAB} \right)\), sau đó chọn 1 vectơ nằm trên mặt phẳng đó làm vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).

Lời giải chi tiết:

a) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).

b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).

Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).

Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).

TH1

Trả lời câu hỏi Thực hành 1 trang 33 SGK Toán 12 Chân trời sáng tạo

Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).

Phương pháp giải:

Để xác định một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \(\left( {A'B'C'} \right)\).

Để xác định một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra một đường thẳng vuông góc với \(\left( {A'B'C'} \right)\), sau đó chọn một vectơ có giá song song hoặc trùng với đường thẳng đó.

Lời giải chi tiết:

Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).

Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).

Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).