Giải mục 1 trang 26, 27, 28, 29 Chuyên đề học tập Toán 10 - Chân trời sáng tạoBằng cách tô màu trên lưới ô vuông như hình dưới đây Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Khám phá
Bằng cách tô màu trên lưới ô vuông như hình dưới đây,
Một học sinh phát hiện ra công thức sau: \(1 + 3 + 5 + ... + (2n - 1) = {n^2}\quad (1)\) a) Hãy chỉ ra công thức (1) đúng với \(n = 1,2,3,4,5.\) b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên \(n \ge 1\). Khẳng định như vậy đã thuyết phục chưa? Tại sao? Lời giải chi tiết: a) Kiểm tra bằng tính toán trực tiếp. Ta có \(1 = {1^2}\) nên (1) đúng với \(n = 1\) \(1 + 3 = 4 = {2^2}\) nên (1) đúng với \(n = 2\) \(1 + 3 + 5 = 9 = {3^2}\) nên (1) đúng với \(n = 3\) \(1 + 3 + 5 + 7 = 16 = {4^2}\) nên (1) đúng với \(n = 4\) \(1 + 3 + 5 + 7 + 9 = 25 = {5^2}\) nên (1) đúng với \(n = 5\) b) Khẳng định của bạn HS chỉ là phỏng đoán. Việc tô màu hay tính toán trực tiếp không thể kiểm chứng hết tất cả các giá trị của n (mà chỉ kiểm chứng được một số hữu hạn giá trị n nào đó). Do đó khẳng định của bạn HS là chưa thuyết phục. Thực hành 1 Chứng minh rằng đẳng thức sau đúng với mọi \(n \in \mathbb{N}*\) \(1 + 2 + 3 + ... + n = \frac{{n(n + 1)}}{2}\) Phương pháp giải: Chứng minh mệnh đề đúng với \(n \ge p\) thì: Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\) Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận. Lời giải chi tiết: Ta chứng minh bằng quy nạp theo n. Bước 1: Với \(n = 1\) ta có \(1 = \frac{{1(1 + 1)}}{2}\) Như vậy mệnh đề đúng cho trường hợp \(n = 1\) Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có: \(1 + 2 + 3 + ... + k = \frac{{k(k + 1)}}{2}\) Ta sẽ chứng minh mệnh đề cũng đúng với \(n = k + 1\), nghĩa là cần chứng minh \(1 + 2 + 3 + ... + k + (k + 1) = \frac{{(k + 1)(k + 2)}}{2}\) Thật vậy ta có \(\begin{array}{l}1 + 2 + 3 + ... + k + (k + 1) = \frac{{k(k + 1)}}{2} + (k + 1)\\ = \frac{{k(k + 1) + 2(k + 1)}}{2} = \frac{{(k + 1)(k + 2)}}{2}\end{array}\) Vậy mệnh đề đúng với mọi số tự nhiên \(n \ge 1\) Thực hành 2 Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên \(n \ge 3\) \({2^{n + 1}} > {n^2} + n + 2\) Phương pháp giải: Chứng minh mệnh đề đúng với \(n \ge p\) thì: Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\) Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận. Lời giải chi tiết: Ta chứng minh bằng quy nạp theo n. Bước 1: Với \(n = 3\) ta có \({2^{3 + 1}} > {3^2} + 3 + 2\) Như vậy mệnh đề đúng cho trường hợp \(n = 3\) Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có: \({2^{k + 1}} > {k^2} + k + 2\) Ta sẽ chứng minh bất đẳng thức đúng với \(n = k + 1\), nghĩa là cần chứng minh \({2^{k + 1 + 1}} > {(k + 1)^2} + k + 1 + 2\) Sử dụng giả thiết quy nạp, với lưu ý \(k \ge 3\), ta có \(\begin{array}{l}{2^{k + 1 + 1}} = {2.2^{k + 1}}\\\quad \quad > 2({k^2} + k + 2) = {(k + 1)^2} + {k^2} + 1 + 2\\\quad \quad > {(k + 1)^2} + k + 1 + 2\end{array}\) Vậy bất đẳng thức đúng với \(n = k + 1\). Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên \(n \ge 3\).
|














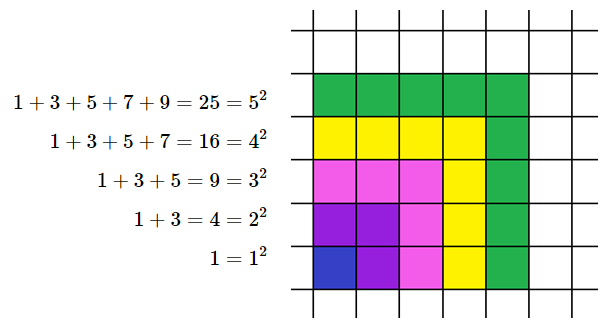






Danh sách bình luận