Đề kiểm tra 45 phút chương 3 phần Hình học 7 - Đề số 1

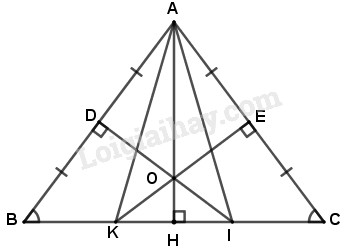
Đề bài

Câu 1. (2 điểm) Cho tam giác \(ABC\). Hãy điền vào chỗ trống trong các khẳng định dưới đây để được khẳng định đúng :

a) \(AB+AC\).....; \(AC+BC\).....; \(AB+BC\).....

b) \(AB-AC\).....; \(AC-BC\).....; \(AB-BC\).....

Câu 2. (1 điểm) Trong các khẳng định sau đây, khẳng định nào đúng ?

Trọng tâm của tam giác là:

(A) Giao điểm của ba đường cao của tam giác đó;

(B) Giao điểm của ba đường trung trực của tam giác đó;

(C) Giao điểm của ba đường trung tuyến của tam giác đó;

(D) Giao điểm của ba đường phân giác của tam giác đó.

Câu 3. (7 điểm) Cho tam giác \(ABC\) cân tại đỉnh \(A\); \(D\) và \(E\) lần lượt là trung điểm của \(AB\) và \(AC\). Các đường trung trực của \(AB,AC\) cắt nhau tại \(O\) và lần lượt cắt \(BC\) tại \(I\) và \(K\) (hình vẽ).

a) Các tam giác \(AIB\) và \(AKC\) là những tam giác g? Tại sao ? (2 điểm);

b) Chứng minh \(\Delta ADO=\Delta AEO\) (2 điểm);

c) Chứng minh \(O\) là trực tâm của cả hai tam giác \(AIB\) và \(AKC\) (3 điểm).

Lời giải chi tiết

Câu 1:

Phương pháp giải:

 Áp dụng kiến thức: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

Cách giải:

a) \(AB+AC\)\(>BC\); \(AC+BC\)\(>AB\); \(AB+BC\)\(>AC\).

b) \(AB-AC\)\(<BC\); \(AC-BC\)\(<AB\); \(AB-BC\)\(<AC\).

Câu 2:

Phương pháp giải:

 Vận dụng kiến thức về trọng tâm - điểm chung của ba đường trung tuyến trong một tam giác.

Cách giải:

Trọng tâm của tam giác là giao điểm của ba đường trung tuyến của tam giác đó.

Chọn C.

Câu 3:

Phương pháp giải:

- Áp dụng kiến thức về tính chất đường trung trực của một đoạn thẳng.

- Chứng minh hai tam giác bằng nhau theo các trường hợp bằng nhau của tam giác vuông.

- Chứng minh \(O\) là giao điểm của hai đường cao trong tam giác \(AIB\) và \(AKC\).

Cách giải: 

a) Xét \(\Delta AIB\) có \(I\) nằm trên đường trung trực của cạnh \(AB\) nên \(IA = IB.\)

Vậy tam giác \(AIB\) là tam giác cân tại \(I.\)

Chứng minh tương tự ta cũng có tam giác \(AKC\) cân tại \(K\).

b) Xét \(\Delta ADO\) và \(\Delta AEO\) có

\(\widehat D = \widehat E\left( { = 90^\circ } \right)\) (cách vẽ đường trung trực)

\(AO\) là cạnh chung

\(AD = AE = \dfrac{1}{2}AB = \dfrac{1}{2}AC\)

Vậy \(\Delta ADO = \Delta AEO\) (cạnh huyền – cạnh góc vuông).

c) \(\Delta ABC\) có \(O\) là giao điểm của hai đường trung trực của cạnh \(AB\) và \(AC\) nên đường thẳng đi qua \(A,O\) là đường trung trực của cạnh \(BC.\)

Gọi giao điểm của \(AO\) với \(BC\) là \(H.\)

Ta có \(\Delta ABC\) cân tại \(A\) nên \(AH\) đồng thời là đường trung trực và là đường cao của tam giác.

Xét \(AIB\) có :

\(AH \bot BI\)

\(ID \bot AB\)

\(AH \cap ID = \left\{ O \right\}\)

Vậy \(O\) là trực tâm của tam giác \(ABI\) (ba đường cao trong một tam giác đồng quy tại một điểm, điểm đó gọi là trực tâm). 

Chứng minh tương tự ta có \(O\) là trực tâm của \(\Delta AKC.\)

Loigiaihay.com