Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Đề bài

 

Tìm hai số không âm a và b có tổng bằng 10 sao cho:

 a) Biểu thức ab đạt giá trị lớn nhất;

b) Tổng bình phương của chúng đạt giá trị nhỏ nhất;

c) Biểu thức \(a{b^2}\) đạt giá trị lớn nhất

Lời giải chi tiết

Ta có: a, b > 0 và a + b = 10

a) Đặt: \(f(a) = ab = a(10 - a) =  - {a^2} + 10a\)

\(f'(a) =  - 2a + 10 = 0 \Leftrightarrow a = 5\)

Bảng biến thiên:

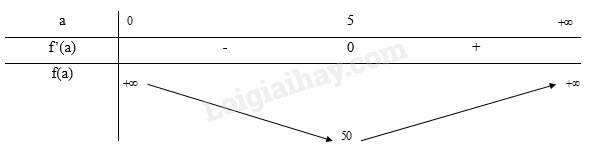
Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(5) = 25\)

Vậy để biểu thức ab đạt giá trị lớn nhất là 25 thì a = 5 và b = 5

b) Đặt: \(f(a) = {a^2} + {b^2} = {a^2} + {(10 - a)^2} = 2{a^2} - 20a + 100\)

\(f'(a) = 4a - 20 = 0 \Leftrightarrow a = 5\)

Bảng biến thiên:

Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_{(0; + \infty )} f(a) = f(5) = 50\)

Vậy để biểu thức \({a^2} + {b^2}\) đạt giá trị nhỏ nhất là 50 thì a = 5 và b = 5

c) Đặt: \(f(a) = a{b^2} = a{(10 - a)^2} = {a^3} - 20{a^2} + 100a\)

\(f'(a) = 3{a^2} - 40a + 100 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{10}}{3}\\a = 10\end{array} \right.\)

Bảng biến thiên:

Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(\frac{{10}}{3}) = \frac{{4000}}{{27}}\)

Vậy để biểu thức \(a{b^2}\) đạt giá trị lớn nhất là \(\frac{{4000}}{{27}}\) thì a = \(\frac{{10}}{3}\) và b = \(\frac{{20}}{3}\)