Giải bài tập 2 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạoXét tính đơn điệu và tìm điểm cực trị của các hàm số sau: a) (y = 4{x^3} + 3{x^2}--36x + 6) b) (y = frac{{{x^2} - 2x - 7}}{{x - 4}}) Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Đề bài
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: Phương pháp giải - Xem chi tiết Tìm tập xác định, đạo hàm và lập bảng biến thiên. Lời giải chi tiết a) \(y = 4{x^3} + 3{x^2}-36x + 6\) Tập xác định: \(D = \mathbb{R}\) \(y' = 12{x^2} + 6x - 36\) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2}\\x = - 2\end{array} \right.\) Bảng biến thiên:
Hàm số đồng biến trên khoảng (\( - \infty \);-2) và (\(\frac{3}{2}\);\( + \infty \)), nghịch biến trên khoảng (-2; \(\frac{3}{2}\)) Hàm số đạt cực đại tại x = -2, \({y_{cd}} = f( - 2) = 58\), đạt cực tiểu tại x = \(\frac{3}{2}\), \({y_{ct}} = f(\frac{3}{2}) = - \frac{{111}}{4}\) b) \(y = \frac{{{x^2} - 2x - 7}}{{x - 4}}\) Tập xác định: \(D = \mathbb{R}\backslash \{ 4\} \) \(y' = \frac{{{x^2} - 8x + 15}}{{{x^2} - 8x + 16}}\) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 3\end{array} \right.\) Bảng biến thiên:
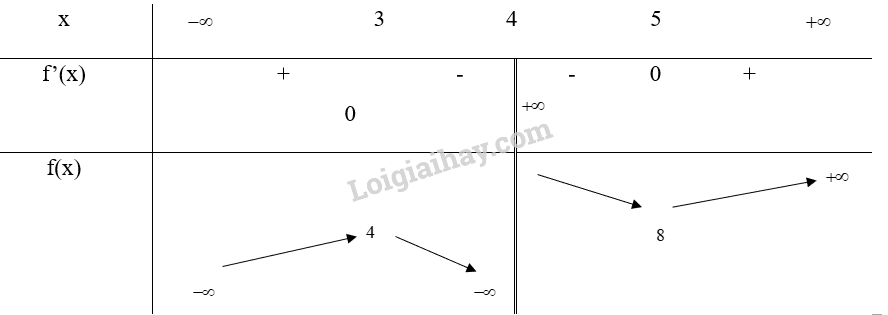
Hàm số đồng biến trên khoảng (\( - \infty \);3) và (5;\( + \infty \)), nghịch biến trên khoảng (3;4) và (4;5) Hàm số đạt cực đại tại x = 3, \({y_{cd}} = f(3) = 4\), đạt cực tiểu tại x = \(5\), \({y_{ct}} = f(5) = 8\)  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
