Bài 99 trang 122 SBT toán 9 tập 1

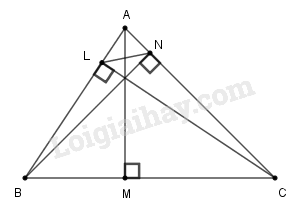
Đề bài

Gọi $AM, BN, CL$ là ba đường cao của tam giác $ABC$. Chứng minh:

a) $∆ANL$ đồng dạng $∆ABC$;

b) $AN.BL.CM$ $= AB.BC.CA.cosA.cosB.cosC.$

Lời giải chi tiết

a) Xét hai tam giác $BNA$ và $CLA$, ta có:

$\widehat {BNA} = \widehat {CLA} = 90^\circ$

$\widehat A$ chung

Suy ra $∆BNA$ đồng dạng $∆CLA$ (g.g)

Suy ra: $\displaystyle {{AL} \over {AN}} = {{AC} \over {AB}} \Rightarrow {{AL} \over {AC}} = {{AN} \over {AB}}$

Xét hai tam giác $ABC$ và $ANL$, ta có:

$\displaystyle {{AL} \over {AC}} = {{AN} \over {AB}}$

$\widehat A$ chung

Suy ra $∆ABC$ đồng dạng $∆ANL$ (c.g.c)

b) $ABN$ vuông tại $N$ nên $AN = AB.\cos \widehat B\,(1)$

$∆BCL$ vuông tại $L$ nên $BL = BC.\cos \widehat B\,(2)$

$∆ACM$ vuông tại $M$ nên $CM = AC.\cos \widehat C\,(3)$

Từ (1), (2) và (3) suy ra: 

$AN.BL.CM$$= AB.BC.CA.\cos \widehat A\cos \widehat B\cos \widehat C.$

Loigiaihay.com