Bài 9.2 phần bài tập bổ sung trang 111 SBT toán 9 tập 2Giải bài 9.2 phần bài tập bổ sung trang 111 sách bài tập toán 9. Tính chu vi của hình cánh hoa, biết OA = R... Quảng cáo
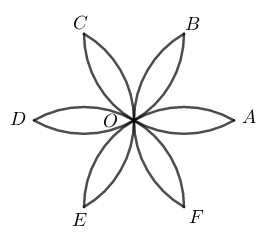
Đề bài Tính chu vi của hình cánh hoa, biết \(OA = R\) \((h.bs.6).\)
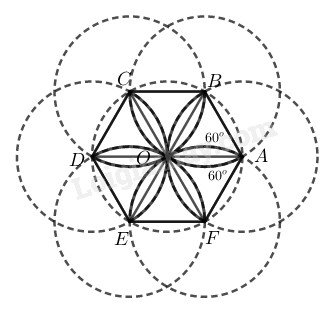
Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. +) Trong đường tròn \(R,\) độ dài \(l\) của một cung \(n^\circ\) được tính theo công thức: \(l=\dfrac{\pi Rn}{180}.\) Lời giải chi tiết Hình vẽ có \(6\) cung tròn bằng nhau có bán kính bằng \(R\) \(\overparen{BOF}\) của đường tròn \((A; R)\) \(\overparen{AOC}\) của đường tròn \((B; R)\) \(\overparen{BOD}\) của đường tròn \((C; R)\) \(\overparen{COE}\) của đường tròn \((D; R)\) \(\overparen{DOF}\) của đường tròn \((E; R)\) \(\overparen{EOA}\) của đường tròn \((F; R)\)
Vì ABCDEF là lục giác đều nội tiếp đường tròn tâm O (theo cách vẽ hình cánh hoa) nên \(AB = BC = CD = DE = EF\) Từ đó suy ra các tam giác OAB, OBC, OCD, ODE, OEF, OFA bằng nhau (c-c-c) Nên: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD}\)\( = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \dfrac{{{{360}^0}}}{6} = {60^0}\) Vì OA=OB và \(\widehat {AOB} =60^0\) nên \(∆AOB\) đều, tương tự ta có \(∆AOF\) đều nên \(\widehat {BAF} = {120^\circ}\) \( \Rightarrow sđ \overparen{BOF}=120^\circ\) \(l = \displaystyle {{\pi R.120} \over {180}} = {{2\pi R} \over 3}\) Chu vi cánh hoa: \(\displaystyle {{2\pi R} \over 3}.6 = 4\pi R\) Loigiaihay.com
|




















Danh sách bình luận