Bài 86 trang 120 SBT toán 9 tập 1

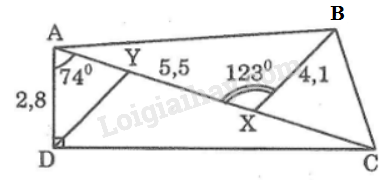
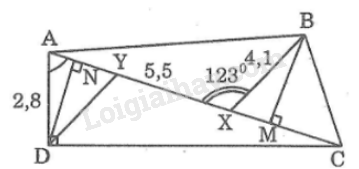
Đề bài

Cho hình 32. 

Biết:

\(AD \bot DC,\widehat {DAC} = 74^\circ \)

\(\widehat {AXB} = 123^\circ ,AD = 2,8\,cm\); \(AX = 5,5cm, BX = 4,1cm.\)

a) Tính \(AC\).

b) Gọi \(Y\) là điểm trên \(AX\) sao cho \(DY ⁄⁄ BX\). Hãy tính \(XY\)

c) Tính diện tích tam giác \(BCX\).

Lời giải chi tiết

a) Trong tam giác vuông ACD, ta có:

\(AC = \displaystyle {{AD} \over {\cos \widehat {CAD}}} = {{2,8} \over {\cos 74^\circ }}\)\( \approx 10,158\,(cm)\)

b) Kẻ \(DN \bot AC\)

Trong tam giác vuông \(AND\), ta có:

\(\eqalign{
& DN = AD.\sin \widehat {DAN} \cr 
& = 2,8.\sin 74^\circ \approx 2,692\,(cm) \cr} \)

\(\eqalign{
& AN = AD.\cos \widehat {DAN} \cr 
& = 2,8.\cos 74^\circ \approx 0,772\,(cm) \cr} \)

Vì \(BX // DY\) nên \(\widehat {D{\rm{YX}}} = \widehat {BXY} = 123^\circ \) ( hai góc so le trong)

Mà \(\widehat {DYN} + \widehat {D{\rm{YX}}} = 180^\circ \) (kề bù)

Suy ra:

\(\widehat {DYN} = 180^\circ  - \widehat {D{\rm{YX}}} = 180^\circ  - 123^\circ\)\(  = 57^\circ \)

Trong tam giác vuông \(DYN\), ta có:

\(\eqalign{
& NY = DN.\cot \widehat {DYN} \cr 
& \approx 2,692.\cot 57^\circ \approx 1,748\,(cm) \cr} \)

Ta có: 

\(\eqalign{
& XY = AX - (AN + NY) \cr 
& = 5,5 - (0,772 + 1,748) = 2,98cm \cr} \)

c) Ta có:

\(CX = AC - AX \approx 10,158 - 5,5\)\( = 4,658\,(cm)\)

Kẻ \(BM \bot CX\)

Ta có:

\(\widehat {BXC} = 180^\circ  - \widehat {BXA} = 180^\circ  - 123^\circ\)\(  = 57^\circ \)

Trong tam giác vuông BMX, ta có:

\(\eqalign{
& BM = BX.\sin \widehat {BXC} \cr 
& = 4,1.\sin 57^\circ \approx 3,439\,(cm) \cr} \)

\(\eqalign{
& {S_{BCX}} = {1 \over 2}BM.CX \cr 
& = {1 \over 2}.3,439.4,658 \approx 8,009\,\left( {c{m^2}} \right). \cr} \)

Loigiaihay.com