Bài 83* trang 171 SBT toán 9 tập 1

Đề bài

Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B,\) \(OO' = 3cm.\) Qua \(A\) kẻ một đường thẳng cắt các đường tròn \((O)\) và \((O')\) theo thứ tự tại \(E\) và \(F\) ( \(A\) nằm giữa \(E\) và \(F\)). Tính xem đoạn thẳng \(EF\) có độ dài lớn nhất bằng bao nhiêu\(?\) 

Lời giải chi tiết

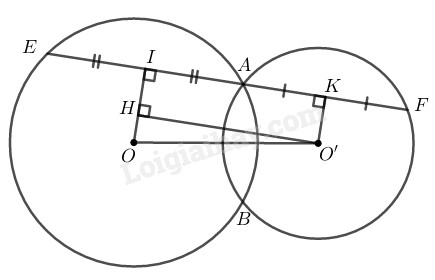
Kẻ \(OI ⊥ AE, O'K ⊥ AF\)

Trong đường tròn \((O),\) có \(OI ⊥ AE\) mà OI là 1 phần đường kính và AE là dây cung nên: 

\( IA = IE = \displaystyle {1 \over 2}AE\) ( đường kính vuông góc với dây cung)

Trong đường tròn \((O'),\) có \(O'K ⊥ AF\) mà O'K là 1 phần đường kính và AF là dây cung nên: 

\(KA = KF = \displaystyle {1 \over 2}AF\) (đường kính vuông góc với dây cung)

Ta có: \( EF = AE + AF\)

Suy ra: \(EF = 2IA + 2AK \)\(= 2(IA + AK) = 2IK    \; \;(1)\)

Kẻ \(O'H ⊥ OI\)

Khi đó tứ giác \(IHO'K\) là hình chữ nhật ( có ba góc vuông)

Suy ra: \(O'H = IK\)

Trong tam giác \(OHO'\) ta có: \(O’H  \le {\rm{OO'}}=3\; (cm)\)

Suy ra: \(IK  \le {\rm{OO}}'\)      \((2)\)

Từ \((1)\) và \((2)\) suy ra: \(EF  \le {\rm{2OO'}}= 6 (cm)\)

Ta có: \(EF = 6cm\) khi \(H\) và \(O\) trùng nhau hay \(EF // OO'\)

Vậy \(EF\) có độ dài lớn nhất bằng \(6cm\) khi và chỉ khi \(EF // OO'.\)

Loigiaihay.com