Bài 77 trang 118 SBT toán 9 tập 1

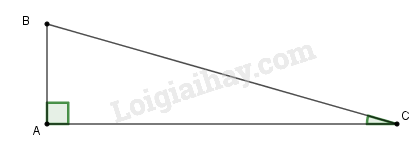
Đề bài

Bài toán máy bay hạ cánh  

Một máy bay đang bay ở độ cao \(10km\). Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu phi công muốn tạo góc nghiêng \(3^\circ \) thì cách sân bay bao nhiêu ki-lô-mét phải bắt đầu cho máy bay hạ cánh ?

b) Nếu cách sân bay \(300km\) máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu? 

Lời giải chi tiết

a) Ta có hình vẽ: Độ cao máy bay là \(AB=10km\), góc nghiêng \(\widehat C=3^0\). Ta tính BC. 

 

Vậy khoảng cách từ máy bay đến sân bay là:

\(BC=\dfrac{{AB}}{{\sin \widehat C}}\)\(=\displaystyle {{10} \over {\sin 3^\circ }} \approx 191\;(km)\)

b) Ta có hình vẽ: Khi đó \(AB=10km, BC=300km\) 

Gọi \(\widehat C=\beta\) là góc nghiêng của đường đi máy bay so với mặt đất. 

Ta có : \(\displaystyle \sin \beta  =\dfrac{AB}{BC}\)\(= \displaystyle {{10} \over {300}} = {1 \over {30}}\).

Suy ra: \(\beta  \approx 1^\circ 55'\).

Nếu cách sân bay \(300km\) máy bay bắt đầu hạ cánh thì góc nghiêng là \(1^\circ 55'\).

Loigiaihay.com