Giải bài 7 trang 34 sách bài tập toán 12 - Chân trời sáng tạoĐồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 3. Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng A. \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;2} \right)\). B. \(\left( { - 2;0} \right)\). C. \(\left( { - 4; - 3} \right)\) và \(\left( { - 1;2} \right)\). D. \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\). Quảng cáo
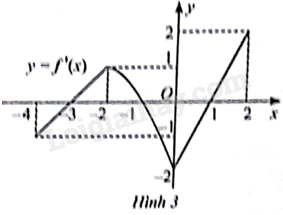
Đề bài Đồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 3. Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng A. \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;2} \right)\). B. \(\left( { - 2;0} \right)\). C. \(\left( { - 4; - 3} \right)\) và \(\left( { - 1;2} \right)\). D. \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\).
Phương pháp giải - Xem chi tiết Từ đồ thị hàm số \(y = f'\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\) rồi xác định tính đồng biến, nghịch biến của hàm số. Lời giải chi tiết Ta có: \(y' = 0\) khi \(x = - 1;x = - 3\) hoặc \(x = 1\). Bảng xét dấu đạo hàm của hàm số:
Dựa vào bảng xét dấu đạo hàm ta có: Hàm số đồng biến trên các khoảng \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\). Chọn D.
|





















Danh sách bình luận