Bài 67 trang 63 SBT toán 9 tập 2

LG a

Vẽ đồ thị của hai hàm số này trong cùng một mặt phẳng tọa độ.

Phương pháp giải:

Xác định các điểm thuộc đồ thị rồi vẽ đồ thị hàm số.

Lời giải chi tiết:

Vẽ đồ thị hàm số: \(y = 2x - 3\)

Cho \(x = 0 ⇒ y = -3\) ta được điểm \((0; -3)\)

Cho \(y = 0 ⇒ x = 1,5\) ta được điểm \((1,5; 0)\)

Đường thẳng đi qua hai điểm có tọa độ \((0; -3)\) và \((1,5; 0)\) là đồ thị hàm số \(y = 2x - 3\)

Vẽ đồ thị hàm số \(y=-x^2\):

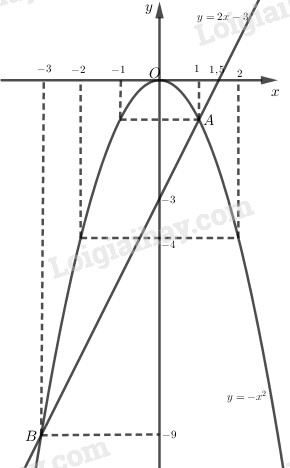
Đồ thị:

LG b

Tìm tọa độ các giao điểm của hai đồ thị.

Phương pháp giải:

Dựa vào đồ thị hàm số để suy ra giao điểm

Lời giải chi tiết:

Từ đồ thị ta thấy tọa độ giao điểm của hai đồ thị: \(A(1; -1)\) và \(B(-3; -9)\)

LG c

Kiểm nghiệm rằng tọa độ của mỗi giao điểm đều là nghiệm chung của hai phương trình hai ẩn \(y = 2x – 3 \) và \(y =  - {x^2}\)

Phương pháp giải:

Thay tọa độ giao điểm vào mỗi phương trình để suy ra nghiệm.

Lời giải chi tiết:

Thay tọa độ của \(A\) và \(B\) vào phương trình: \(y = 2x - 3\) ta có:

\( - 1 = 2.1 - 3\Leftrightarrow -1=-1\) (luôn đúng)

\( - 9 = 2.\left( { - 3} \right) - 3 \Leftrightarrow -9=-9\) (luôn đúng)

Thay tọa độ của \(A\) và \(B\) vào phương trình: \(y =  - {x^2}\)

\( - 1 =  - {1^2} \Leftrightarrow -1=  - 1\) (luôn đúng)

\(- 9 =  - {\left( { - 3} \right)^2} \Leftrightarrow -9=  - 9\) (luôn đúng)

Vậy tọa độ của \(A\) và \(B\) là nghiệm của hệ phương trình:  

\(\left\{ {\matrix{
{y = 2x - 3} \cr 
{y = - {x^2}} \cr} } \right.\)

Loigiaihay.com