Bài 6.3 phần bài tập bổ sung trang 106 SBT toán 9 tập 2

Đề bài

Cho tam giác \(ABC\) có ba góc nhọn. Xác định vị trí của điểm \(M\) trong tam giác sao cho \(MA + MB + MC\) nhỏ nhất.

Lời giải chi tiết

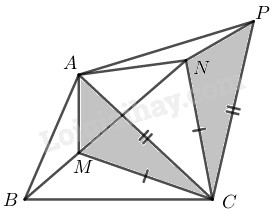
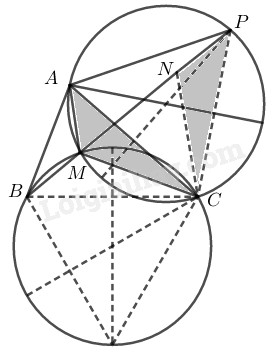
Trong \(∆ABC\) ta lấy điểm \(M.\) Nối \(MA, MB, MC.\)

Ta cần làm xuất hiện tổng \(MA + MB + MC\) sau đó tìm điều kiện để tổng đó nhỏ nhất.

Lấy \(MC\) làm cạnh dựng trên nửa mặt phẳng bờ \(BC\) chứa điểm \(A\) tam giác đều \(MCN.\) Suy ra: \(CM = MN.\)

Lấy \(AC\) làm cạnh dựng trên nửa mặt phẳng bờ \(AC\) không chứa điểm \(B\) tam giác đều \(APC.\)

Ta có:

\(\widehat {MCA} + \widehat {ACN} = \widehat {MCN}=60^\circ \)

\(\widehat {ACN} + \widehat {NCP} =\widehat {ACP}= 60^\circ \)

\( \Rightarrow \widehat {MCA} = \widehat {NCP}\) 

Xét \(∆AMC\) và \(∆PNC:\)

+) \(CM = CN\) (vì \(∆MCN\) đều)

+) \(\widehat {MCA} = \widehat {NCP}\) (chứng minh trên)

+) \( CA = CP\) (vì \(∆APC\) đều)

Suy ra: \(∆AMC = ∆PNC\;\; (c.g.c)\)

\( \Rightarrow         PN = AM\)

\( MA + MB + MC = NP + MB + MN\)

Ta có \(∆ABC\) cho trước nên điểm \(P\) cố định nên \(BM + MN + NP\) ngắn nhất khi \(4\) điểm \(B, M, N, P\) thẳng hàng.

Vì \(\widehat {CMN} = 60^\circ \) nên \(3\) điểm \(B, M, N\) thẳng hàng khi và chỉ khi \(\widehat {BMC} = 120^\circ \)

Vì \(\widehat {CNM} = 60^\circ \) nên \(3\) điểm \(M, N, P\) thẳng hàng khi và chỉ khi \(\widehat {CNP} = 120^\circ \)

Mà \(∆AMC = ∆PNC\) (chứng minh trên)     \( \Rightarrow \widehat {AMC} = \widehat {PNC} = 120^\circ \)

Vậy \(MA + MB + MC\) bé nhất khi và chỉ khi \(\widehat {BMC} = 120^\circ \)  và \(\widehat {AMC} = 120^\circ \)

Vậy \(M\) là giao điểm của \(2\) cung chứa góc \(120^\circ \) dựng trên \(BC\)  và \(AC.\)

Loigiaihay.com