Bài 62 trang 102 Vở bài tập toán 7 tập 2

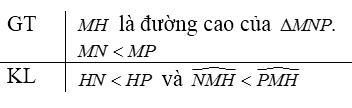
Đề bài

Gọi \(MH\) là đường cao của tam giác \(MNP.\) Chứng minh rằng: Nếu \(MN < MP\) thì \(HN < HP\)  và  \(\widehat {NMH} < \widehat {PMH}\) (yêu cầu xét hai trường hợp: khi góc \(N\) nhọn và khi góc \(N\) tù).

Lời giải chi tiết

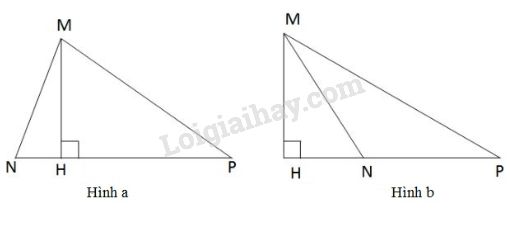
- Khi góc \(N\) nhọn (hình a) : \(H\) nằm giữa \(N\) và \(P.\) Hình chiếu của \(MN\) và \(MP\) lần lượt là \(HN\) và \(HP.\) 

Theo giả thiết \(MN < MP\) suy ra \( HN < HP\) (quan hệ giữa các đường xiên và hình chiếu).

Trong tam giác \(MNP\), do \(MN < MP\) nên \(\widehat {MPN} < \widehat {MNP}\) (1) (quan hệ giữa góc và cạnh đối diện trong tam giác)    

Mặt khác trong các tam giác vuông \(MHN\) và \(MHP\), ta có

  \(\widehat {NMH} + \widehat {MNH} \)\(=\widehat {MPH} + \widehat {PMH} = {90^o}\)   (2)

Từ (1) và (2) suy ra  \(\widehat {NMH} < \widehat {PMH}\)

- Khi góc \(N\) tù (hình b) : \(H\) nằm trên tia đối của tia \(NP\) hay điểm \(N\) ở giữa \(H\) và \(P\)

Từ \(MN<MP\), lập luận tương tự như trên ta suy ra \( HN < HP.\)

Do điểm \(N\) nằm giữa \(H\) và \(P\) nên tia \(MN\) nằm giữa hai tia \(MH\) và \(MP.\)

Từ đó suy ra  \(\widehat {HMN} < \widehat {HMP}\).

Loigiaihay.com