Bài 53 trang 109 SBT toán 9 tập 2

Đề bài

Tính độ dài đường tròn ngoại tiếp:

\(a)\) Một lục giác đều có cạnh là \(4cm;\)

\(b)\) Một hình vuông có cạnh là \(4cm;\)

\(c)\) Một tam giác đều có cạnh là \(6cm.\)

Lời giải chi tiết

\(a)\) 

 

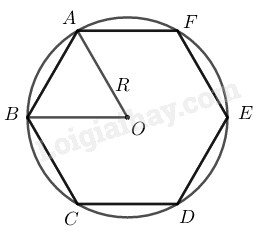
Cạnh lục giác đều nội tiếp trong đường tròn \((O; R)\) bằng bán kính \(R.\) Vì cạnh lục giác đều là \(4cm\) \( \Rightarrow R = 4 cm.\)

\(C = 2πR = 2. π. 4 = 8π (cm)\)

\(b)\)

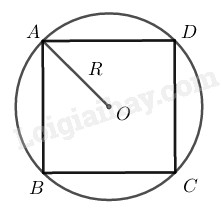
Đường tròn ngoại tiếp hình vuông có đường kính là đường chéo của hình vuông.

Độ dài đường chéo hình vuông có cạnh bằng \(4 (cm)\) là \(AC=\sqrt {AB^2+BC^2}=4\sqrt 2 \)\( (cm)\) (định lý Pytago)

Bán kính của đường tròn ngoại tiếp hình vuông:

\(R = \displaystyle {{4\sqrt 2 } \over 2} = 2\sqrt 2 \)

\(C = 2πR= 2. π. 2\sqrt 2 = 4π\sqrt 2  \;(cm)\) 

\(c)\)

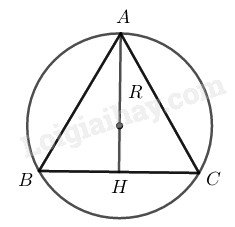
Vì tam giác đều nên giao điểm \(3\) đường trung trực cũng là giao điểm \(3\) đường cao, \(3\) đường trung tuyến nên bán kính của đường tròn ngoại tiếp bằng \(\displaystyle {2 \over 3}\) đường cao của tam giác đều.

Xét tam giác vuông \(AHB,\) ta có: 

\(AH = AB.\sin \widehat B = {\rm{6}}.\sin {\rm{6}}{0^\circ} \)\(=  \displaystyle {\rm{6}}.{{\sqrt 3 } \over 2} = 3\sqrt 3 \)

Bán kính \(R = \displaystyle  {2 \over 3}AH = {2 \over 3}.3\sqrt 3  = 2\sqrt 3 \)\( \;\;(cm)\)

\(C = 2πR = 2π.2\sqrt 3   = 4\sqrt 3 π  \;\;(cm).\)

Loigiaihay.com