Bài 5.2 phần bài tập bổ sung trang 105 SBT toán 9 tập 2

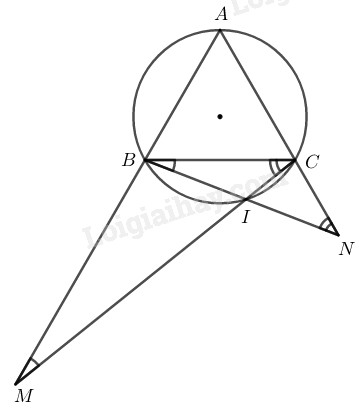
Đề bài

Cho đường tròn tâm \(O\) bán kính \(R.\) Lấy \(3\) điểm \(A, B, C\) trên đường tròn đó sao cho \(AB = BC = CA.\) Gọi \(I\) là điểm bất kỳ của cung nhỏ \(BC\) \((\)và \(I\) không trùng với \(B, C).\) Gọi \(M\) là giao điểm của \(CI\) và \(AB.\) Gọi \(N\) là giao điểm của \(BI\) và \(AC.\) Chứng minh:

\(a)\) \(\widehat {ANB} = \widehat {BCI}\)

\(b)\) \(\widehat {AMC} = \widehat {CBI}\)

Lời giải chi tiết

Vì \(AB = AC = BC\;\; (gt)\)

Suy ra các cung nhỏ \(\overparen{AB} = \overparen{AC} = \overparen{BC}\)   \((1)\)

\(a)\) Xét đường tròn \((O)\) có: \(\widehat {BCI} = \displaystyle {1 \over 2} sđ \overparen{BI}\) (tính chất góc nội tiếp)

hay \(\widehat {BCI} = \displaystyle{1 \over 2} (sđ \overparen{BC}- sđ \overparen{CI}\)) \( (2)\)

Từ \((1)\) và \((2)\) suy ra: \(\widehat {BCI} =\displaystyle {1 \over 2} (sđ \overparen{AB}- sđ \overparen{CI})\)    \(  (3)\)

Lại có: \(\widehat {ANB} = \displaystyle {1 \over 2} (sđ \overparen{AB}- sđ \overparen{CI})\) (góc có ở đỉnh bên ngoài đường tròn) \( (4)\)

Từ \((3)\) và \((4)\) suy ra: \(\widehat {ANB} = \widehat {BCI}\)

\(b)\) Xét đường tròn \((O)\) có:  \(\widehat {CBI} =\displaystyle {1 \over 2} sđ \overparen{CI}\) (tính chất góc nội tiếp)

Hay \(\widehat {CBI} = \displaystyle{1 \over 2} (sđ \overparen{BC}- sđ \overparen{BI}\)) \( (5)\)

Từ \((1)\) và \((5)\) suy ra: \(\widehat {CBI} = \displaystyle{1 \over 2} (sđ \overparen{AC}- sđ \overparen{BI}\)) \((6)\)

Lại có: \(\widehat {AMC} = \displaystyle{1 \over 2} (sđ \overparen{AC}- sđ \overparen{BI}\)) (góc có đỉnh bên ngoài đường tròn) \((7)\)

Từ \((6)\) và \((7)\) suy ra: \(\widehat {AMC} = \widehat {CBI}\).

Loigiaihay.com