Bài 4.8 phần bài tâp bổ sung trang 117 SBT toán 9 Tập 1

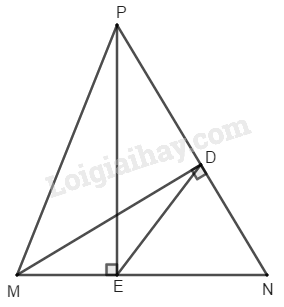
Đề bài

Cho tam giác nhọn \(MNP.\) Gọi \(D\) là chân đường cao của tam giác đó kẻ từ \(M.\) Chứng minh rằng:

a) \({S_{MNP}} = \dfrac{1}{2}MP.NP.\sin P;\)

b) \(DP = \dfrac{MN.sinN}{tan P};\)

c) \(∆DNE\) \(\backsim\) \(∆MNP,\) trong đó \(E\) là chân đường cao của tam giác \(MNP\) kẻ từ \(P.\)

Lời giải chi tiết

a) Xét tam giác MDP vuông tại D, ta có: \(MD = MP.sin\, P,\) suy ra: 

\({S_{MNP}} = \dfrac{1}{2}NP.MD \) \(= \dfrac{1}{2}NP.MP\sin P.\)

b) Xét tam giác MDN vuông tại D, ta có: \(MD = MN.sin \,N\)

Xét tam giác MDP vuông tại D, ta có: \(MD = DP.tan \,P\)

Suy ra \(DP=\dfrac{{MD}}{{\tan P}}=\dfrac{MN.sin N}{tan P}\)

c) Xét \(\Delta DMN\) và \(\Delta EPN\) có:

\(\widehat D = \widehat E\,( = 9{0^0})\)

\(\widehat N\) chung

Vậy \(\Delta DMN\) \(\backsim\) \(\Delta EPN\) (g-g)

\( \Rightarrow \dfrac{{DN}}{{MN}} = \dfrac{{EN}}{{PN}}\)

Xét \(\Delta DNE\) và \(\Delta MNP\) có:

\(\widehat N\) chung

\(\dfrac{{DN}}{{MN}} = \dfrac{{EN}}{{PN}}\)

Vậy \(\Delta DNE\) \(\backsim\) \(\Delta MNP\) (c-g-c).

Loigiaihay.com