Bài 4.5 phần bài tập bổ sung trang 117 SBT toán 9 Tập 1

Đề bài

Hãy tìm diện tích của tam giác cân có góc ở đáy bằng \(α\) nếu biết:

a) Cạnh bên bằng \(b ;\)                        

b) Cạnh đáy bằng \(a.\)

Lời giải chi tiết

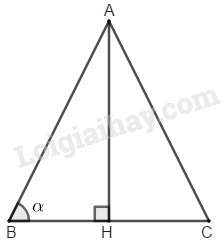
Xét tam giác cân \(ABC\) có \(AB = AC,\) \(\widehat {ABC} = \alpha, \) đường cao \(AH\)

a) \(AB = AC = b\)

Xét tam giác ABH vuông tại H ta có:

\(AH =AB.\sinα= b.\sinα,\) \( BH =AB.\cos α= b.cosα\) nên diện tích tam giác \(ABC\) là 

\(\eqalign{
& S = {1 \over 2}AH.BC = AH.BH \cr 
& = {b^2}\sin \alpha \cos \alpha . \cr} \)

b) \(BC = a\) 

Vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến. Suy ra \(BH = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Xét tam giác ABH vuông tại H, ta có: \(AH =BH.\tan \alpha = \eqalign{a \over 2}tan\alpha \)

nên diện tích tam giác \(ABC\) là: \(S = \eqalign{1 \over 2}.BC.AH\)\(=\dfrac{a}{2}.\dfrac{a}{2}\tan \alpha  = \eqalign{{{a^2}} \over 4}tan\alpha \).

Loigiaihay.com