Bài 46 trang 163 SBT toán 9 tập 1Giải bài 46 trang 163 sách bài tập toán 9. Cho góc nhọn xOy, điểm A thuộc tia Ox. Dựng đường tròn tâm I tiếp xúc với Ox tại A và có tâm I nằm trên tia Oy. Quảng cáo
Đề bài Cho góc nhọn \(xOy,\) điểm \(A\) thuộc tia \(Ox.\) Dựng đường tròn tâm \(I\) tiếp xúc với \(Ox\) tại \(A\) và có tâm \(I\) nằm trên tia \(Oy.\) Phương pháp giải - Xem chi tiết * Phân tích: +) Giả sử đã có một hình thỏa mãn điều kiện bài toán +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...) +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.) * Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ. * Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra. * Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài Lời giải chi tiết
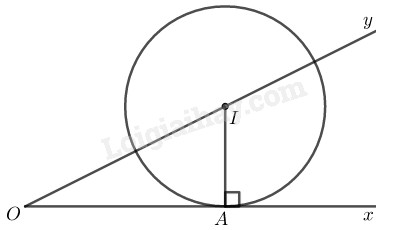
* Phân tích Giả sử đường tròn tâm \(I\) dựng được thỏa mãn điều kiện bài toán. − Đường tròn tâm \(I\) tiếp xúc với \(Ox\) tại \(A\) nên \(I\) nằm trên đường thẳng vuông góc với \(Ox\) kẻ từ \(A.\) − Tâm \(I\) nằm trên tia \(Oy\) nên \(I\) là giao điểm của \(Oy\) và đường thẳng vuông góc với \(Ox\) tại \(A.\) * Cách dựng − Dựng đường vuông góc với \(Ox\) tại \(A\) cắt \(Oy\) tại \(I.\) − Vẽ đường tròn \((I; IA)\) là đường tròn cần dựng. * Chứng minh Ta có: \(I\) thuộc \(Oy,\)\( OA ⊥ IA\) tại \(A.\) Suy ra \(Ox\) là tiếp tuyến của đường tròn \(( I;IA)\) hay \((I; IA)\) tiếp xúc với \(Ox.\) * Biện luận Vì \(\widehat {xOy}\) là góc nhọn nên đường thẳng vuông góc với \(Ox\) tại \(A\) luôn cắt tia \(Oy\) nên tâm \(I\) luôn xác định và duy nhất. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
