Bài 39 trang 162 SBT toán 9 tập 1

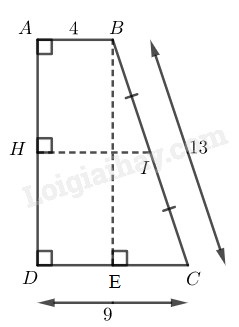
Đề bài

Cho hình thang vuông \(ABCD\) \((\widehat A = \widehat D = 90^\circ ),\) \(AB = 4cm,\) \(BC = 13cm,\) \(CD = 9cm.\)

\(a)\) Tính độ dài \(AD.\) 

\(b)\) Chứng minh rằng đường thẳng \(AD\) tiếp xúc với đường tròn có đường kính là \(BC.\)

Lời giải chi tiết

\(a)\) Kẻ \(BE ⊥ CD\) tại \(E\)

Suy ra tứ giác \(ABED\) là hình hình chữ nhật (vì có ba góc vuông \(\widehat A = \widehat D = \widehat E = {90^0}\))

Suy ra \(AD = BE\), \(DE = AB = 4 (cm)\)

Suy ra: \(CE = CD – DE = 9 – 4 = 5 (cm)\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(BCE\) ta có:

\(B{C^2} = B{E^2} + C{E^2}\)

Suy ra: \(B{E^2} = B{C^2} - C{E^2} \)\(= {13^2} - {5^2} = 144\)

             \(BE = 12 (cm)\)

 Vậy:  \(AD = 12 (cm)\)

\(b)\) Gọi \(I\) là trung điểm của \(BC\)

Ta có: \(IB = IC = \displaystyle {1 \over 2}BC \)\(= \displaystyle {1 \over 2}.13 = 6,5 (cm)\)  \((1)\)

Kẻ \(IH ⊥ AD.\)

Xét hình thang ABCD ta có: \(IH//AB//CD\) (cùng vuông góc với AD), mà I là trung điểm BC nên H là trung điểm AD.

Khi đó \(HI\) là đường trung bình của hình thang \(ABCD.\)

Ta có: \(HI = \displaystyle {{AB + CD} \over 2} \)\(= \displaystyle {{4 + 9} \over 2} = 6,5 (cm)\)  \((2)\)

Từ \((1)\) và \((2)\) suy ra: \(IH=IB=\displaystyle {1 \over 2}BC \)

Vậy đường tròn \(\left( {I;\displaystyle {{BC} \over 2}} \right)\) tiếp xúc với đường thẳng \(AD.\)

Loigiaihay.com