Bài 3.9 phần bài tập bổ sung trang 116 SBT toán 9 tập 2Giải bài 3.9 phần bài tập bổ sung trang 116 sách bài tập toán 9. Cho hình sau. Khi đó, số đo của... Quảng cáo
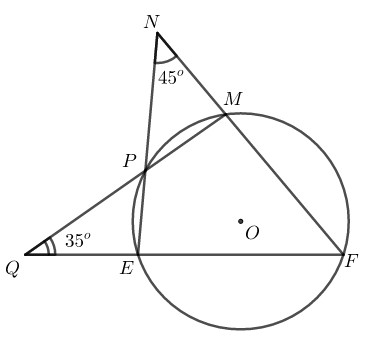
Đề bài Cho hình sau. Khi đó, số đo của \(\widehat {MFE}\) bằng bao nhiêu\(?\) \((A)\) \(50^\circ;\) \((B)\) \(80^\circ;\) \((C)\) \(130^\circ;\) \( (D)\) Không tính được.
Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn. +) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\) +) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn. +) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung. Lời giải chi tiết Xé đường tròn \((O),\) ta có: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\) (góc nội tiếp) \(=\dfrac{1}{2}(sđ \overparen{PM} +sđ \overparen{PE})\) Ta có: +) \(\widehat{N}=\dfrac{1}{2}(sđ \overparen{EF} -sđ \overparen{PM})\) (góc có đỉnh bên ngoài đường tròn) \(\Rightarrow sđ \overparen{EF}=2\widehat{N}+ sđ \overparen{PM}\) +) \(\widehat{Q}=\dfrac{1}{2}(sđ \overparen{MF} -sđ \overparen{PE})\) (góc có đỉnh bên ngoài đường tròn) \(\Rightarrow sđ \overparen{MF}=2 \widehat{Q}+sđ \overparen{PE}\) \(\Rightarrow sđ \overparen{MF}+sđ\overparen{EF}\)\(=2 (\widehat{Q}+\widehat{N})+(sđ \overparen{PE}+sđ \overparen{PM})\) \(\Rightarrow sđ \overparen{ME}(lớn)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\) Mà \(sđ \overparen{ME}(lớn)=360^\circ-sđ \overparen{ME}(nhỏ)\) \(\Rightarrow 360^\circ-sđ \overparen{ME}(nhỏ)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\) \(\Rightarrow sđ \overparen{ME}(nhỏ) =180^\circ-(\widehat{Q}+\widehat{N})\)\(=180^\circ-(35^\circ+45^\circ)=100^\circ\) Do đó: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\)\(= \dfrac{1}{2}.100^\circ=50^\circ\) Vậy chọn \((A)\) \(50^\circ\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
