Bài 37 trang 71 SBT toán 9 tập 1Giải bài 37 trang 71 sách bài tập toán 9. Cho các điểm M(-1 ; -2) , N(-2; -4), P(2; -3) , Q(3; -4,5). Tìm tọa độ của các điểm M’, N’, P’, Q’ lần lượt đồi xứng với các điểm M,N,P,Q qua trục Ox... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
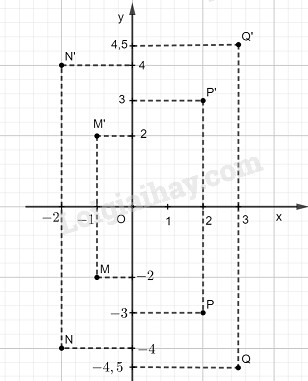
LG a Cho các điểm \(M(-1 ; -2)\), \(N(-2; -4)\), \(P(2; -3)\), \(Q(3; -4,5)\). Tìm tọa độ của các điểm \(M’, N’, P’, Q’\) lần lượt đồi xứng với các điểm \(M, N, P, Q\) qua trục \(Ox.\) Phương pháp giải: Điểm \(M(a;b)\) có điểm đối xứng qua trục Ox là \(N(a;-b)\) Lời giải chi tiết: Hình a Tọa độ các điểm \(M’, N’, P’ , Q’\) lần lượt đối xứng với các điểm \(M , N, P, Q\) qua trục \(Ox\): \(M'\left( {-1 ;2} \right),N'\left( { - 2;4} \right),\)\(P'\left( {2;3} \right),Q'\left( {3;4,5} \right)\) LG b Vẽ đồ thị của các hàm số sau trên cùng hệ trục tọa độ: \(\eqalign{ Phương pháp giải: * Để vẽ đồ thị \(y = \left| {f(x)} \right|\) Ta có: \(y = \left| f(x) \right| = \left\{ \matrix{ Vẽ đồ thị \( y= f(x)\) với \(f(x) \ge 0\) (1) Vẽ đồ thị \( y= - f(x)\) với \(f(x)<0\) (2) Đồ thị \(y = \left| {f(x)} \right|\) là hợp của hai đồ thị (1) và (2). Lời giải chi tiết: Hình b
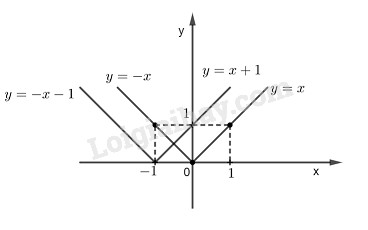
*Ta có: \(y = \left| x \right| = \left\{ \matrix{ Đồ thị hàm số \(y = x\) đi qua gốc tọa độ O và điểm \((1;1)\) Đồ thị hàm số \(y = -x\) đi qua gốc tọa độ O và điểm \((-1;1)\) Ta lấy phần nằm trên Ox của đồ thị hàm số \(y = x\) và phần nằm trên Ox của đồ thị hàm số \(y = -x\) ta được đồ thị hàm số \(y = \left| x \right|\) * Ta có : \(y = \left| {x + 1} \right| \)\(= \left\{ \matrix{ - Vẽ đồ thị hàm số \(y = x + 1\) Cho \(x = 0\) thì \(y = 1.\) Ta có: \((0;1)\) Cho \(y = 0\) thì \(x = -1.\) Ta có: \((-1;0)\) Đồ thị hàm số \(y = x + 1\) đi qua hai điểm \((0;1)\) và \((-1;0)\) - Vẽ đồ thị hàm số \(y = - (x + 1)\) Cho \(x = 0\) thì \(y = -1.\) Ta có : \((0;-1)\) Cho \(y = 0\) thì \(x = -1.\) Ta có : \((-1;0)\) Đồ thị hàm số \(y = - (x + 1)\) đi qua hai điểm \((0;-1)\) và \((-1;0)\) Ta lấy phần nằm trên Ox của các đồ thị hàm số \(y = x+1\) và \(y = -(x+1)\) ta được đồ thị hàm số \(y = \left| x+1 \right|\) nằm trên Ox LG c Tìm tọa độ giao điểm của đồ thị của các hàm số \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\). Từ đó , suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất. Phương pháp giải: Xét phương trình hoành độ giao điểm để tìm hoành tọa độ giao điểm hai đồ thị hàm số. Từ đó ta tìm được tung độ giao điểm. Lời giải chi tiết: Ta có : \(y = x\) và \(y = x + 1\) song song với nhau \(y = -x\) và \(y = -(x + 1)\) song song với nhau Suy ra chỉ có đồ thị hàm số \(y = -x\) và \(y = x + 1\) cắt nhau Phương trình hoành độ giao điểm: \( - x = x + 1 \Leftrightarrow 2x = - 1 \Leftrightarrow x = - \dfrac{1}{2}\) Suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất. Tung độ giao điểm: \(y = - x \Rightarrow y = \dfrac{1}{2}\) Vậy tọa độ giao điểm của đường thẳng \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\) là : \(I\left( { - \dfrac{1}{2};\dfrac{1 }{2}} \right)\) Loigiaihay.com
|




















Danh sách bình luận