Bài 27 trang 128 Vở bài tập toán 7 tập 1

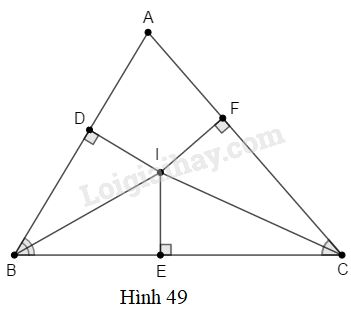
Đề bài

Cho tam giác \(ABC\), các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I\). Vẽ \(ID\) \(\perp\) \(AB\) (\(D\in AB\)), \(IE\) \(\perp\) \(BC\) (\(E\in BC\) ), \(IF\bot AC\) (\(F\in AC\))

CMR: \(ID=IE=IF\).

Lời giải chi tiết

Xét tam giác vuông \(BID\)  và \(BIE\) có:

cạnh huyền \(BI\) chung

góc nhọn \(\widehat{DBI}=\widehat{EBI}\) ( vì \(BI\) là tia phân giác góc \(B\))

Do đó \( ∆BID=∆BIE\)  (cạnh huyền - góc nhọn)

Suy ra \( ID=IE\) (cạnh tương ứng)        (1)

Xét hai tam giác vuông \(CIF\) và \(CIE\) có:

+) \(CI\) chung

+) \(\widehat{ICF}=\widehat{ICE}\) ( vì \(CI\) là phân giác góc \(C\))

\( \Rightarrow ∆CIF=∆CIE\) (cạnh huyền - góc nhọn).

Suy ra \(IE =IF\) (cạnh tương ứng)      (2)

Từ (1) và (2) suy ra \(ID=IE=IF\).

Loigiaihay.com