Bài 2.64 trang 105 SBT hình học 10

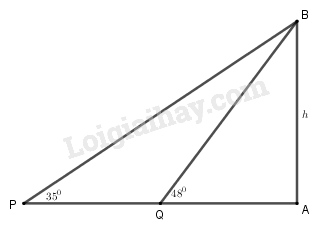
Đề bài

Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = {35^o}\)và \(\widehat {BQA} = {48^o}\).

a) Tính \(BQ\);

b) Tính chiều cao của tháp

Lời giải chi tiết

Ta có: \(\widehat {PBQ} = {48^ \circ } - {35^ \circ } = {13^ \circ }\).

Trong tam giác BPQ ta có: \(\dfrac{{BQ}}{{\sin P}} = \dfrac{{PQ}}{{\sin B}}\)\( \Leftrightarrow \dfrac{{BQ}}{{\sin {{35}^ \circ }}} = \dfrac{{300}}{{\sin {{13}^ \circ }}}\)

Do đó: \(BQ = \dfrac{{300.\sin {{35}^ \circ }}}{{\sin {{13}^ \circ }}} \approx 764,935(m)\)

b) Chiều cao của tháp là \(AB = BQ\sin {48^ \circ }\)\( \approx 764,935.\sin {48^ \circ } \approx 568,457(m)\)

Loigiaihay.com