Bài 22 trang 204 SBT Hình học 10

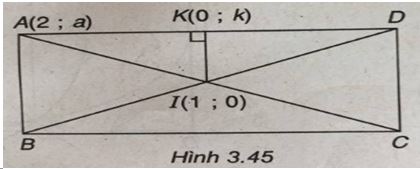
Đề bài

Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có \({x_A} = 2\) , điểm C và trung điểm K của AD cùng thuộc trục Oy, tâm I thuộc trục Ox, AD = 2AB. Tìm tọa độ các đỉnh của hình chữ nhật ABCD, biết rằng K có tung độ âm.

Lời giải chi tiết

Đặt A(2 ; a); K(0 ; k); C(0 ; c); I(1 ; 0) là tọa độ các điểm đã cho ta có

\(\frac{{a + c}}{2} = 0 \Rightarrow c =  - a.\)

\(AD = 2AB \Rightarrow AK = 2KI.\)

Ta có : \(\overrightarrow {AK}  = ( - 2;k - 1),\,\overrightarrow {IK}  = ( - 1;k)\)

\(\left\{ \begin{array}{l}\overrightarrow {AK} .\overrightarrow {IK}  = o\\\left| {\overrightarrow {AK} } \right| = 2\left| {\overrightarrow {IK} } \right|\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}2 + k(k - a) = 0\\{\overrightarrow {AK} ^2} = 4{\overrightarrow {IK} ^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}k - a =  - \frac{k}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\4 + {(k - a)^2} = 4(1 + {k^2})\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)

Thay (1) vào (2) ta được

\(4 + \frac{4}{{{k^2}}} = 4\left( {1 + {k^2}} \right)\) \( \Leftrightarrow 4{k^2} + 4 = 4{k^2} + 4{k^4}\) \( \Leftrightarrow {k^2} = 1 \Leftrightarrow k =  - 1\,\,(k < 0).\)

 Suy ra a = -3.

Vậy A(2 ; -3), C(0 ; 3) và K(0 ; -1).

Ta có \(\overrightarrow {AD}  = 2\overrightarrow {AK} \) \( \Rightarrow \left\{ \begin{array}{l}{x_D} - 2 = 2.(0 - 2)\\{y_D} + 3 = 2.( - 1 + 3)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} = 1.\end{array} \right.\) Vậy D(-2 ; 1)

Ta có \(\overrightarrow {DB}  = 2\overrightarrow {DI}  \Rightarrow \left\{ \begin{array}{l}{x_B} + 2 = 2.(1 + 2)\\{y_B} - 1 = 2.(0 - 1)\end{array} \right. \) \(\Rightarrow \left\{ \begin{array}{l}{x_B} = 4\\{y_B} =  - 1.\end{array} \right.\)

Vậy B(4 ; -1).

Loigiaihay.com