Bài 22 trang 168 SBT toán 9 tập 2

Đề bài

Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng “ hẹp” hoặc một hình trụ rộng nhưng “ thấp”. Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn?

Lời giải chi tiết

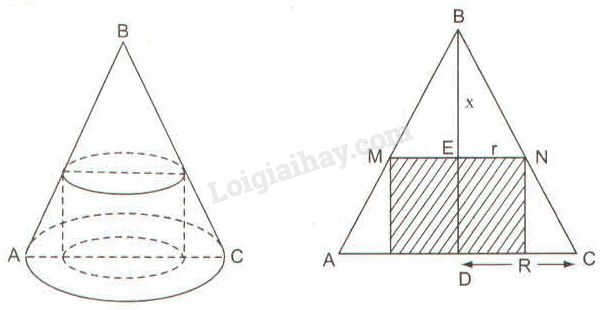
Gọi bán kính đáy hình nón là \(R\), chiều cao hình nón là \(h\), bán kính đáy hình trụ là \(r\), chiều cao phần hình nón cắt đi là \(BE = x\).

Vì \(MN//AC \), theo hệ quả định lí Ta-lét ta có:

\(\displaystyle  {{ME} \over {AD}} = {{BE} \over {BD}}\) hay \(\displaystyle {r \over R} = {x \over h} \Rightarrow r = {{Rx} \over h}\)

Thể tích hình trụ là: \(V = πr^2. (h-x)\)

\(\displaystyle V = \pi .{\left( {{{Rx} \over h}} \right)^2}.\left( {h - x} \right)\)\(\, \displaystyle = \pi .{{{R^2}{x^2}} \over {{h^2}}}.(h - x)\)

Phần bỏ đi của hình nón ít nhất có nghĩa là thể tích của hình trụ lớn nhất:

\(\displaystyle V = \pi .{{{R^2}{x^2}} \over {{h^2}}}(h - x)\)

\(\displaystyle \Rightarrow 2V{h^2} = \pi {R^2}{x^2}(2h - 2x)\)

\(\displaystyle \Rightarrow {{2V{h^2}} \over {\pi {R^2}}} = {x^2}(2h - 2x)\))

Vì \(π, R, h\) là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi \({x^2}\left( {2h - 2x} \right)\) lớn nhất. Ta có \({x^2}\left( {2h - 2x} \right) = x.x.\left( {2h - 2x} \right)\)

Áp dụng bất đẳng thức Cô - si cho ba số dương \(x, x, 2h-2x\) ta có:

\(\sqrt[3]{{x.x.\left( {2h - 2x} \right)}} \le \dfrac{{x + x + 2h - 2x}}{3} = \dfrac{{2h}}{3}\) \( \Rightarrow x.x.\left( {2h - 2x} \right) \le {\left( {\dfrac{{2h}}{3}} \right)^3} \) \(= \dfrac{{8{h^3}}}{{27}}\)

Dấu "=" xảy ra khi \( x = 2h -2x  \Leftrightarrow  3x = 2h  \) \(\Rightarrow  x = \displaystyle {2 \over 3}h\)

Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng \(\displaystyle {2 \over 3}\) chiều cao hình nón thì phần bỏ đi là ít nhất.

Loigiaihay.com