Bài 1.6, 1.7, 1.8, 1.9, 1.10 phần bài tập bổ sung trang 116, 117 SBT toán 7 tập 1

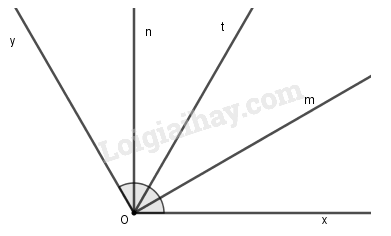
Bài I.6

(A) Hai tia phân giác của cặp góc kề nhau thì vuông góc với nhau

(B) Hai tia phân giác của cặp góc bù nhau thì vuông góc với nhau nhau

(C) Hai tia phân giác của cặp góc đối đỉnh thì vuông góc với

(D) Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau

Phương pháp giải:

Sử dụng tính chất: Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau

Lời giải chi tiết:

Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau

Chọn D.

Bài I.7

Cho góc \(\widehat {xOy} = {120^0}.\) Kẻ \(Ot\) là tia phân giác của \(\widehat {xOy}\). Kẻ tia \(Om\) nằm trong góc \(xOy\) và vuông góc với tia \(Ox.\) Kẻ tia \(On\) nằm trong góc \(xOy\) và vuông góc với tia \(Oy.\) Với hình vẽ được có bao nhiêu góc bằng \({30^0}?\)

(A) 3

(B) 4 

(C) 2

(D) 1

Phương pháp giải:

Sử dụng tính chất tia phân giác và công thức cộng góc

Lời giải chi tiết:

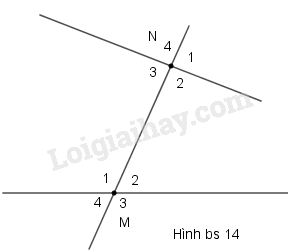
Vì \(Om \bot Oy\) và \(Om\) nằm giữa hai tia \(Ox;Oy\) nên ta có: \(\widehat {xOm} + \widehat {yOm} = \widehat {xOy}\) 

\( \Rightarrow \widehat {xOm} = \widehat {xOy} - \widehat {yOm}\) \( = {120^0} - {90^0} = {30^0}\)

Vì \(On \bot Ox\) và \(On\) nằm giữa hai tia \(Ox;Oy\) nên ta có: \(\widehat {xOn} + \widehat {yOn} = \widehat {xOy}\)

\( \Rightarrow \widehat {yOn} = \widehat {xOy} - \widehat {xOn}\) \( = {120^0} - {90^0} = {30^0}\)

Vì \(Ot\) là tia phân giác \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt}\) \( = \dfrac{1}{2}\widehat {xOy}\)\( = \dfrac{1}{2}{.120^0} = {60^0}\)

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) ta có \(\widehat {xOm} < \widehat {xOt}\) \(\left( {{{30}^0} < {{60}^0}} \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox\) và \(Ot.\)

Suy ra

\(\widehat {xOm} + \widehat {mOt} = \widehat {xOt}\) \( \Rightarrow \widehat {mOt} = \widehat {xOt} - \widehat {xOm}\)\( = {60^0} - {30^0} = {30^0}\)

Trên cùng một nửa mặt phẳng bờ chứa tia \(Oy\) ta có \(\widehat {yOn} < \widehat {yOt}\) \(\left( {{{30}^0} < {{60}^0}} \right)\) nên tia \(On\) nằm giữa hai tia \(Oy\) và \(Ot.\)

Suy ra

\(\widehat {yOn} + \widehat {nOt} = \widehat {yOt}\) \( \Rightarrow \widehat {nOt} = \widehat {yOt} - \widehat {yOn}\)\( = {60^0} - {30^0} = {30^0}\)

Vậy trên hình có 4 góc có số đo bằng \({30^0}.\)

Chọn B.

Bài I.8

Cho hình bs 14. Khi đó:

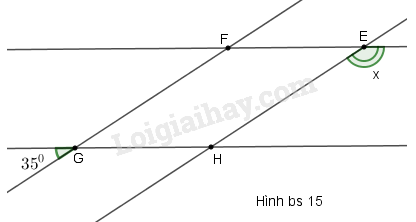
(A) \(\widehat {{N_1}}\) và \(\widehat {{M_1}}\) là hai góc so le trong

(B) \(\widehat {{N_2}}\) và \(\widehat {{M_2}}\) là hai góc đồng vị

(C) \(\widehat {{N_3}}\) và \(\widehat {{M_3}}\) là hai góc so le trong

(D) \(\widehat {{N_4}}\) và \(\widehat {{M_1}}\) là hai góc đồng vị

Phương pháp giải:

Quan sát hình vẽ để nhận ra các góc đồng vị và so le trong 

Lời giải chi tiết:

\(\widehat {{N_4}}\) và \(\widehat {{M_1}}\) là hai góc đồng vị

Chọn D.

Bài I.9

Cho hình bs 15 (hai đường thẳng FE, GH song song với nhau, hai đường thẳng FG, EH song song với nhau). Khi đó, số đo của góc x bằng 

(A) \({35^0}\)

(B) \({145^0}\)

(C) \({155^0}\)

(D) Không tính được

Phương pháp giải:

Một đường thẳng cắt hai đường thẳng song song tạo thành cặp góc đồng vị bằng nhau, cặp góc so le trong bằng nhau và cặp góc trong cùng phía bù nhau.

Lời giải chi tiết:

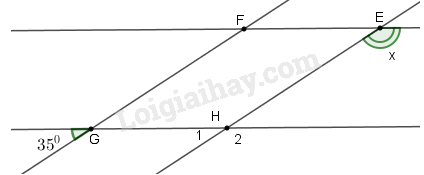
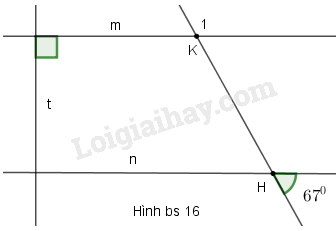
Vì \(EH//FG\) nên \(\widehat {{H_1}} = \widehat G = {35^0}\) (hai góc đồng vị bằng nhau)

Lại có \(\widehat {{H_1}} + \widehat {{H_2}} = {180^0}\) (hai góc kề bù)

\( \Rightarrow \widehat {{H_2}} = {180^0} - \widehat {{H_1}}\) \( = {180^0} - {35^0} = {145^0}\) 

Vì \(HG//EF\) nên \(\widehat E = \widehat {{H_2}} = {145^0}\) (hai góc đồng vị)

Hay \(x = {145^0}.\)

Chọn B.

Bài I.10

Cho hình bs 16 (đường thẳng \(t\) vuông góc với cả hai đường thẳng m, n). Khi đó số đo của góc \(\widehat {{K_1}}\) bằng: 

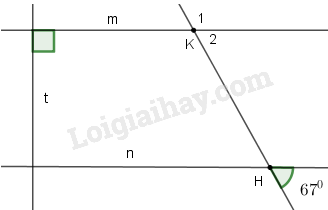
(A) \({67^0}\)

(B) \({90^0}\)

(C) \({113^0}\)

(D) Không tính được

Phương pháp giải:

Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau

Một đường thẳng cắt hai đường thẳng song song tạo thành cặp góc đồng vị bằng nhau, cặp góc so le trong bằng nhau.

Lời giải chi tiết:

Vì \(t \bot m,t \bot n\) nên \(m//n\)  (quan hệ từ vuông góc đến song song)

Suy ra \(\widehat {{K_2}} = \widehat H = {67^0}\) (hai góc đồng vị bằng nhau)

Lại có \(\widehat {{K_1}} + \widehat {{K_2}} = {180^0}\) (hai góc kề bù)

\( \Rightarrow \widehat {{K_1}} = {180^0} - \widehat {{K_2}}\) \( = {180^0} - {67^0} = {113^0}\)

Vậy \(\widehat {{K_1}} = {113^0}\) 

Chọn C.

Loigiaihay.com