Bài 12 trang 8 SBT toán 9 tập 2Giải bài 12 trang 8 sách bài tập toán 9. Minh họa hình học tập nghiệm của mỗi hệ phương trình sau: a)2x+3y=7 và x-y=6; b) 3x+2y=13 và 2x-y= -3; c)x+y=1 và 3x+0y=12; ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
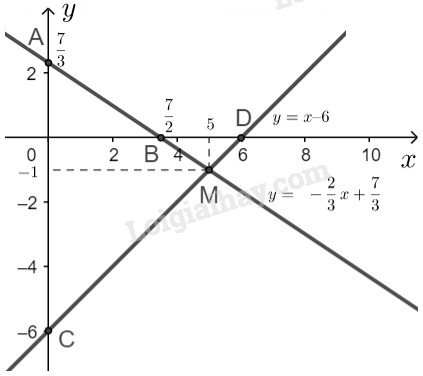
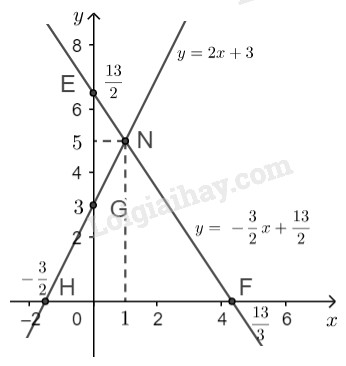
Minh họa hình học tập nghiệm của mỗi hệ phương trình sau: LG a \(\left\{ {\matrix{ Phương pháp giải: Sử dụng: - Ta biến đổi hệ phương trình đã cho về dạng \(\left\{ \begin{array}{l}y = ax + b\\y = a'x + b'\end{array} \right.\) +) Vẽ hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) trong cùng một hệ trục tọa độ. +) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ. +) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ. Lời giải chi tiết: \( \left\{ {\matrix{ - Vẽ đường thẳng \(y = \displaystyle - {2 \over 3}x + {7 \over 3}\): Cho \(x = 0 \Rightarrow y = \displaystyle {7 \over 3}\) ta được \(A\left( {0; \displaystyle{7 \over 3}} \right)\) Cho \(y = 0 \Rightarrow x = \displaystyle {7 \over 2}\) ta được \(B\left( {\displaystyle {7 \over 2};0} \right)\) Đường thẳng \(y = \displaystyle - {2 \over 3}x + {7 \over 3}\) là đường thẳng đi qua hai điểm \(A, \ B.\) - Vẽ đường thẳng \(y = x – 6\): Cho \(x = 0 \Rightarrow y = - 6\) ta được \(C\left( {0; - 6} \right)\) Cho \(y = 0 \Rightarrow x = 6\) ta được \(D\left( {6;0} \right)\) Đường thẳng \(y = x – 6\) là đường thẳng đi qua hai điểm \(C, \ D.\) - Quan sát hình vẽ, ta thấy hai đường thẳng \(y = \displaystyle - {2 \over 3}x + {7 \over 3}\) và \(y = x – 6\) cắt nhau tại điểm \(M (5; -1).\) Thay \(x = 5, y = -1\) vào hệ phương trình đã cho ta được: \(\left\{ \begin{array}{l}2.5 +3.(-1) = 7\\5 - (-1) = 6\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}7 = 7\\ 6 = 6\end{array} \text{(luôn đúng)} \right.\) Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) = (5; -1)\). LG b \( \left\{ {\matrix{ Phương pháp giải: Sử dụng: - Ta biến đổi hệ phương trình đã cho về dạng \(\left\{ \begin{array}{l}y = ax + b\\y = a'x + b'\end{array} \right.\) +) Vẽ hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) trong cùng một hệ trục tọa độ. +) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ. +) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ. Lời giải chi tiết: \(\left\{ {\matrix{ \( \Leftrightarrow \left\{ {\matrix{ - Vẽ đường thẳng \(y = \displaystyle - {3 \over 2}x + {{13} \over 2}\): Cho \(x = 0 \Rightarrow y = \displaystyle {{13} \over 2} \) ta được \(E(0;\displaystyle {{13} \over 2} )\) Cho \(y = 0 \Rightarrow x =\displaystyle {{13} \over 3}\) ta được \(F(\left( {\displaystyle {{13} \over 3};0} \right)\) Đường thẳng \(y = \displaystyle - {3 \over 2}x + {{13} \over 2}\) là đường thẳng đi qua hai điểm \(E, \ F\) - Vẽ đường thẳng \(y = 2x + 3\): Cho \(x = 0 \Rightarrow y = 3\) ta được \(G (0; 3)\) Cho \(y = 0 \Rightarrow x = \displaystyle - {3 \over 2}\) ta được \(H (\displaystyle - {3 \over 2}; 0)\) Đường thẳng \(y = 2x + 3\) là đường thẳng đi qua hai điểm \(G, \ H.\)
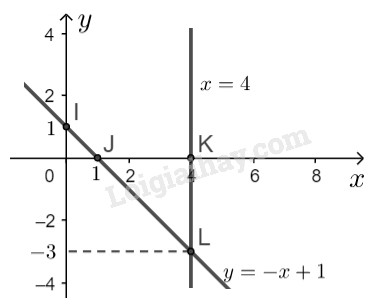
- Quan sát hình vẽ, ta thấy hai đường thẳng \(y = \displaystyle - {3 \over 2}x + {{13} \over 2}\) và \(y = 2x + 3\) cắt nhau tại điểm \(N (1;5).\) Thay \(x = 1, y = 5\) vào hệ phương trình đã cho ta được: \(\left\{ \begin{array}{l}3.1+2.5 = 13\\2.1 - 5 = -3\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}13 = 13\\ -3 = -3\end{array} \text{(luôn đúng)} \right.\) Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) = (1;5)\). LG c \( \left\{ {\matrix{ Phương pháp giải: Sử dụng: - Ta biến đổi hệ phương trình đã cho về dạng \(\left\{ \begin{array}{l}y = ax + b\\y = a'x + b'\end{array} \right.\) +) Vẽ hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) trong cùng một hệ trục tọa độ. +) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ. +) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ. Lời giải chi tiết: \(\left\{ {\matrix{ - Vẽ đường thẳng \(y = -x + 1\): Cho \(x = 0 \Rightarrow y = 1\) ta được \(I (0; 1)\) Cho \(y = 0 \Rightarrow x = 1\) ta được \(J(1; 0)\) Đường thẳng \(y = -x + 1\) là đường thẳng đi qua hai điểm \(I, \ J\). - Vẽ đường thẳng \(x = 4\): Đường thẳng \(x=4\) đi qua điểm \(K(4;0)\) và song song với trục tung.
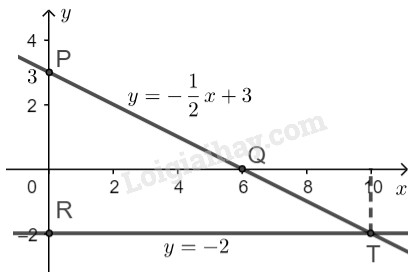
- Quan sát hình vẽ, ta thấy hai đường thẳng \(y = -x + 1\) và \(x = 4\) cắt nhau tại điểm \(L (4;-3).\) Thay \(x = 4, y = -3\) vào hệ phương trình đã cho ta được: \(\left\{ \begin{array}{l}4+(-3)=1\\3.4+0.(-3)=12\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}1= 1\\ 12 = 12\end{array} \text{(luôn đúng)} \right.\) Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) = (4;-3)\). LG d \(\left\{ {\matrix{ Phương pháp giải: Sử dụng: - Ta biến đổi hệ phương trình đã cho về dạng \(\left\{ \begin{array}{l}y = ax + b\\y = a'x + b'\end{array} \right.\) +) Vẽ hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) trong cùng một hệ trục tọa độ. +) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ. +) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ. Lời giải chi tiết: \(\left\{ {\matrix{ \( \Leftrightarrow \left\{ {\matrix{ - Vẽ đường thẳng \(y = \displaystyle - {1 \over 2}x + 3\): Cho \(x = 0 \Rightarrow y = 3\) ta được \(P(0; 3)\) Cho \(y = 0 \Rightarrow x = 6\) ta được \(Q (6; 0)\) Đường thẳng \(y = \displaystyle - {1 \over 2}x + 3\) là đường thẳng đi qua hai điểm \(P, \ Q\). - Vẽ đường thẳng \(y = -2\): Đường thẳng \(y = -2\) đi qua điểm \(R(0;-2)\) và song song với trục hoành.
- Quan sát hình vẽ, ta thấy hai đường thẳng \(y = \displaystyle - {1 \over 2}x + 3\) và \(y = -2\) cắt nhau tại điểm \(T (10;-2).\) Thay \(x = 10, y = -2\) vào hệ phương trình đã cho ta được: \(\left\{ \begin{array}{l}10+2.(-2)=6\\0.10-5.(-2)=10\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}6=6\\ 10 = 10\end{array} \text{(luôn đúng)} \right.\) Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) = (10;-2)\). Loigiaihay.com
|




















Danh sách bình luận