Bài 12 trang 62 SBT toán 9 tập 1

LG câu a

Có tung độ bằng \(5\);

Phương pháp giải:

Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

Lời giải chi tiết:

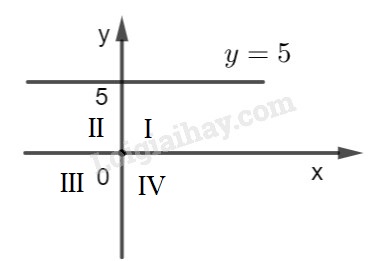
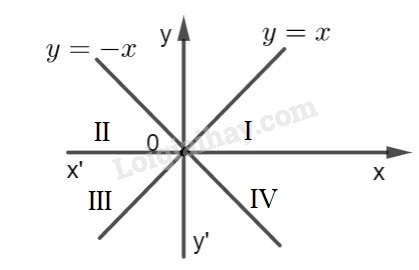
Các điểm có tung độ bằng \(5\) là những điểm nằm trên đường thẳng song song với trục \(Ox\) , cắt trục tung là điểm có tung độ bằng \(5\) (đường thẳng \(y = 5\)).

LG câu b

Có hoành độ bằng \(2\);

Phương pháp giải:

Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

Lời giải chi tiết:

Các điểm có hoành độ bằng \(2\) là những điểm nằm trên đường thẳng song song với trục \(Oy\), cắt trục hoành là điểm có hoành độ bằng \(2\) ( đường thằng \(x = 2\)).

LG câu c

Có tung độ bằng \(0\);

Phương pháp giải:

Chú ý:

- Những điểm trên trục hoành có tung độ  \({y_0} = 0\).

- Những điểm trên trục hoành có tung độ  \({x_0} = 0\).

Lời giải chi tiết:

Các điểm có tung độ bằng \(0\) là những điểm nằm trên trục hoành.

LG câu d

Có hoành độ bằng \(0\);

Phương pháp giải:

Chú ý:

- Những điểm trên trục hoành có tung độ  \({y_0} = 0\).

- Những điểm trên trục hoành có tung độ  \({x_0} = 0\).

Lời giải chi tiết:

Các điểm có hoành độ bằng \(0\) là những điểm nằm trên trục tung.

LG câu e

Có hoành độ và tung độ bằng nhau;

Phương pháp giải:

Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

Lời giải chi tiết:

Các điểm có tung độ và hoành độ bằng nhau là những điểm nằm trên đường thẳng chứa tia phân giác của góc \(xOy\) hay phân giác của góc phần tư số I và góc phần tư số III ( đường thẳng \(y = x\)).

LG câu f

Có hoành độ và tung độ đối nhau;  

Phương pháp giải:

Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

Lời giải chi tiết:

Các điểm có tung độ và hoành độ đối nhau là những điểm nằm trên đường thẳng chứa tia phân giác của góc \(x’Oy\) hay phân giác của góc phần tư số II và góc phần tư  số IV ( đường thẳng \(y = -x\)).

Loigiaihay.com