Bài 107 trang 153 SBT toán 7 tập 1

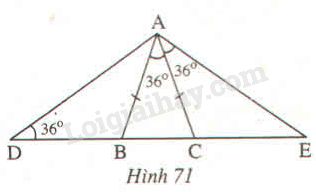
Đề bài

Tìm các tam giác cân trên hình 71.

Lời giải chi tiết

* Vì \(AB = AC\) (gt) nên \(∆ABC\) cân tại \(A.\)

Suy ra \(\widehat {ABC} = \widehat {ACB} \) (tính chất tam giác cân)

Xét tam giác \(ABC\) có:  \(\widehat {ABC} + \widehat {ACB} +\widehat {BAC}=180^0\) (định lý tổng ba góc trong tam giác)

\(\displaystyle \Rightarrow \widehat {ABC} + \widehat {ACB} = 180^\circ  - \widehat {BAC}\)

\(\displaystyle \Rightarrow \widehat {ABC} = \widehat {ACB} = {{180^\circ  - \widehat {BAC}} \over 2} \)\(\,\displaystyle = {{180^\circ  - 36^\circ } \over 2} = 72^\circ \)

Lại có: \(\widehat {BA{\rm{E}}} = \widehat {BAC} + \widehat {CA{\rm{E}}} = 36^\circ  + 36^\circ \)\(\, = 72^\circ \)

\(\Rightarrow \widehat {BA{\rm{E}}} = \widehat {ABE}=72^o\)

\(\Rightarrow ∆ABE\) cân tại \(E\).

* Xét tam giác \(ACE\) có \(\widehat {ACB}\) là góc ngoài tại đỉnh C nên:

\(\widehat E +\widehat {CAE}= \widehat {ACB} \)

\(\Rightarrow \widehat {E} = \widehat {ACB}-\widehat {CAE}\)\(=72^0- 36^\circ=36^0 \)

Do đó \(\widehat {CA{\rm{E}}} = \widehat E=36^o\) nên \(∆ACE\) cân tại \(C.\)

* Áp dụng định lí tổng ba góc của một tam giác vào \(∆DAC\), ta có:

\({\widehat D + \widehat {AC{\rm{D}}}}+\widehat {DAC} = 180^\circ \)

\(\widehat {DAC} = 180^\circ  - \left( {\widehat D + \widehat {AC{\rm{D}}}} \right) \)\(\,= 180^\circ  - \left( {36^\circ  + 72^\circ } \right) = 72^\circ \)

Vì \(\widehat {DAC} = \widehat {AC{\rm{D}}}=72^o\) nên \(∆DAC\) cân tại \(D\).

* Ta có: \(\widehat {DAC} = \widehat {DAB} + \widehat {BAC} \)

\(\Rightarrow \widehat {DAB} = \widehat {DAC} - \widehat {BAC}\)\(\, = 72^\circ - 36^\circ = 36^\circ  \)

\( \Rightarrow \widehat {DAB} = \widehat D=36^o\) nên \(∆ABD\) cân tại \(B\).

* Lại có \(\widehat {A{\rm{D}}E} = \widehat {A{\rm{ED}}} = 36^\circ \) nên \(∆ADE\) cân tại \(A\).

Vậy có \(6\) tam giác cân trong hình 71.

Loigiaihay.com