Giải bài 1 trang 31 sách bài tập toán 12 - Chân trời sáng tạo

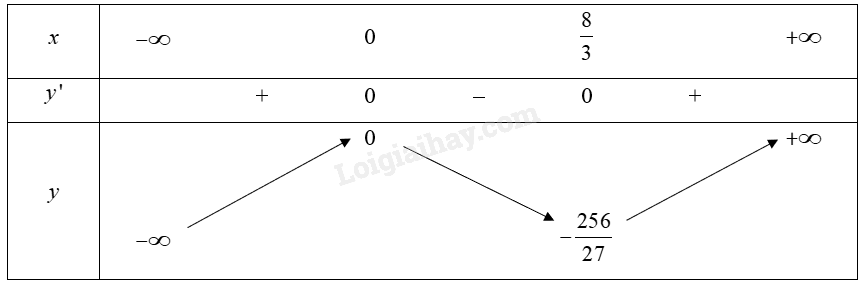
Đề bài

Khảo sát và vẽ đồ thị của các hàm số sau:

a) \(y = x\left( {{x^2} - 4x} \right)\);

b) \(y =  - {x^3} + 3{x^2} - 2\).

Lời giải chi tiết

a) \(y = x\left( {{x^2} - 4x} \right) = {x^3} - 4{x^2}\)

1. Tập xác định: \(\mathbb{R}\).

2. Sự biến thiên:

• Chiều biến thiên:

Đạo hàm \(y' = 3{{\rm{x}}^2} - 8{\rm{x}};y' = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = \frac{8}{3}\).

Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {\frac{8}{3}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên mỗi khoảng đó.

Trên khoảng \(\left( {0;\frac{8}{3}} \right)\), \(y' < 0\) nên hàm số nghịch biến trên khoảng đó.

• Cực trị:

Hàm số đạt cực đại tại \(x = 0\) và ${{y}_{CĐ}}=0$.

Hàm số đạt cực tiểu tại \(x = \frac{8}{3}\) và \({y_{CT}} =  - \frac{{256}}{{27}}\).

• Các giới hạn tại vô cực:

\(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } {x^3}\left( {1 - \frac{4}{x}} \right) =  - \infty ;\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {x^3}\left( {1 - \frac{4}{x}} \right) =  + \infty \).

• Bảng biến thiên:

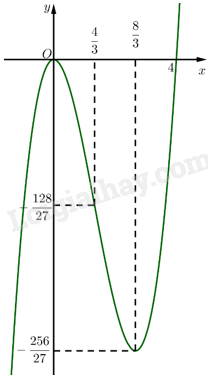
3. Đồ thị

Khi \(x = 0\) thì \(y = 0\) nên \(\left( {0;0} \right)\) là giao điểm của đồ thị với trục \(Oy\).

Ta có \(y = 0 \Leftrightarrow {x^3} - 4{{\rm{x}}^2} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 4\).

Vậy đồ thị hàm số giao với trục \(Ox\) tại hai điểm \(\left( {0;0} \right)\) và \(\left( {4;0} \right)\).

Điểm \(\left( {0;0} \right)\) là điểm cực đại và điểm \(\left( {\frac{8}{3}; - \frac{{256}}{{27}}} \right)\) là điểm cực tiểu của đồ thị hàm số.

Vậy đồ thị hàm số được biểu diễn như hình vẽ bên.

Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( {\frac{4}{3}; - \frac{{128}}{{27}}} \right)\).

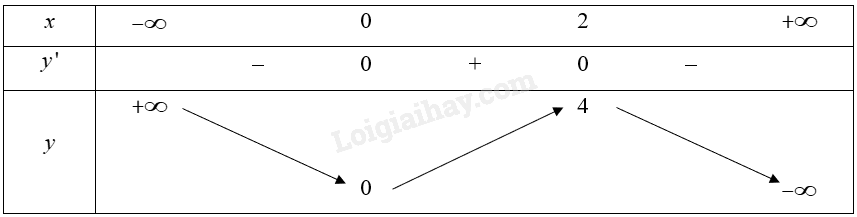
b) \(y =  - {x^3} + 3{x^2} - 2\)

1. Tập xác định: \(\mathbb{R}\).

2. Sự biến thiên:

• Chiều biến thiên:

Đạo hàm \(y' =  - 3{{\rm{x}}^2} + 6{\rm{x}};y' = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 2\).

Trên khoảng \(\left( {0;2} \right)\), \(y' > 0\) nên hàm số đồng biến trên khoảng đó.

Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), \(y' < 0\) nên hàm số nghịch biến trên mỗi khoảng đó.

• Cực trị:

Hàm số đạt cực đại tại \(x = 2\) và ${{y}_{CĐ}}=4$.

Hàm số đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = 0\).

• Các giới hạn tại vô cực:

\(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } {x^3}\left( { - 1 + \frac{3}{x} - \frac{2}{{{x^3}}}} \right) =  + \infty ;\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {x^3}\left( { - 1 + \frac{3}{x} - \frac{2}{{{x^3}}}} \right) =  - \infty \).

• Bảng biến thiên:

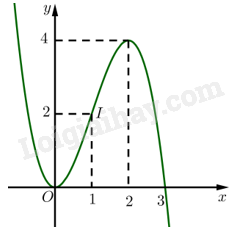
3. Đồ thị

Khi \(x = 0\) thì \(y = 0\) nên \(\left( {0;0} \right)\) là giao điểm của đồ thị với trục \(Oy\).

Ta có \(y = 0 \Leftrightarrow  - {x^3} + 3{{\rm{x}}^2} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 3\).

Vậy đồ thị hàm số giao với trục \(Ox\) tại hai điểm \(\left( {0;0} \right)\) và \(\left( {3;0} \right)\).

Điểm \(\left( {2;4} \right)\) là điểm cực đại và điểm \(\left( {0;0} \right)\) là điểm cực tiểu của đồ thị hàm số.

Vậy đồ thị hàm số được biểu diễn như hình vẽ bên.

Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( {2;2} \right)\).