Đề thi học kì 2 Toán 8 - Đề số 3 - Chân trời sáng tạoPhần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn làĐề bài
I. Trắc nghiệm
Câu 1 :
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Câu 2 :
Phương trình nào sau đây nhận \(m = 2\) là nghiệm?
Câu 3 :
Phương trình \(x + 5 = x + 5\) có
Câu 4 :
Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là
Câu 5 :
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 5” là thẻ
Câu 6 :
Bạn An gieo một con xúc xắc 50 lần và thống kê kết quả các lần gieo ở bảng sau:
Xác suất thực nghiệm của biến cố “Gieo được mặt số chấm là số nguyên tố” là
Câu 8 :
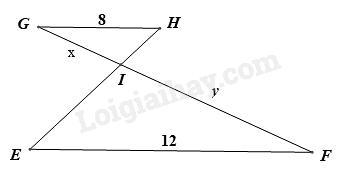
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:
Câu 9 :
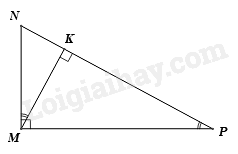
Cho hình vẽ
Khi đó các khẳng định sau (1) $\Delta MKN\backsim \Delta PKM\text{ (g}\text{.g)}$. (2) $\Delta MKP\backsim \Delta MNP\text{ (g}\text{.g)}$. Hãy chọn đáp án đúng:
Câu 10 :
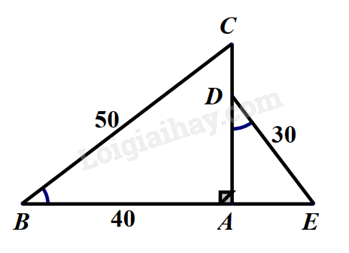
Cho hình vẽ sau, biết \(\widehat B = \widehat D,BC = 50cm,AB = 40cm,DE = 30cm\). Độ dài đoạn thẳng AD là:
Câu 11 :
Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?
Câu 12 :
Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Đáp án : A Phương pháp giải :
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\). Lời giải chi tiết :
Phương trình bậc nhất một ẩn là phương trình \(2x + 1 = 0\). Đáp án A.
Câu 2 :
Phương trình nào sau đây nhận \(m = 2\) là nghiệm?
Đáp án : A Phương pháp giải :
Thay m = 2 vào phương trình để xác định. Lời giải chi tiết :
Ta có: 2 – 2 = 0 nên phương trình m – 2 nhận m = 2 là nghiệm. Đáp án A.
Câu 3 :
Phương trình \(x + 5 = x + 5\) có
Đáp án : A Phương pháp giải :
Giải phương trình để tìm nghiệm. Lời giải chi tiết :
\(\begin{array}{l}x + 5 = x + 5\\x - x = 5 - 5\end{array}\) \(0 = 0\) (luôn đúng) Vậy phương trình \(x + 5 = x + 5\) có vô số nghiệm. Đáp án A.
Câu 4 :
Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là
Đáp án : C Phương pháp giải :
Gọi tuổi con hiện tại là x. Lập phương trình. Giải phương trình để tìm tuổi con. Kiểm tra kết quả. Lời giải chi tiết :
Gọi tuổi của con hiện tại là x \(\left( {x > 1,x \in N*} \right)\) Vì năm nay cha 39 tuổi và gấp 3 lần tuổi con năm ngoái nên ta có phương trình: \(\begin{array}{l}3\left( {x - 1} \right) = 39\\x - 1 = 13\\x = 14(TM)\end{array}\) Vậy năm nay con 14 tuổi. Đáp án C.
Câu 5 :
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 5” là thẻ
Đáp án : D Phương pháp giải :
Xác định kết quả thuận lợi cho biến cố. Lời giải chi tiết :
Vì chỉ có \(5 \vdots 5\) nên kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 5” là thẻ ghi số 5. Đáp án D.
Câu 6 :
Bạn An gieo một con xúc xắc 50 lần và thống kê kết quả các lần gieo ở bảng sau:
Xác suất thực nghiệm của biến cố “Gieo được mặt số chấm là số nguyên tố” là
Đáp án : B Phương pháp giải :
Tính số lần xuất hiện mặt chấm là số nguyên tố. Tính xác suất thực nghiệm của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả. Lời giải chi tiết :
Các số nguyên tố là 2; 3; 5. Số lần xuất hiện mặt chấm là số nguyên tố là: 8 + 6 + 4 = 18 Xác suất thực nghiệm của biến cố “Gieo được mặt số chấm là số nguyên tố” là: \(\frac{{18}}{{50}} = \frac{9}{{25}}\) Đáp án B.
Đáp án : A Phương pháp giải :
Chứng minh hai tam giác đồng dạng theo trường hợp c.g.c. Lời giải chi tiết :
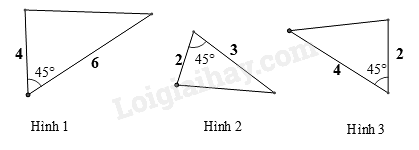
Xét hình 1 và hình 2 có một góc \({45^0}\), tỉ số hai cạnh kề góc dó là \(\frac{4}{6} = \frac{2}{3}\) nên hình 1 và hình 2 là hai tam giác đồng dạng. Xét hình 1 và hình 2 có một góc \({45^0}\), tỉ số hai cạnh kề góc dó là \(\frac{4}{6} = \frac{2}{3} \ne \frac{2}{4}\) nên hình 1 và hình 3 không là hai tam giác đồng dạng. Từ đó suy ra hình 2 và hình 3 cũng không đồng dạng. Vậy A đúng. Đáp án A.
Câu 8 :
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:
Đáp án : C Phương pháp giải :
Từ hai tam giác đồng dạng suy ra tỉ số đồng dạng Lời giải chi tiết :
Vì $\Delta GHI\backsim \Delta FEI$ nên \(\frac{y}{x} = \frac{{IF}}{{GI}} = \frac{{EF}}{{GH}} = \frac{{12}}{8} = \frac{3}{2}\). Đáp án C.
Câu 9 :
Cho hình vẽ
Khi đó các khẳng định sau (1) $\Delta MKN\backsim \Delta PKM\text{ (g}\text{.g)}$. (2) $\Delta MKP\backsim \Delta MNP\text{ (g}\text{.g)}$. Hãy chọn đáp án đúng:
Đáp án : A Phương pháp giải :
Xác định xem \(\Delta MKN\backsim \Delta PKM\) và $\Delta MKP\backsim \Delta MNP$ có đúng hay không. Lời giải chi tiết :
\(\Delta MKN\) và \(\Delta PKM\) có \(\widehat N\) chung, \(\widehat M = \widehat K = {90^0}\) nên \(\Delta MKN\backsim \Delta PKM\) (g.g) suy ra khẳng định (1) đúng. Tương tự $\Delta MKP\backsim \Delta NMP$ (g.g). Khẳng định (2) không đúng vì các đỉnh của hai tam giác đồng dạng chưa được viết chính xác. Vậy chỉ có khẳng định (1) đúng. Đáp án A.
Câu 10 :
Cho hình vẽ sau, biết \(\widehat B = \widehat D,BC = 50cm,AB = 40cm,DE = 30cm\). Độ dài đoạn thẳng AD là:
Đáp án : B Phương pháp giải :
Chứng minh $\Delta ABC\backsim \Delta ADE$ suy ra tỉ số giữa các cạnh tương ứng. Lời giải chi tiết :
Xét \(\Delta ABC\) và \(\Delta ADE\) có: \(\widehat B = \widehat D\) \(\widehat {CAB} = \widehat {EAD}\left( { = {{90}^0}} \right)\) Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g) suy ra \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{40}}{{50}} = \frac{{AD}}{{30}}\) suy ra \(AD = 30.\frac{{40}}{{50}} = 24\)(cm). Đáp án B.
Câu 11 :
Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?
Đáp án : D Phương pháp giải :
Dựa vào đặc điểm của các hình để xác định. Lời giải chi tiết :
Trong các hình trên chỉ có hình vuông là hình có các cạnh bằng nhau, các góc bằng nhau nên luôn đồng dạng. Đáp án D.
Câu 12 :
Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:
Đáp án : B Phương pháp giải :
Dựa vào tỉ số k tính kích thước cạnh hình b. Lời giải chi tiết :
Vì hình b là hình a sau khi phóng to với kích thước k = 2 nên cạnh của hình b gấp 2 lần cạnh của hình a. Ta có: 3.2 = 6; 4.2 = 8 \( \Rightarrow \) Kích thước hình b là 6 x 8. Đáp án B.
II. Tự luận
Phương pháp giải :
a, b) Đưa phương trình về dạng \(ax + b = 0\) để giải. c, d) Quy đồng bỏ mẫu đưa phương trình về dạng \(ax + b = 0\) để giải. Lời giải chi tiết :
a) \(2x - 4 = 3x + 1\) \(\begin{array}{l}2x - 3x = 1 + 4\\ - x = 5\\x = - 5\end{array}\) Vậy \(x = - 5\). b) \(7\left( {5 - x} \right) = 11 - 5x\) \(\begin{array}{l}35 - 7x = 11 - 5x\\ - 7x + 5x = 11 - 35\\ - 2x = - 24\\x = 12\end{array}\) Vậy \(x = 12\). c) \(\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}\) \(\begin{array}{l}\frac{{10}}{{12}} + \frac{{3x}}{{12}} = \frac{{24}}{{12}} - \frac{{4x}}{{12}}\\10 + 3x = 24 - 4x\\3x + 4x = 24 - 10\\7x = 14\\x = 2\end{array}\) Vậy \(x = 2\). d) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{5} + \frac{1}{2}\) \(\begin{array}{l}\frac{{10.2\left( {x + 1} \right)}}{{30}} = \frac{{6\left( {1 + 3x} \right)}}{{30}} + \frac{{15}}{{30}}\\20\left( {x + 1} \right) = 6\left( {1 + 3x} \right) + 15\\20x + 20 = 6 + 18x + 15\\20x - 18x = 6 + 15 - 20\\2x = 1\\x = \frac{1}{2}\end{array}\) Vậy \(x = \frac{1}{2}\). Phương pháp giải :
Giải bài toán bằng cách lập phương trình. Gọi nồng độ muối trong dung dịch I là x (%) (x > 0) Biểu diễn nồng độ muối trong dung dịch II, khối lượng muối trong hai dung dịch theo x và lập phương trình (Sử dụng công thức \(C\% = \frac{{{m_{ct}}.100\% }}{{{m_{hh}}}}\)). Giải phương trình và kiểm tra nghiệm. Lời giải chi tiết :
Gọi nồng độ muối trong dung dịch I là \(x\left( \% \right)\left( {x > 0} \right)\). Khi đó khối lượng muối có trong dung dịch I là: \(200.x\% = 200\frac{x}{{100}} = 2x\)(g). Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là \(x - 20\left( \% \right)\) Khi đó khối lượng muối có trong dung dịch II là: \(300.\left( {x - 20} \right)\% = 300.\frac{{x - 20}}{{100}} = 3\left( {x - 20} \right)\)(g). Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là: \(2x + 3\left( {x - 20} \right)\)(g). Khối lượng dung dịch muối sau khi trộn hai dung dịch là: \(200 + 300 = 500\)(g). Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình: \(\frac{{2x + 3\left( {x - 20} \right)}}{{500}}.100\% = 33\% \) hay \(2x + 3\left( {x - 20} \right) = 165\) Giải phương trình ta được \(x = 45\)(thỏa mãn). Suy ra nồng độ muối trong dung dịch II là: \(40 - 20 = 25\left( \% \right)\) Vậy nồng độ muối của dung dịch I và II lần lượt là 45% và 25%. Phương pháp giải :
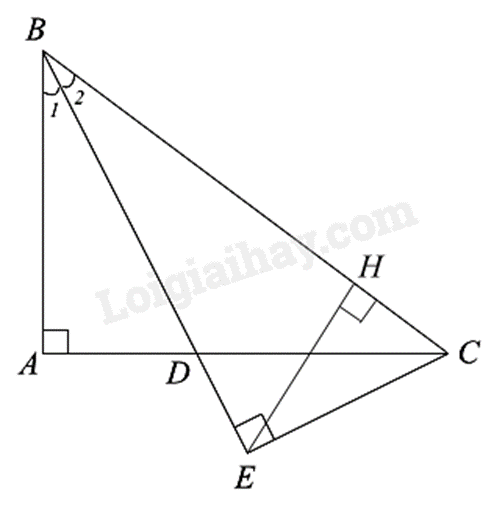
a) Sử dụng định lí Pythagore để tính BC, sử dụng tính chất tia phân giác để tính \(\frac{{AD}}{{DC}}\). b) Chứng minh $\Delta ABD\backsim \Delta EBC$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng. c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}} = \frac{{AD}}{{AB}}\) d) Chứng minh \(CH.CB = ED.EB = C{E^2}\) Lời giải chi tiết :
a) Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) Suy ra \(BC = \sqrt {100} = 10\) (cm). Vì BD là tia phân giác của góc ABC nên ta có: \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\) b) Theo đề bài, \(CE \bot BD\) tại E nên \(\widehat {BEC} = {90^0}\) Xét \(\Delta ABD\) và \(\Delta EBC\) có: \(\widehat {BAD} = \widehat {BEC} = {90^0}\) \(\widehat {{B_1}} = \widehat {{B_2}}\) (BD là tia phân giác của góc ABC) Suy ra $\Delta ABD\backsim \Delta EBC$ (g.g) (đpcm) Suy ra \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số các cạnh tương ứng) Do đó \(BD.EC = AD.BC\) (đpcm) c) Vì \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}\) nên \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\) (1) Vì $\Delta ABD\backsim \Delta EBC$ (cmt) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}}\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\) (2) Từ (1) và (2) suy ra \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\) (đpcm) d) Xét \(\Delta CHE\) và \(\Delta CEB\) có: \(\widehat {CHE} = \widehat {CEB} = {90^0}\) \(\widehat C\) chung Suy ra $\Delta CHE\backsim \Delta CEB$ (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}\) suy ra \(CH.CB = C{E^2}\) (3) Tương tự, $\Delta CDE\backsim \Delta BCE$ (g.g) nên \(\frac{{ED}}{{EC}} = \frac{{CE}}{{BE}}\) suy ra \(ED.EB = C{E^2}\)(4) Từ (3) và (4) suy ra \(CH.CB = ED.EB\) (đpcm) Phương pháp giải :
Gọi chiều dài của mảnh vườn là x. Biểu thị chiều rộng mảnh vườn theo x và giải phương trình. Lời giải chi tiết :
Gọi chiều dài của mảnh vườn là x (m), x > 3. Chiều rộng của mảnh vườn là: x – 3 (m) Vì chu vi của mảnh vườn hình chữ nhật là 42m nên ta có phương trình: \(\begin{array}{l}2\left[ {x + \left( {x - 3} \right)} \right] = 42\\2x - 3 = 21\\2x = 24\\x = 12\left( {TM} \right)\end{array}\) Vậy chiều dài của mảnh vườn là 12 m. Phương pháp giải :
Phân tích \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}} = \frac{1}{{{k^2}}} - \frac{1}{{{{\left( {k + 1} \right)}^2}}}\) Từ đó tính \({S_{2024}}\). Lời giải chi tiết :
Ta có: \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}} = \frac{{{{\left( {k + 1} \right)}^2} - {k^2}}}{{{k^2}{{\left( {k + 1} \right)}^2}}} = \frac{1}{{{k^2}}} - \frac{1}{{{{\left( {k + 1} \right)}^2}}}\) Do đó: \(\begin{array}{l}{S_{2024}} = {a_1} + {a_2} + {a_3} + ... + {a_{2024}}\\ = \left( {\frac{1}{{{1^2}}} - \frac{1}{{{2^2}}}} \right) + \left( {\frac{1}{{{2^2}}} - \frac{1}{{{3^2}}}} \right) + \left( {\frac{1}{{{3^2}}} - \frac{1}{{{4^2}}}} \right) + ... + \left( {\frac{1}{{{{2023}^2}}} - \frac{1}{{{{2024}^2}}}} \right)\\ = 1 - \frac{1}{{{{2024}^2}}}\\ = \frac{{{{2024}^2} - 1}}{{{{2024}^2}}}\end{array}\) Vậy \({S_{2024}} = \frac{{{{2024}^2} - 1}}{{{{2024}^2}}}\)
|


























Danh sách bình luận