Đề thi giữa kì 2 Toán 8 - Đề số 3 - Chân trời sáng tạoTổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Câu 1: (150980) Câu nào sau đây đúng:Đề bài
I. Trắc nghiệm
Câu 1 :
Câu nào sau đây đúng :
Câu 2 :
Đồ thị của hàm số y = \(\frac{1}{3}\)x là đường thẳng OA với O ( 0 ; 0 ) và
Câu 3 :
Các nhà khoa học đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt Trái Đất như sau: T = 0,02t + 15. Trong đó T là nhiệt độ trung bình của bề mặt Trái Đất tính theo độ C, t là số năm kể từ năm 1950. Nhiệt độ trung bình của bề mặt Trái Đất vào năm 1950 và năm 2022 lần lượt là :
Câu 5 :
Giá trị của hàm số \(f\left( x \right) = {x^2} - 1\). Giá trị \(f\left( 2 \right)\) bằng:
Câu 6 :
Hệ số góc của hàm số \(y = 4x + 5\) là:
Câu 7 :
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
Câu 8 :
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.
Câu 9 :
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
Câu 10 :
Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
Câu 12 :
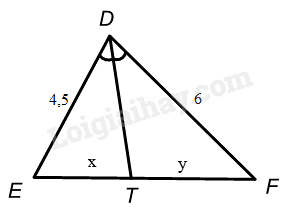
Cho hình vẽ sau, biết DT là tia phân giác của \(\widehat {EDF}\). Tỉ số \(\frac{x}{y}\) bằng:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Câu nào sau đây đúng :
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về đồ thị để kiểm tra. Lời giải chi tiết :
Gốc tọa độ là điểm O(0;0) nên A đúng. Điểm nằm trên trục hoành có tung độ bằng 0 và điểm nằm trên trục tung có hoành độ bằng 0 nên B, C đúng.
Câu 2 :
Đồ thị của hàm số y = \(\frac{1}{3}\)x là đường thẳng OA với O ( 0 ; 0 ) và
Đáp án : C Phương pháp giải :
Thay tọa độ điểm A vào hàm số để xem A có thuộc hàm số hay không. Lời giải chi tiết :
Với \(x = 1 \Rightarrow y = \frac{1}{3}.1 = \frac{1}{3} \ne 3\) nên điểm A(1;3) không thuộc đồ thị hàm số y = \(\frac{1}{3}\)x. Với \(x = - 1 \Rightarrow y = \frac{1}{3}.\left( { - 1} \right) = - \frac{1}{3} \ne - 3\) nên điểm A(-1;-3) không thuộc đồ thị hàm số y = \(\frac{1}{3}\)x. Với \(x = 3 \Rightarrow y = \frac{1}{3}.3 = 1\) nên điểm A(3;1) thuộc đồ thị hàm số y = \(\frac{1}{3}\)x. Với \(x = - 3 \Rightarrow y = \frac{1}{3}.\left( { - 3} \right) = - 1 \ne 1\) nên điểm A(-3;1) không thuộc đồ thị hàm số y = \(\frac{1}{3}\)x.
Câu 3 :
Các nhà khoa học đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt Trái Đất như sau: T = 0,02t + 15. Trong đó T là nhiệt độ trung bình của bề mặt Trái Đất tính theo độ C, t là số năm kể từ năm 1950. Nhiệt độ trung bình của bề mặt Trái Đất vào năm 1950 và năm 2022 lần lượt là :
Đáp án : A Phương pháp giải :
Thay t = 1950 – 1950 = 0 và t = 2022 – 1950 = 72 để tính nhiệt độ. Lời giải chi tiết :
Vào năm 1950, t = 1950 – 1950 = 0 \( \Rightarrow \) T = 0,02.0 + 15 = 15 (0C). Vào năm 2022, t = 2022 – 1950 = 72 \( \Rightarrow \) T = 0,02.72 + 15 = 16,44 (0C).
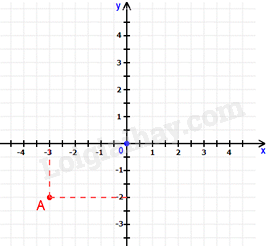
Đáp án : A Phương pháp giải :
Quan sát đồ thị để xác định. Lời giải chi tiết :
Hình chiếu của điểm A trên trục hoành là -3, trên trục tung là -2 nên tọa độ điểm A là A(-3; -2).
Câu 5 :
Giá trị của hàm số \(f\left( x \right) = {x^2} - 1\). Giá trị \(f\left( 2 \right)\) bằng:
Đáp án : B Phương pháp giải :
Thay x = 2 vào f(x) để tìm giá trị f(2). Lời giải chi tiết :
Giá trị f(2) là: \(f\left( 2 \right) = {2^2} - 1 = 3\).
Câu 6 :
Hệ số góc của hàm số \(y = 4x + 5\) là:
Đáp án : B Phương pháp giải :
Hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) có a là hệ số góc. Lời giải chi tiết :
Hệ số góc của hàm số \(y = 4x + 5\) là 4.
Câu 7 :
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
Đáp án : C Phương pháp giải :
Sử dụng tính chất đường trung bình. Lời giải chi tiết :
Ta có M, N là trung điểm các cạnh AB, AC của tam giác ABC nên MN là đường trung bình của tam giác ABC, khi đó MN = \(\frac{1}{2}\)BC. Mà MN = 8cm nên BC = 8.2 = 16 cm.
Câu 8 :
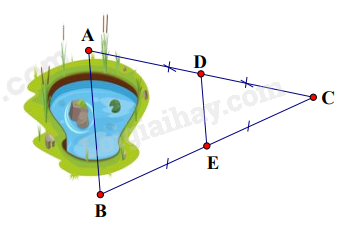
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.
Đáp án : A Phương pháp giải :
Sử dụng tính chất của đường trung bình trong tam giác. Lời giải chi tiết :
Theo hình vẽ, ta thấy AD = DC; BE = EC nên D là trung điểm của AC và E là trung điểm của BC. Khi đó DE là đường trung bình của tam giác ABC => DE = \(\frac{1}{2}\)AB. Mà DE = 100m => AB = 2.100 = 200(m).
Câu 9 :
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
Đáp án : B Phương pháp giải :
Sử dụng định lí Thales đảo để chứng minh. Lời giải chi tiết :
Tam giác ABC cân tại A nên AB = AC. Vì BM = CN; AB = AC nên AB – BM = AC – CN hay AM = AN Suy ra \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) => MN // BC (định lí Thales đảo). Khi đó BMNC là hình thang. Mà BM = CN nên BMNC là hình thang cân.
Câu 10 :
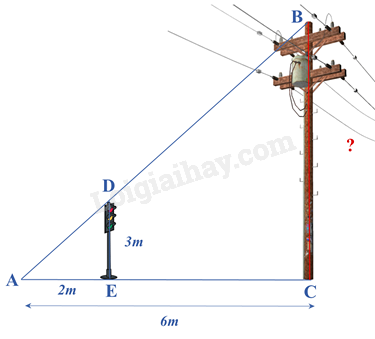
Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
Đáp án : C Phương pháp giải :
Áp dụng hệ quả của định lí Thales trong tam giác. Lời giải chi tiết :
Vì cột đèn giao thông và cột điện cùng vuông góc với mặt đất nên song song với nhau. \( \Rightarrow DE//BC\). Áp dụng hệ quả của định lí Thales trong tam giác, ta có: \(\begin{array}{l}\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\\frac{2}{6} = \frac{3}{{BC}} \Rightarrow BC = 3:\frac{2}{6} = 9\left( m \right)\end{array}\)
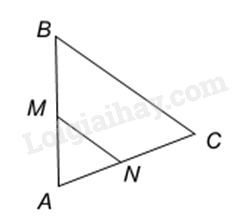
Đáp án : A Phương pháp giải :
Áp dụng định lí Thales trong tam giác. Lời giải chi tiết :
Xét tam giác ABC có MN // BC \( \Rightarrow \frac{{AM}}{{BM}} = \frac{{AN}}{{NC}}\)
Câu 12 :
Cho hình vẽ sau, biết DT là tia phân giác của \(\widehat {EDF}\). Tỉ số \(\frac{x}{y}\) bằng:
Đáp án : B Phương pháp giải :
Dựa vào tính chất đường phân giác trong tam giác. Lời giải chi tiết :
Ta có DT là tia phân giác của \(\widehat {EDF}\) nên ta có: \(\frac{{DE}}{{ET}} = \frac{{DF}}{{TF}} \Rightarrow \frac{x}{y} = \frac{{ET}}{{TF}} = \frac{{DE}}{{DF}} = \frac{{4,5}}{6} = \frac{3}{4}\) (theo tính chất của đường phân giác)
II. Tự luận
Phương pháp giải :
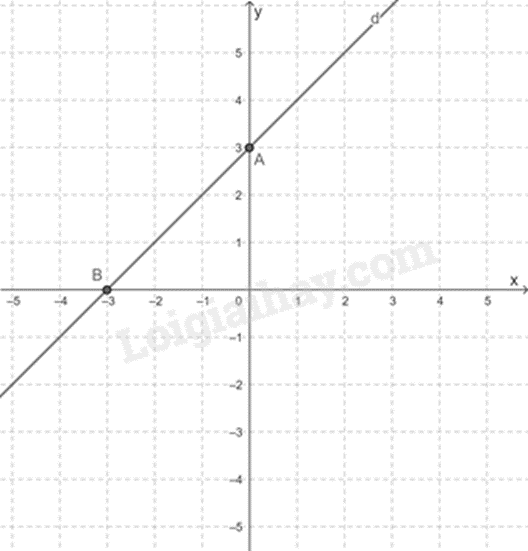
a) Lấy hai điểm thuộc đồ thị hàm số để vẽ đồ thị, b) Viết phương trình hoành độ giao điểm của hai đường thẳng để tìm giao điểm. c) Để hàm số y = (3 - 2m)x + 2 song song với (d) thì 3 – 2m = 1. Lời giải chi tiết :
a) Cho x = 0 thì y = 0 + 3 = 3. Ta được điểm A(0; 3). Cho y = 0 thì 0 = x + 3 => x = -3. Ta được điểm B(-3; 0). Đường thẳng AB chính là đồ thị (d) của hàm số y = x + 3.
b) Phương trình tọa độ giao điểm của (d) và đường thẳng y = -x + 1 là: x + 3 = -x + 1 \( \Leftrightarrow \) 2x = -2 \( \Leftrightarrow \) x = -1. Với x = -1 => y = -1 + 3 = 2. Ta được điểm C(-1; 2). Vậy giao điểm của (d) và đường thẳng y = -x + 1 là C(-1; 2). c) Để hàm số y = (3 - 2m)x + 2 song song với (d) thì 3 – 2m = 1 hay m = 1. Vậy m = 1 thì hàm số y = (3 - 2m)x + 2 song song với (d). Phương pháp giải :
a) 1 thanh giá 40 000 đồng suy ra số tiền mua x thanh. Kiểm tra xem hàm số y có dạng \(y = ax + b\left( {a \ne 0} \right)\) hay không. b) Thay y = 480 000 để tìm x. Lời giải chi tiết :
a) Số tiền bỏ ra để mua 1 thanh lò xo là 40 000 đồng. Số tiền bỏ ra để mua x thanh lò xo là: y = 40 000x (đồng) Vì y có dạng y = ax + b và 40 000 \( \ne \) 0 nên y là hàm số bậc nhất của x. b) Bạn A mua hết 480 000 đồng nên thay y = 480 000 ta được: \(\begin{array}{l}40\,000x = 480\,000\\ \Rightarrow x = 12\end{array}\) Vậy bạn A đã mua 12 thanh lò xo. Phương pháp giải :
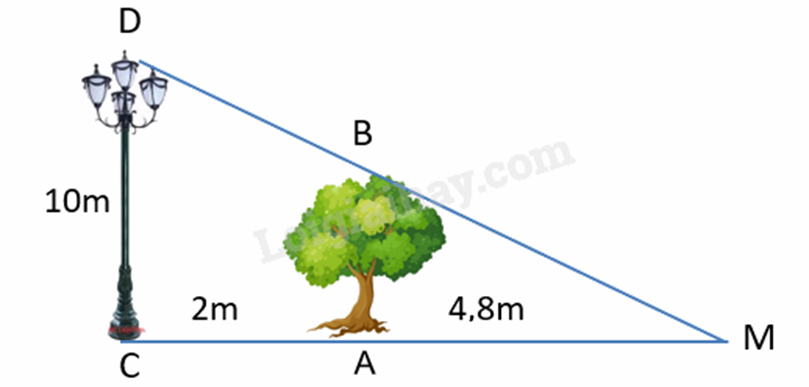
Áp dụng hệ quả của định lí Thales để tính chiều cao cây xanh. Lời giải chi tiết :
Khoảng cách từ điểm C đến điểm M là: 2 + 4,8 = 6,8 (m). Vì cột đèn và cái cây đều vuông góc với mặt đất nên ta có AB // CD. Xét tam giác CMD có AB // CD nên: \(\begin{array}{l}\frac{{AB}}{{AM}} = \frac{{CD}}{{CM}}\\\frac{{AB}}{{4,8}} = \frac{{10}}{{6,8}} \Rightarrow AB = 4,8.\frac{{10}}{{6,8}} = \frac{{120}}{{17}} \approx 7\left( m \right)\end{array}\) Vậy chiều cao của cây xanh là khoảng 7m. Phương pháp giải :
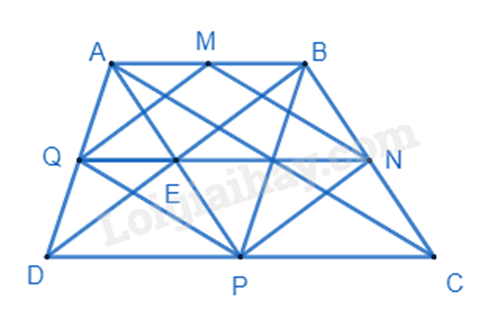
1. Dựa vào tính chất đường phân giác, sử dụng tỉ số bằng nhau để tính. 2. a) Dựa vào dấu hiệu nhận biết hình bình hành và tính chất đường trung bình để chứng minh. b) Dựa vào dấu hiệu nhận biết hình thoi và tính chất đường trung bình. c) Sử dụng tính chất đường trung bình để chứng minh EQ // AB và EN // AB suy ra Q, N, E thẳng hàng. Lời giải chi tiết :
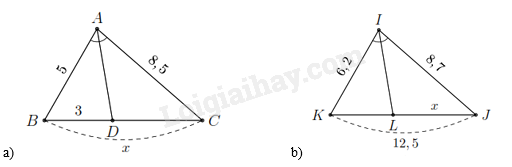
1. a)
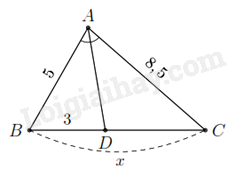
Do \(AD\) là đường phân giác trong của góc \(A\) nên ta có \(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}} \Rightarrow DC = \frac{{AC}}{{AB}} \cdot DB.\) Thay số ta có \(DC = \frac{{8,5}}{5} \cdot 3 = 5,1\). Khi đó \(x = DB + DC = 3 + 5,1 = 8,1\). b)
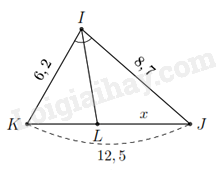
Với \(KL = 12,5 - x\) và do \(IL\) là đường phân giác trong của góc \(I\) nên theo tính chất đường phân giác ta có Theo tính chất đường phân giác ta có \(\frac{{KL}}{{LJ}} = \frac{{IK}}{{IJ}} \Rightarrow \frac{{12,5 - x}}{x} = \frac{{6,2}}{{8,7}} \Leftrightarrow x = \frac{{2175}}{{298}} \approx 7,3\). 2.
a) Ta có: \(DP = \frac{1}{2}DC = AB\); \(AB//CD \Rightarrow AB//DP\) nên ABPD là hình bình hành. Vẽ AC, ta có MN là đường trung bình \(\Delta ABC \Rightarrow MN = \frac{1}{2}AC;MN//AC\). Chứng minh tương tự \( \Rightarrow PQ = \frac{1}{2}AC;PQ//AC\). \( \Rightarrow MN = PQ;PQ//AC\) nên MNPQ là hình bình hành. b) Tương tự như đường chéo AC, vẽ BD, ta cũng chứng minh được MQ và NP là đường trung bình của tam giác ABD và BCD nên \(MQ = NP = \frac{1}{2}BD;MQ//NP//BD\). MNPQ là hình thoi khi MN = MQ mà \(MN = \frac{1}{2}AC;MQ = \frac{1}{2}BD\) (tính chất đường trung bình) \( \Rightarrow AC = BD\). Khi đó ABCD là hình thang cân. c) Vì ABPD là hình bình hành nên E là trung điểm của AP. Xét tam giác ABD có QE là đường trung bình của tam giác ABD nên QE // AB (1) Xét tam giác DBC có EN là đường trung bình của tam giác DBC nên EN // DC mà DC // AB nên EN // AB (2) Từ (1) và (2) suy ra từ E kẻ được EQ // AB và EN // AB nên Q, E, N thẳng hàng Phương pháp giải :
Áp dụng đẳng thức \(\frac{1}{a} - \frac{1}{b} = \frac{{b - a}}{{ab}}\) Lời giải chi tiết :
Xét phân thức \(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c - a + b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{a - b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{1}{{a - b}} - \frac{1}{{a - c}}\). Tương tự ta có: \(\frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} = \frac{1}{{b - c}} - \frac{1}{{b - a}}\) \(\frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{1}{{c - a}} - \frac{1}{{c - b}}\) \( \Rightarrow \frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}}\) \( = \frac{1}{{a - b}} - \frac{1}{{a - c}} + \frac{1}{{b - c}} - \frac{1}{{b - a}} + \frac{1}{{c - a}} - \frac{1}{{c - b}}\) \( = \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}} + \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}}\) \( = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\) (đpcm).
|
