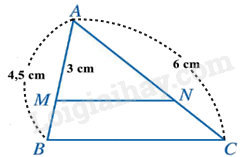
Đề thi giữa kì 2 Toán 8 - Đề số 6 - Chân trời sáng tạoPhần trắc nghiệm (2 điểm) Câu 1: Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).Đề bài
I. Trắc nghiệm
Câu 1 :
Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
Câu 2 :
Chọn phát biểu đúng.
Câu 3 :
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Câu 4 :
Cho các đường thẳng \({d_1}:y = 11x + 1;{d_2}:y = \sqrt 3 x - 7;{d_3}:y = 2x - \sqrt 2 \). Gọi \({\alpha _1},{\alpha _2},{\alpha _3}\) lần lượt là các góc tạo bởi đường thẳng \({d_1},{d_2},{d_3}\) và trục \({\rm{Ox}}\). Sắp xếp các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) theo thứ tự số đo tăng dần.
Câu 5 :
Cho hai đường thẳng \(d:y = mx - \left( {2m + 2} \right)\) và \(d':y = \left( {3 - 2m} \right)x + 1\) với \(m \ne 0\) và \(m \ne \frac{3}{2}\) Tìm giá trị của \(m\) để \(d\) và \(d\) ' cắt nhau.
Câu 6 :
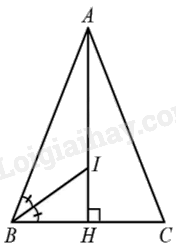
Cho hình sau với tam giác \({\rm{ABC}}\) có \(AB = AC = 9{\rm{\;cm}}\) và tia phân giác của góc \(B\) cắt đường cao \({\rm{AH}}\) ở \(I\) Biết \(\frac{{AI}}{{IH}} = \frac{3}{2}\). Tính chu vi tam giác \({\rm{ABC}}\).
Câu 7 :
Câu ca dao "Lúa chiêm lấp ló đầu bờ - Hễ nghe tiếng sấm phất cờ mà lên" về mặt khoa học được giải thích như sau: Khi trời mưa kèm theo sấm sét, nitric acid sẽ được sinh ra và hoà tan trong nước mưa, có tác dụng làm tăng cường dinh dưỡng nitrogen cho đất trồng, giúp cây lúa phát triển tươi tốt. Phân tử của nitric acid đó có một nguyên tử \({\rm{H}}\), một nguyên tử \({\rm{N}}\) và \(x\) nguyên tử \({\rm{O}}\). Xác định công thức phân tử của nitric acid đó. Biết khối lượng phân tử của nó là 63amu và khối lượng của mỗi nguyên tử \({\rm{H}},{\rm{N}},{\rm{O}}\) lần lượt là 1amu, 14amu, 16amu .
Câu 8 :
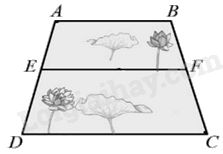
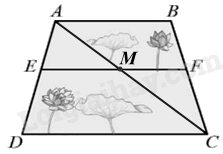
Một ao sen có dạng hình thang \(ABCD\left( {AB//CD} \right)\) với \(AB = 35{\rm{\;m}},CD = 56{\rm{\;m}}\). Người ta chọn một vị trí \(E\) ở trên bờ \({\rm{AD}}\) sao cho \(AE = \frac{3}{4}ED\) và bắc một cây cầu \({\rm{EF}}\) song song với hai bờ \(AB,CD\left( {F \in BC} \right)\). Để mọi người có thể đi trên cầu buổi tối ngắm sen, người ta căng đèn trang trí dọc theo cây cầu đó với khoảng cách giữa hai chiếc đèn liên tiếp là \(2{\rm{\;m}}\) và cả hai đầu cầu đều có đèn. Tính số tiền cần dùng để mua đèn trang trí cho cây cầu đó, biết giá mỗi chiếc đèn là 15000 đồng.
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
Đáp án : C Phương pháp giải :
Định lí Thales trong \(\Delta {\rm{ABC}},{\rm{MN}}\parallel {\rm{BC}}\) ( \({\rm{M}}\) thuộc \({\rm{AB}},{\rm{N}}\) thuộc \({\rm{AC}}\) ): \(\frac{{{\rm{AM}}}}{{{\rm{AB}}}} = \frac{{{\rm{AN}}}}{{{\rm{AC}}}};\frac{{{\rm{AM}}}}{{{\rm{MB}}}} = \frac{{{\rm{AN}}}}{{{\rm{NC}}}};\frac{{{\rm{MB}}}}{{{\rm{AB}}}} = \frac{{{\rm{NC}}}}{{{\rm{AC}}}}\) Lời giải chi tiết :
Xét tam giác \(ABC\) có \(MN\parallel BC\) nên: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (Định lí Thales) Suy ra \(\frac{3}{{4,5}} = \frac{{AN}}{6}\) hay \(AN = 6.3:4,5 = 4{\rm{\;cm}}\) Đáp án C.
Câu 2 :
Chọn phát biểu đúng.
Đáp án : D Phương pháp giải :
Khái niệm hàm số bậc nhất có dạng \(y = ax + b\), trong đó a, b là các số cho trước và \(a \ne 0\) Lời giải chi tiết :
Hàm số bậc nhất có dạng \(y = ax + b\), trong đó a, b là các số cho trước và \(a \ne 0\) Đáp án D.
Câu 3 :
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Đáp án : D Phương pháp giải :
Phương trình dạng \({\rm{ax}} + {\rm{b}} = 0\), với \({\rm{a}}\) và \({\rm{b}}\) là hai số đã cho và \({\rm{a}} \ne 0\), được gọi là phương trình bậc nhất một ân. Lời giải chi tiết :
Các phương trình \(3x + \frac{3}{5} = 0,\frac{2}{3}y - 7 = 0,7 = 2t\) có dạng nên là phương trình bậc nhất một ẩn. Phương trình \({z^2} - 9 = 0\) có bậc hai nên không là phương trình bậc nhất một ẩn Đáp án D.
Câu 4 :
Cho các đường thẳng \({d_1}:y = 11x + 1;{d_2}:y = \sqrt 3 x - 7;{d_3}:y = 2x - \sqrt 2 \). Gọi \({\alpha _1},{\alpha _2},{\alpha _3}\) lần lượt là các góc tạo bởi đường thẳng \({d_1},{d_2},{d_3}\) và trục \({\rm{Ox}}\). Sắp xếp các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) theo thứ tự số đo tăng dần.
Đáp án : A Phương pháp giải :
Hệ số góc \(a\) càng lớn thì góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \({\rm{Ox}}\) càng lớn Lời giải chi tiết :
Gọi hệ số góc của các đường thẳng \({d_1},{d_2},{d_3}\) lần lượt là \({a_1},{a_2},{a_3}\). Khi đó, ta có \({a_1} = 11,{a_2} = \sqrt 3 ,{a_3} = 2\). Mà \(\sqrt 3 < 2 < 11\), suy ra \({a_2} < {a_3} < {a_1}\). Vậy các góc được sắp xếp theo thứ tự tăng dần là: \({\alpha _2} < {\alpha _3} < {\alpha _1}\). Đáp án A.
Câu 5 :
Cho hai đường thẳng \(d:y = mx - \left( {2m + 2} \right)\) và \(d':y = \left( {3 - 2m} \right)x + 1\) với \(m \ne 0\) và \(m \ne \frac{3}{2}\) Tìm giá trị của \(m\) để \(d\) và \(d\) ' cắt nhau.
Đáp án : C Phương pháp giải :
Cho hai đường thẳng \(d:y = ax + b\left( {a \ne 0} \right)\) và \(d':y = a'x + b'\left( {a' \ne 0} \right)\) nếu \(a \ne a'\) thì \(d\) và \(d'\) cắt nhau. Lời giải chi tiết :
Để \(d\) và \(d'\) cắt nhau thì \(m \ne 3 - 2m\). Suy ra \(m \ne 1\). Vậy với \(m \ne 0,m \ne \frac{3}{2},m \ne 1\) thì \(d\) và \(d'\) cắt nhau. Đáp án C.
Câu 6 :
Cho hình sau với tam giác \({\rm{ABC}}\) có \(AB = AC = 9{\rm{\;cm}}\) và tia phân giác của góc \(B\) cắt đường cao \({\rm{AH}}\) ở \(I\) Biết \(\frac{{AI}}{{IH}} = \frac{3}{2}\). Tính chu vi tam giác \({\rm{ABC}}\).
Đáp án : C Phương pháp giải :
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. Từ đó tính được cạnh \({\rm{BH}}\). Áp dụng tính chất đường cao trong tam giác cân cũng là đường trung tuyến, tính được cạnh \({\rm{BC}}\). Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác. Lời giải chi tiết :
\(\Delta ABH\) có \(BI\) là tia phân giác của góc B suy ra \(\frac{{BA}}{{BH}} = \frac{{IA}}{{IH}} = \frac{3}{2}\) \(BH = \frac{2}{3}BA = \frac{2}{3} \cdot 9 = 6\left( {{\rm{\;cm}}} \right)\). Do \(\Delta ABC\) cân ở \(A\) nên đường cao \(AH\) cũng là đường trung tuyến. Do đó, \(HB = HC\) suy ra \(BC = 2BH = 2.6 = 12\left( {{\rm{\;cm}}} \right)\). Vậy chu vi \(\Delta ABC\) là: \(AB + AC + BC = 9 + 9 + 12 = 30\left( {{\rm{\;cm}}} \right)\). Đáp án C.
Câu 7 :
Câu ca dao "Lúa chiêm lấp ló đầu bờ - Hễ nghe tiếng sấm phất cờ mà lên" về mặt khoa học được giải thích như sau: Khi trời mưa kèm theo sấm sét, nitric acid sẽ được sinh ra và hoà tan trong nước mưa, có tác dụng làm tăng cường dinh dưỡng nitrogen cho đất trồng, giúp cây lúa phát triển tươi tốt. Phân tử của nitric acid đó có một nguyên tử \({\rm{H}}\), một nguyên tử \({\rm{N}}\) và \(x\) nguyên tử \({\rm{O}}\). Xác định công thức phân tử của nitric acid đó. Biết khối lượng phân tử của nó là 63amu và khối lượng của mỗi nguyên tử \({\rm{H}},{\rm{N}},{\rm{O}}\) lần lượt là 1amu, 14amu, 16amu .
Đáp án : D Phương pháp giải :
Giải bài toán bằng cách lập phương trình bậc nhất. Lời giải chi tiết :
Số nguyên tử \({\rm{O}}\) trong phân tử nitric acid là \(x\) (nguyên tử). Điều kiện \(x \in {\mathbb{N}^{\rm{*}}}\). Khối lượng của các nguyên tử \({\rm{O}}\) là 16x (amu) Khối lượng của nguyên tử H là 1.1=1 (amu) Khối lượng của nguyên tử N là 14.1=14 (amu) Theo giả thiết, ta có phương trình: \(16x + 14 + 1 = 63\) \(16x + 15 = 63\) \(16x = 48\) \(x = 48:16\) \(x = 3\left( {TM} \right)\) Vậy công thức phân tử của nitric acid đó là \({\rm{HN}}{{\rm{O}}_3}\). Đáp án D.
Câu 8 :
Một ao sen có dạng hình thang \(ABCD\left( {AB//CD} \right)\) với \(AB = 35{\rm{\;m}},CD = 56{\rm{\;m}}\). Người ta chọn một vị trí \(E\) ở trên bờ \({\rm{AD}}\) sao cho \(AE = \frac{3}{4}ED\) và bắc một cây cầu \({\rm{EF}}\) song song với hai bờ \(AB,CD\left( {F \in BC} \right)\). Để mọi người có thể đi trên cầu buổi tối ngắm sen, người ta căng đèn trang trí dọc theo cây cầu đó với khoảng cách giữa hai chiếc đèn liên tiếp là \(2{\rm{\;m}}\) và cả hai đầu cầu đều có đèn. Tính số tiền cần dùng để mua đèn trang trí cho cây cầu đó, biết giá mỗi chiếc đèn là 15000 đồng.
Đáp án : A Phương pháp giải :
Áp dụng hệ quả của định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. Áp dung định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ. Gọi \(M\) là giao điểm của \({\rm{AC}}\) và \({\rm{EF}}\). Chứng minh được: \(\frac{{MF}}{{AB}} = \frac{{MC}}{{AC}} = \frac{{DE}}{{DA}};\frac{{AE}}{{AD}} = \frac{{EM}}{{DC}}\) Từ đó tính được \({\rm{ME}},{\rm{MF}},{\rm{EF}}\) Tính số bóng đèn bằng \(\left( {EF:2} \right) + 1\) Tính số tiền mua bóng đèn. Lời giải chi tiết :
Gọi \(M\) là giao điểm của \({\rm{AC}}\) và \({\rm{EF}}\). Vì \(AE = \frac{3}{4}ED\) nên \(\frac{{AE}}{3} = \frac{{ED}}{4} = \frac{{AE + ED}}{{3 + 4}} = \frac{{AD}}{7}\) suy ra \(\frac{{AE}}{{AD}} = \frac{3}{7};\frac{{ED}}{{AD}} = \frac{4}{7}\) Xét \(\Delta ACD,ME//CD\) suy ra \(\frac{{AE}}{{AD}} = \frac{{EM}}{{CD}}\) (hệ quả của định lí Thales) nên \(\frac{{ME}}{{56}} = \frac{3}{7}\) hay \(ME = 24{\rm{\;m}}\). \(\frac{{MC}}{{AC}} = \frac{{DE}}{{DA}}\) (định lí Thales) (1) Xét \(\Delta ABC,MF//AB\) nên \(\frac{{MC}}{{AC}} = \frac{{MF}}{{AB}}\) (định lí Thales) (2) Từ (1), (2) suy ra \(\frac{{MF}}{{AB}} = \frac{{DE}}{{DA}}\) hay \(\frac{{MF}}{{35}} = \frac{4}{7}\) suy ra \(MF = 20{\rm{\;m}}\). Ta có \(EF = ME + MF = 24 + 20 = 44\left( {{\rm{\;m}}} \right)\). Số chiếc đèn cần dùng để trang trí dọc theo cây cầu EF là: \(\left( {44:2} \right) + 1 = 23\). Số tiền cần dùng để mua đèn trang trí cho cây cầu đó là: \(15000.23 = 345000\) (đồng). Đáp án A.
II. Tự luận
Phương pháp giải :
Giải bài toán bằng cách lập phương trình bậc nhất.
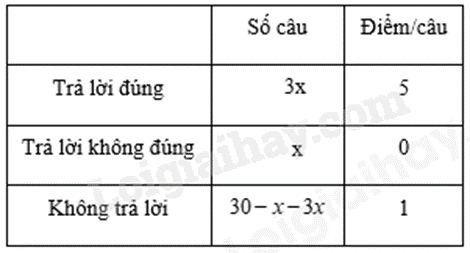
PT: tổng số điểm là 85 điểm. Lời giải chi tiết :
Gọi \(x\) là số câu trả lời không đúng \(\left( {x \in {\mathbb{N}^{\rm{*}}},x \le 30} \right)\). Số câu trả lời đúng là \(3{\rm{x}}\) Số câu không trả lời là: \(30 - x - 3x = 30 - 4x\). Vì tổng số điểm là 85 điểm nên ta có phương trình: \(5.3x + 0.x + \left( {30 - 4x} \right) = 85\) \(15x + 30 - 4x = 85\) \(15x - 4x = 85 - 30\) \(11x = 55\) \(x = 5\left( {TM} \right)\) Vậy số câu trả lời không đúng là 5 câu Số câu trả lời đúng là \(5.3 = 15\) câu Số câu không trả lời là \(30 - 5 - 15 = 10\) câu Phương pháp giải :
Phương trình bậc nhất \(ax + b = 0\left( {a \ne 0} \right)\) có nghiệm \(x = \frac{{ - b}}{a}\) Sử dụng quy tắc chuyển vế đổi dấu, quy tắc nhân hoặc chia. Lời giải chi tiết :
a) \(1,5\left( {x - 5} \right) + 11 = 7\left( {x - 8} \right) - 50,5\) \(1,5x - 7,5 + 11 = 7x - 56 - 50,5\) \(7x - 1,5x = 11 + 56 + 50,5 - 7,5\) \(5,5x = 110\) \(x = 110:5,5\) \(x = 20\) Vậy \(x = 20\) \(\frac{{6\left( {x - 4} \right)}}{{30}} + \frac{{3\left( {3x - 2} \right)}}{{30}} - \frac{{30x}}{{30}} = \frac{{10\left( {2x - 5} \right)}}{{30}} - \frac{{5\left( {7x + 2} \right)}}{{30}}\) \(6x - 24 + 9x - 6 - 30x = 20x - 50 - 35x - 10\) \( - 15x - 20 = - 15x - 60\) \( - 20 = - 60\) (vô lý) Vậy phương trình vô nghiệm. \(\frac{{4\left( {x + 1} \right)}}{{12}} - \frac{{9\left( {2x + 1} \right)}}{{12}} - \frac{{2\left( {5x + 3} \right)}}{{12}} = \frac{{12x}}{{12}} + \frac{7}{{12}}\) \(4x + 4 - 18x - 9 - 10x - 6 = 12x + 7\) \( - 24x - 11 = 12x + 7\) \(12x + 24x = - 11 - 7\) \(36x = - 18\) \(x = \frac{{ - 1}}{2}\) Vậy \(x = \frac{{ - 1}}{2}\) Phương pháp giải :
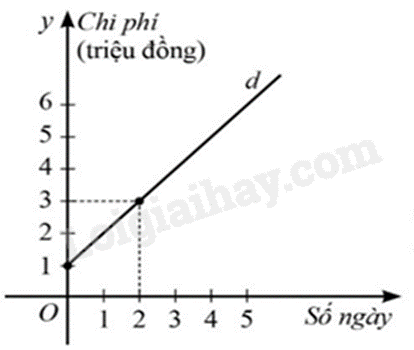
a) Dựa vào đồ thị hàm số có đường thẳng \(d\) đi qua điểm \(\left( {0;1} \right)\) và \(\left( {2;3} \right)\) Từ đó tìm hàm số bậc nhất. b) Từ đồ thị hàm số, tính chi phí khách phải trả từ 0 ngày, sau đó thực hiện yêu cầu. Lời giải chi tiết :
a) Giả sử hàm số \(y = ax + b\left( {a \ne 0} \right)\) có đồ thị của hàm số là đường thẳng \(d\) Do đường thẳng \(d\) đi qua điểm \(\left( {0;1} \right)\) nên ta có: \(1 = a.0 + b \Rightarrow b = 1\) Mặt khác, đường thẳng \(d\) cũng đi qua điểm \(\left( {2;3} \right)\) nên ta có: \(3 = a \cdot 2 + 1 \Rightarrow a = 1\) (thoả mãn). Vậy hàm số \(y = x + 1\) có đồ thị của hàm số là đường thẳng \(d\). b) Vì giao điểm của đường thẳng \(d\) với trục \({\rm{Oy}}\) tại điểm có tọa độ \(\left( {0;1} \right)\) Nên khách hành phải trả phí duy trì thẻ 1 triệu đồng trong từ 0 ngày. Tổng chi phí mà khách hàng đó phải trả khi sử dụng thẻ dịch vụ nghỉ dưỡng trên trong thời gian 4 ngày là: \(4 + 1 = 5{\rm{\;\;}}\)(triệu đồng) Phương pháp giải :
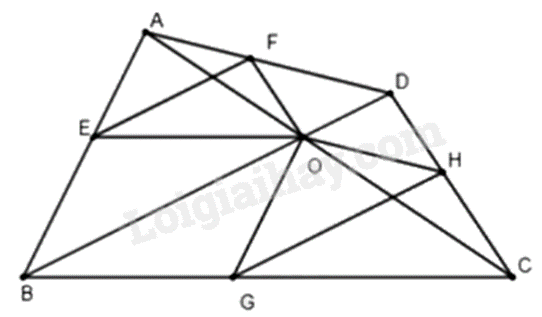
Định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ. Định lí Thales đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Lời giải chi tiết :
a) Xét \(\Delta ADC\) có \(OF//DC\), theo định lí Thales suy ra \(\frac{{AF}}{{AD}} = \frac{{AO}}{{AC}}\left( 1 \right)\) Xét \(\Delta ABC\) có \(OE//BC\), theo định lí Thales ta có \(\frac{{AE}}{{AB}} = \frac{{AO}}{{AC}}\left( 2 \right)\) Từ (1),(2) suy ra \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\) Theo định lí Thales đảo trong \(\Delta ADB\) có: \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\) suy ra \(EF//BD\left( {{\rm{dpcm}}} \right)\) b) Xét \(\Delta ADC\) có \(OH//AD\), theo định lí Thales ta có \(\frac{{CH}}{{CD}} = \frac{{CO}}{{AC}}\left( 3 \right)\) Xét \(\Delta ABC\) có \(OG//AB\), theo định lí Thales ta có \(\frac{{CG}}{{BC}} = \frac{{CO}}{{AC}}\left( 4 \right)\) Từ (3),(4) suy ra \(\frac{{CH}}{{CD}} = \frac{{CG}}{{BC}}\) Theo định lí Thales đảo suy ra \(GH//BD\). Xét \(\Delta BCD\) có \(GH//BD\), theo định lí Thales ta có \(\frac{{CH}}{{DH}} = \frac{{CG}}{{BG}}\) suy ra \(CH \cdot BG = DH \cdot CG\left( {{\rm{dpcm}}} \right)\). Phương pháp giải :
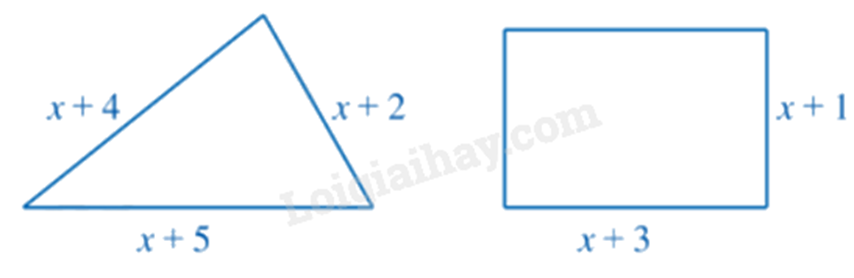
Biểu thị chu vị của hình tam giác, hình chữ nhật. Cho hai biểu thức bằng nhau, ta giải phương trình bậc nhất một ẩn: Chuyển các số hạng chứa ẩn sang một vế. Chuyển các hằng số sang vế còn lại. Lời giải chi tiết :
Chu vi tam giác là \(x + 4 + x + 2 + x + 5\) Chu vi hình chữ nhật là \(\left( {x + 3 + x + 1} \right).2\) Phương trình biểu thị sự bằng nhau của chu vi hình tam giác là: \(x + 4 + x + 2 + x + 5 = \left( {x + 3 + x + 1} \right) \cdot 2\) \(3x + 11 = \left( {2x + 4} \right) \cdot 2\) \(3x + 11 = 4x + 8\) \(4x - 3x = 11 - 8\) \(x = 3\) Vậy \(x = 3\)
|
























Danh sách bình luận