Đề thi học kì 1 Toán 8 - Đề số 1 - Chân trời sáng tạoPhần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức $4{{x}^{2}}y+6{{x}^{3}}{{y}^{2}}-10{{x}^{2}}y+4{{x}^{3}}{{y}^{2}}$ ta đượcĐề bài
I. Trắc nghiệm
Câu 1 :
Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
Câu 2 :
Giá trị của đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) tại x = y = -1 là :
Câu 3 :
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. 1. \(\frac{{14x{y^5}\left( {2x - 3y} \right)}}{{21{x^2}y{{\left( {2x - 3y} \right)}^2}}}\) 2. \(\frac{{{x^2} - \;2}}{{x{{(x - 1)}^2}}}\) + \(\frac{{2\; - \;x}}{{x{{(x - 1)}^2}}}\) 3. \(\frac{{25{x^2}}}{{17{y^4}}}\;.\;\frac{{34{y^5}}}{{15{x^3}}}\) 4. \(\frac{{{x^2} + \;8x\; + \;15}}{{{x^2} - \;9}}\) = \(\frac{{ \ldots \ldots \ldots \ldots ..}}{{x\; - \;3}}\) a. \(\frac{{10y}}{{3x}}\) b. \(\frac{{2{y^4}}}{{3x\left( {2x - 3y} \right)}}\) c. x + 5 d. \(\frac{1}{{x - 1}}\)
Câu 4 :
Tam giác ABC có đường trung tuyến AM = 2cm; cạnh BC = 4 cm. khi đó:
Câu 5 :
Một tứ giác có nhiều nhất :
Câu 6 :
Hình bình hành là một tứ giác có:
Câu 7 :
Một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài đường cao ứng với cạnh huyền là:
Câu 8 :
Cho hình chóp S.ABCD đều có thể tích bằng 100cm\(^3\), chiều cao SO bằng 12cm. Độ dài cạnh đáy của hình chóp tứ giác đó là :
Câu 9 :
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
Câu 10 :
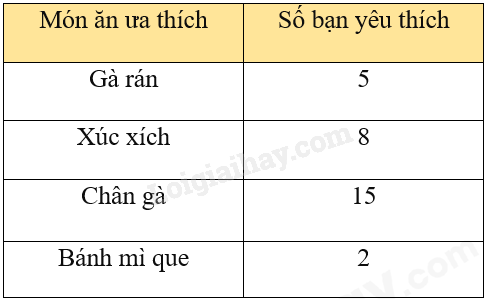
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :
Dữ liệu định lượng (số liệu) trong bảng là :
Câu 11 :
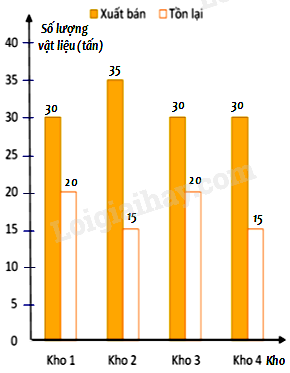
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Thu gọn đa thức \(4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\) ta được
Đáp án : D Phương pháp giải :
Sử dụng quy tắc tính với đa thức. Lời giải chi tiết :
Ta có: \(\begin{array}{l}4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}\\ = \left( {4{x^2}y - 10{x^2}y} \right) + \left( {6{x^3}{y^2} + 4{x^3}{y^2}} \right)\\ = - 6{x^2}y + 10{x^3}{y^2}\end{array}\)
Câu 2 :
Giá trị của đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) tại x = y = -1 là :
Đáp án : D Phương pháp giải :
Thay x = y = -1 vào đa thức rồi tính toán. Lời giải chi tiết :
Thay x = y = -1 vào đa thức \(xy + 2{x^2}{y^3} - {x^4}y\) ta được \(\begin{array}{l}\left( { - 1} \right).\left( { - 1} \right) + 2{\left( { - 1} \right)^2}.{\left( { - 1} \right)^3} - {\left( { - 1} \right)^4}\left( { - 1} \right)\\ = 1 - 2 + 1 = 0\end{array}\)
Câu 3 :
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. 1. \(\frac{{14x{y^5}\left( {2x - 3y} \right)}}{{21{x^2}y{{\left( {2x - 3y} \right)}^2}}}\) 2. \(\frac{{{x^2} - \;2}}{{x{{(x - 1)}^2}}}\) + \(\frac{{2\; - \;x}}{{x{{(x - 1)}^2}}}\) 3. \(\frac{{25{x^2}}}{{17{y^4}}}\;.\;\frac{{34{y^5}}}{{15{x^3}}}\) 4. \(\frac{{{x^2} + \;8x\; + \;15}}{{{x^2} - \;9}}\) = \(\frac{{ \ldots \ldots \ldots \ldots ..}}{{x\; - \;3}}\) a. \(\frac{{10y}}{{3x}}\) b. \(\frac{{2{y^4}}}{{3x\left( {2x - 3y} \right)}}\) c. x + 5 d. \(\frac{1}{{x - 1}}\) Đáp án
1. \(\frac{{14x{y^5}\left( {2x - 3y} \right)}}{{21{x^2}y{{\left( {2x - 3y} \right)}^2}}}\) b. \(\frac{{2{y^4}}}{{3x\left( {2x - 3y} \right)}}\) 2. \(\frac{{{x^2} - \;2}}{{x{{(x - 1)}^2}}}\) + \(\frac{{2\; - \;x}}{{x{{(x - 1)}^2}}}\) d. \(\frac{1}{{x - 1}}\) 3. \(\frac{{25{x^2}}}{{17{y^4}}}\;.\;\frac{{34{y^5}}}{{15{x^3}}}\) a. \(\frac{{10y}}{{3x}}\) 4. \(\frac{{{x^2} + \;8x\; + \;15}}{{{x^2} - \;9}}\) = \(\frac{{ \ldots \ldots \ldots \ldots ..}}{{x\; - \;3}}\) c. x + 5 Phương pháp giải :
Sử dụng các phép tính với phân thức đại số để tìm kết quả đúng. Lời giải chi tiết :
Đáp án: 1 – b; 2 – d; 3 – a; 4 – c.
Câu 4 :
Tam giác ABC có đường trung tuyến AM = 2cm; cạnh BC = 4 cm. khi đó:
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông. Lời giải chi tiết :
Ta có: AM = 2cm; BC = 4cm \( \Rightarrow AM = \frac{1}{2}BC\). Mà AM là đường trung tuyến ứng với cạnh BC nên AM là đường trung tuyến ứng với cạnh huyền BC hay tam giác ABC vuông tại A.
Câu 5 :
Một tứ giác có nhiều nhất :
Đáp án : C Phương pháp giải :
Áp dụng định lí tổng các góc của một tứ giác bằng \(360^0\). Lời giải chi tiết :
- Nếu 4 góc trong tứ giác đều nhọn (nhỏ hơn \(90^0\)) => Tổng 4 góc < \(4.90^0\) = \(360^0\) => Vô lí vì tổng 4 góc trong tứ giác bằng \(360^0\). - Nếu có 3 góc nhỏ hơn \(90^0\) ; 1 góc > \(90^0\) => Tổng 3 góc đó < 3.\(90^0\) = \(270^0\) => góc còn lại lớn hơn \(360^0- 270^0 = 90^0\) (thỏa mãn) Vậy tứ giác có thể có nhiều nhất 3 góc nhọn.
Câu 6 :
Hình bình hành là một tứ giác có:
Đáp án : C Phương pháp giải :
Ta sử dụng kiến thức về hình bình hành. Lời giải chi tiết :
Hình bình hành là một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C đúng.
Câu 7 :
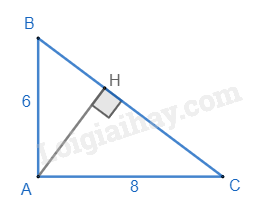
Một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài đường cao ứng với cạnh huyền là:
Đáp án : C Phương pháp giải :
Sử dụng định lí Pythagore và công thức tính diện tích tam giác. Lời giải chi tiết :
Giả sử tam giác ABC là tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài cạnh huyền BC là: \(BC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{6^2} + {8^2}} = 10\) (cm). Theo công thức tính diện tích tam giác, ta có: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\) => AB.AC = AH.BC 6.8 = AH.10 48 = AH.10 AH = 48:10 = 4,8 (cm).
Câu 8 :
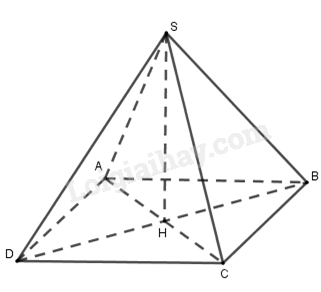
Cho hình chóp S.ABCD đều có thể tích bằng 100cm\(^3\), chiều cao SO bằng 12cm. Độ dài cạnh đáy của hình chóp tứ giác đó là :
Đáp án : B Phương pháp giải :
Dựa vào công thức tính thể tích hình chóp tứ giác để tính độ dài cạnh đáy của hình chóp đó. \(V = \frac{1}{3}{S_d}.h \) suy ra \( {S_d} = \frac{{3V}}{h}\) Lời giải chi tiết :
Xét hình chóp tứ giác đều S.ABCD có V = 100cm3, đường cao SH = 12cm. Ta có \(V = \frac{1}{3}{S_d}.h \) suy ra \( {S_d} = \frac{{3V}}{h}\) \({S_d} = \frac{{3.100}}{{12}} = 25\). Vì đáy hình chóp là hình vuông nên độ dài cạnh đáy là \(\sqrt {25} = 5\left( {cm} \right)\).
Câu 9 :
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
Đáp án : C Phương pháp giải :
Dựa vào công thức tính diện tích xung quanh của hình chóp tam giác đều \(S_{xq} = pd\) trong đó p là nửa chu vi đáy, d là trung đoạn. Lời giải chi tiết :
Nửa chu vi đáy là: p = \(\frac{{5 + 5 + 5}}{2} = 7,5\) (cm) Diện tích xung quanh của hình chóp tam giác đều đó là: \({S_{xq}} = p.d = 7,5.6 = 45\) (cm\(^2\)).
Câu 10 :
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :
Dữ liệu định lượng (số liệu) trong bảng là :
Đáp án : B Phương pháp giải :
Dựa vào phân loại dữ liệu: Dữ liệu được chia thành hai loại: Dữ liệu định tính (dữ liệu không phải số) và dữ liệu định lượng (số liệu). Lời giải chi tiết :
Dữ liệu định lượng (số liệu) trong bảng trên là dữ liệu Số bạn yêu thích : 5; 8; 15; 2.
Câu 11 :
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?
Đáp án : D Phương pháp giải :
Kiểm tra xem dữ liệu trong biểu đồ có cột nào chưa chính xác. Lời giải chi tiết :
Vì mỗi kho hàng đều có 50 tấn hàng nên tổng số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại phải bằng 50 tấn. Mà cột kho 4, số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại là: 30 + 15 = 45 (tấn) nên số liệu ở kho 4 không đúng.
II. Tự luận
Phương pháp giải :
a) Sử dụng các phương pháp phân tích đa thức thành nhân tử để rút gọn biểu thức. Thay x = 5 và y = 3 vào biểu thức để tính giá trị của biểu thức. b) Sử dụng các phương pháp phân tích đa thức thành nhân tử. Lời giải chi tiết :
a) \(\frac{{{x^2} + 3xy + \;2{y^2}}}{{{x^3} + \;2{x^2}y - \;x{y^2} - \;2{y^3}}}\) \(\begin{array}{l} = \frac{{{x^2} + xy + 2xy + 2{y^2}}}{{{x^3} + 2{x^2}y - x{y^2} - 2{y^3}}}\\ = \frac{{x\left( {x + y} \right) + 2y\left( {x + y} \right)}}{{{x^2}\left( {x + 2y} \right) - {y^2}\left( {x - 2y} \right)}}\\ = \frac{{\left( {x + 2y} \right)\left( {x + y} \right)}}{{\left( {{x^2} - {y^2}} \right)\left( {x + 2y} \right)}}\\ = \frac{{x + y}}{{\left( {x - y} \right)\left( {x + y} \right)}}\\ = \frac{1}{{x - y}}\end{array}\) Điều kiện để \(\frac{1}{{x - y}}\) xác định là \(x - y \ne 0 \Leftrightarrow x \ne y\). Tại x = 5 và y = 3 (thỏa mãn điều kiện) thì giá trị của biểu thức \(\frac{1}{{x - y}}\) là: \(\frac{1}{{5 - 3}} = \frac{1}{2}\). Vậy tại x = 5 và y = 3 thì giá trị của biểu thức \(\frac{{{x^2} + 3xy + \;2{y^2}}}{{{x^3} + \;2{x^2}y - \;x{y^2} - \;2{y^3}}}\) là \(\frac{1}{2}\). b) Phân tích \(2x - 2y - {x^2} + 2xy - {y^2}\)thành nhân tử, ta được: \(\begin{array}{l}2x - 2y - {x^2} + 2xy - {y^2}\\ = \left( {2x - 2y} \right) - \left( {{x^2} - 2xy + {y^2}} \right)\\ = 2\left( {x - y} \right) - {\left( {x - y} \right)^2}\\ = \left( {x - y} \right)\left( {2 - x + y} \right)\end{array}\) Phương pháp giải :
a) Sử dụng các phương pháp phân tích đa thức thành nhân tử để rút gọn biểu thức. b) Để A là số nguyên thì mẫu thức phải là ước của tử thức. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}\frac{{{x^2} + \;4x\; + \;4}}{{{x^3} + \;2{x^2} - 4x - 8}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{{x^2}\left( {x + 2} \right) - 4\left( {x + 2} \right)}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {{x^2} - 4} \right)\left( {x + 2} \right)}}\\ = \frac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \frac{1}{{x - 2}}\end{array}\) b) Để A là số nguyên thì \(\frac{1}{{x - 2}} \in \mathbb{Z}\) thì \(x - 2 \in \) Ư(1) \( \Rightarrow x - 2 \in \left\{ { \pm 1} \right\}\). Ta có: x – 2 = 1 \( \Rightarrow \) x = 3 (thỏa mãn điều kiện) x – 2 = -1 \( \Rightarrow \) x = 1 (thỏa mãn điều kiện) Vậy A là số nguyên khi \(x \in \left\{ {1;3} \right\}\). Phương pháp giải :
a) Dựa vào dữ liệu đề bài cho để điền vào bảng. b) Điền số tương ứng vào biểu đồ. Lời giải chi tiết :
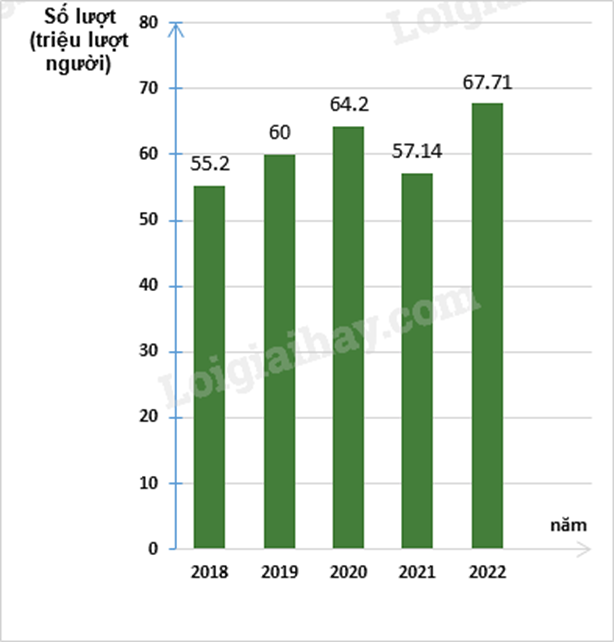
a) Ta có bảng thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm:
b) Biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên là: Phương pháp giải :
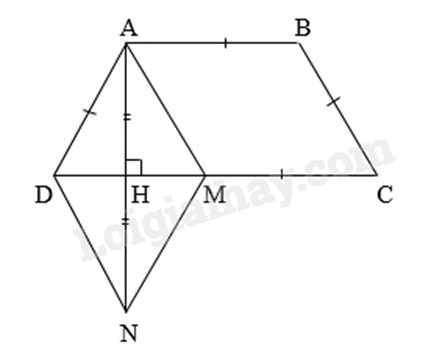
1. Sử dụng định lí Pythagore. 2. a) Chứng minh tứ giác ABCM có cặp cạnh song song và bằng nhau. b) Chứng minh AMND là hình bình hành có một góc vuông. c) Khi tứ giác AMND là hình vuông suy ra các góc tương ứng để tính số đo góc ABC. Lời giải chi tiết :
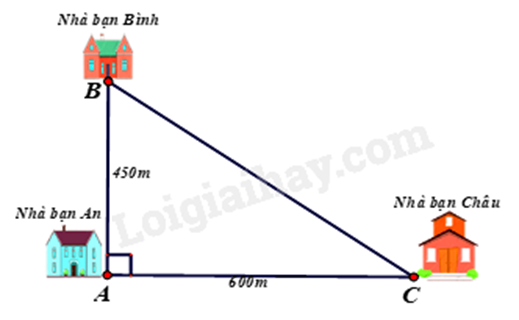
1. Xét tam giác ABC vuông tại A, ta có BC2 = AB2 + AC2 (Định lí Pythagore) BC2 = 4502 + 6002 BC2 = 562500 => BC = 750m Khoảng cách từ thành phố B đến trạm phát sóng là 750 m 2.
a) Ta có: AB = CM (\( = \frac{1}{2}\)CD) và AB // CM (M \( \in \) CD) nên ABCM là hình bình hành. (đpcm) b) Ta có AM = BC (ABCM là hình bình hành) Mà AD = BC (ABCD là hình thang cân) => AM = AD. (1) Xét tam giác ADH và NDH có: \(\left\{ \begin{array}{l}AH = NH\\\widehat {AHD} = \widehat {NHD} = {90^0}\\DH\,chung\end{array} \right. \Rightarrow \Delta ADH = \Delta NDH(c.g.c)\) \( \Rightarrow AD = DN\) (hai cạnh tương ứng). (2) Tương tự, ta chứng minh được AM = MN. (3) Từ (1), (2) và (3) suy ra AM = MN = DN = AD => tứ giác AMND là hình thoi. (đpcm) c) Khi AMND là hình vuông thì \(\widehat {ADN} = {90^0}\). Trong hình vuông AMND, đường chéo DM là tia phân giác của góc ADN nên \(\widehat {ADM} = \widehat {MDN} = \frac{{{{90}^0}}}{2} = {45^0}\). Góc BAD và góc ADC là hai góc kề một cạnh bên của hình thang ABCD nên \(\widehat {BAD} + \widehat {ADC} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {45^0} = {135^0}\). Mà ABCD là hình thang cân nên \(\widehat {BAD} = \widehat {ABC} = {135^0}\). (đpcm) Phương pháp giải :
Dựa vào hằng đẳng thức \({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\); \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\) để tìm x, y. Thay x, y vào biểu thức M để tính giá trị của biểu thức M. Lời giải chi tiết :
Ta có: \(\begin{array}{l}5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0\\\left( {4{x^2} + 8xy + 4{y^2}} \right) + ({x^2} - 2x + 1) + ({y^2} + 2y + 1) = 0\\4{\left( {x + y} \right)^2} + {\left( {x-1} \right)^2} + {(y + 1)^2} = 0\left( * \right)\end{array}\) Vì \(4{\left( {x + y} \right)^2} \ge 0;{\left( {x-1} \right)^2} \ge 0;{(y + 1)^2} \ge \;0\) với mọi x, y Nên (*) xảy ra khi \(\left\{ \begin{array}{l}x + y = 0\\x - 1 = 0\\y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - y\\x = 1\\y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\). Thay x = 1 và y = -1 vào biểu thức M, ta được: \(M = {(1 - 1)^{2017}} + {(1 - 2)^{2018}} + {( - 1 + 1)^{2019}} = {\left( { - 1} \right)^{2018}} = 1\) . Vậy M = 1 .
|














 b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.
b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.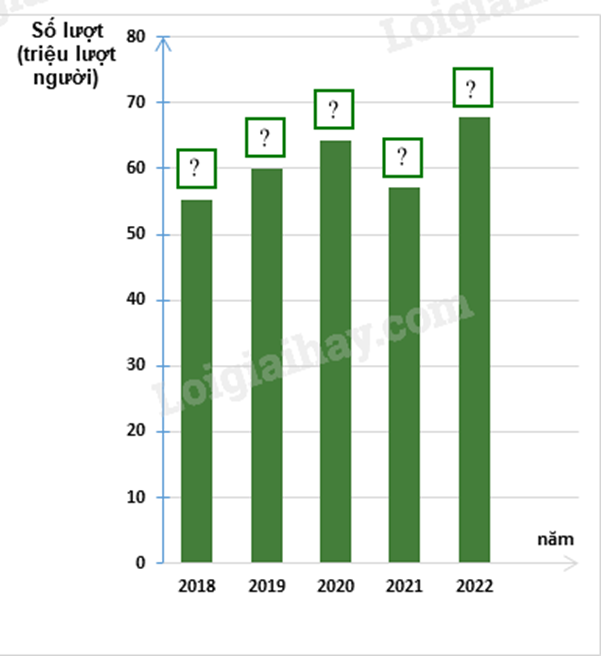










Danh sách bình luận