Đề thi học kì 2 Toán 8 - Đề số 1 - Chân trời sáng tạoPhần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?Đề bài
I. Trắc nghiệm
Câu 1 :
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Câu 2 :
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
Câu 3 :
Phương trình \(4x - 2 = 0\) có nghiệm là
Câu 4 :
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
Câu 5 :
Trên bàn có một tấm bìa hình tròn được chia thành 8 hình quạt bằng nhau và được đánh số từ 1 đển 8. Xoay tấm bìa xung quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Có bao nhiêu kết quả thuận lợi cho biến cố "Mũi tên chỉ vào ô ghi số chẵn"?
Câu 6 :
Một hộp chứa 16 tấm thẻ cùng loại được đánh số từ 11 đến 26. An lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 4 là
Câu 7 :
Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 500 chiếc laptop được sản xuất và thấy có 6 chiếc bị lỗi. Trong một lô hàng có 1200 chiếc laptop. Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop bị lỗi.
Câu 8 :
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
Câu 9 :
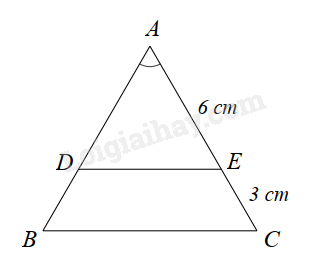
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân. Chọn kết luận đúng trong các câu sau:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đáp án : B Phương pháp giải :
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\). Lời giải chi tiết :
Phương trình \(2x - 5 = 0\) có dạng \(ax + b = 0\) với \(a = 2\) nên ta chọn đáp án B. Đáp án B.
Câu 2 :
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
Đáp án : B Phương pháp giải :
Thay m vào phương trình, đưa phương trình về dạng ax + b = 0 để giải. Lời giải chi tiết :
Thay \(m = - 1\) vào phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\), ta có: \(\begin{array}{l}\left[ {2{{\left( { - 1} \right)}^2} - 2} \right]x = - 1 + 1\\\left( {2 - 2} \right)x = 0\end{array}\) \(0.x = 0\) (luôn đúng). Vậy phương trình có vô số nghiệm. Đáp án B.
Câu 3 :
Phương trình \(4x - 2 = 0\) có nghiệm là
Đáp án : D Phương pháp giải :
Giải phương trình có dạng \(ax + b = 0\). Lời giải chi tiết :
Ta có: \(\begin{array}{l}4x - 2 = 0\\4x = 2\\x = \frac{1}{2}\end{array}\) Đáp án D.
Câu 4 :
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
Đáp án : C Phương pháp giải :
Coi bể nước bằng 1. Tính số phần bể mà vòi chảy được trong 1 giờ. Lời giải chi tiết :
Coi bể nước là 1. Vì vòi nước chảy đầy bể trong 5 giờ nên trong 1 giờ vòi chảy được là: \(1:5 = \frac{1}{5}\) (bể) Đáp án C.
Câu 5 :
Trên bàn có một tấm bìa hình tròn được chia thành 8 hình quạt bằng nhau và được đánh số từ 1 đển 8. Xoay tấm bìa xung quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Có bao nhiêu kết quả thuận lợi cho biến cố "Mũi tên chỉ vào ô ghi số chẵn"?
Đáp án : B Phương pháp giải :
Xác định các kết quả thuận lợi cho biến cố. Lời giải chi tiết :
Có 4 kết quả thuận lợi cho biến cố “Mũi tên chỉ vào ô ghi số chẵn”, đó là: 2; 4; 6; 8. Đáp án B.
Câu 6 :
Một hộp chứa 16 tấm thẻ cùng loại được đánh số từ 11 đến 26. An lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 4 là
Đáp án : C Phương pháp giải :
Xác định tổng số kết quả có thể và số kết quả thuận lợi cho biến cố Tính tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể. Lời giải chi tiết :
Hộp chứa 16 tấm thẻ nên có 16 kết quả có thể khi lấy ngẫu nhiên một thẻ từ hộp. Có 4 số chia hết cho 4 từ 11 đến 26, đó là 12, 16, 20, 24. Do đó có 4 kết quả thuận lợi cho biến cố thẻ chọn ra ghi số chia hết cho 4. Vậy xác suất để thẻ chọn ra ghi số chia hết cho 4 là: \(\frac{4}{{16}} = \frac{1}{4}\). Đáp án C.
Câu 7 :
Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 500 chiếc laptop được sản xuất và thấy có 6 chiếc bị lỗi. Trong một lô hàng có 1200 chiếc laptop. Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop bị lỗi.
Đáp án : C Phương pháp giải :
Tính xác suất laptop lỗi, từ đó suy ra với 1200 chiếc laptop có khoảng bao nhiêu chiếc laptop lỗi. Lời giải chi tiết :
Xác suất laptop lỗi là: \(\frac{6}{{500}} = \frac{3}{{250}}\) Do đó trong lô hàng có 1200 chiếc laptop thì có khoảng \(1200.\frac{3}{{250}} = \frac{{72}}{5} \approx 14\) chiếc bị lỗi. Đáp án C.
Câu 8 :
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
Đáp án : B Phương pháp giải :
Xác định tỉ số giữa các cạnh tương ứng của hai tam giác. Lời giải chi tiết :
$\Delta ABC\backsim \Delta DEF$ nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = k\). Vậy \(k = \frac{{AC}}{{DF}}\). Đáp án B.
Câu 9 :
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân. Chọn kết luận đúng trong các câu sau:
Đáp án : C Phương pháp giải :
Chứng minh $\Delta ADE\backsim \Delta ABC$ theo trường hợp cạnh – góc – cạnh. Lời giải chi tiết :
Vì \(\Delta ABC,\Delta ADE\) cân nên \(AB = AC\); \(AD = AE\left( { = 6cm} \right)\). Xét \(\Delta ABC\) và \(\Delta ADE\) có: \(\widehat A\) chung \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\) (vì \(AB = AC;AD = AE\)) suy ra $\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$ suy ra \(k = \frac{{AC}}{{AE}} = \frac{{AE + EC}}{{AE}} = \frac{{6 + 3}}{6} = \frac{9}{6} = \frac{3}{2}\). Đáp án C.
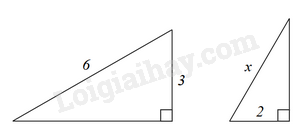
Đáp án : B Phương pháp giải :
Dựa vào các trường hợp đồng dạng của hai tam giác để tìm x. Lời giải chi tiết :
Để hai tam giác đồng dạng thì \(\frac{2}{3} = \frac{x}{6}\) suy ra \(x = \frac{2}{3}.6 = 4\). Đáp án B.
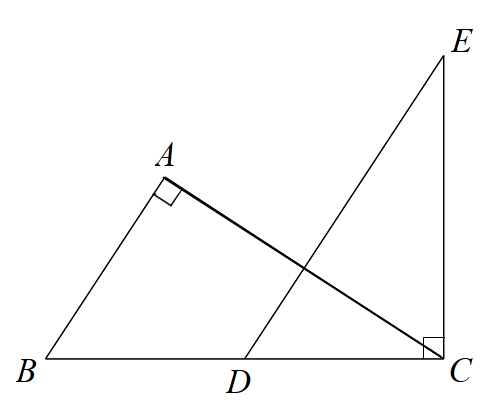
Đáp án : D Phương pháp giải :
Dựa vào AB // DE suy ra \(\widehat {ABC} = \widehat {EDC}\). Chứng minh $\Delta ABC\backsim \Delta CDE\left( g.g \right)$ suy ra tỉ số giữa các cặp cạnh tương ứng. Lời giải chi tiết :
Vì AB // DE nên \(\widehat {ABC} = \widehat {EDC}\) (hai góc đồng vị) Xẻ \(\Delta ABC\) và \(\Delta CDE\) có: \(\widehat A = \widehat C\left( { = {{90}^0}} \right)\) \(\widehat {ABC} = \widehat {EDC}\) (cmt) Suy ra $\Delta ABC\backsim \Delta CDE\left( g.g \right)$. Từ đó ta được: \(\frac{{AB}}{{AC}} = \frac{{CD}}{{CE}}\) suy ra \(AB.CE = AC.CD\). (A đúng) \(\frac{{AB}}{{BC}} = \frac{{CD}}{{DE}}\) suy ra \(AB.DE = BC.CD\) (B đúng) \(\frac{{AC}}{{BC}} = \frac{{CE}}{{DE}}\) suy ra \(AC.DE = CE.BC\) (C đúng) Vậy D sai (vì không có tỉ lệ nào suy ra \(AB.AC = DE.DC\)). Đáp án D.
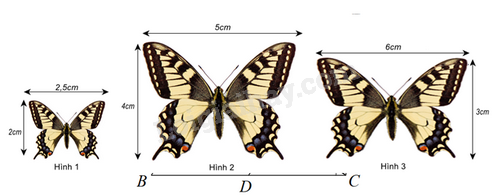
Đáp án : A Phương pháp giải :
Kiểm tra tỉ số các cặp cạnh của các hình trên. Lời giải chi tiết :
Ta có: \(\frac{2}{{2,5}} = \frac{4}{5} \ne \frac{3}{6}\) nên hình 1 và hình 2 là hai hình đồng dạng Đáp án A.
II. Tự luận
Phương pháp giải :
Đưa phương trình về dạng ax + b = 0 để giải. Lời giải chi tiết :
a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\) \(\begin{array}{l}\frac{2}{3}x + \frac{5}{2} = 0\\\frac{2}{3}x = - \frac{5}{2}\\x = - \frac{5}{2}:\frac{2}{3}\\x = - \frac{{15}}{4}\end{array}\) Vậy nghiệm của phương trình là \(x = - \frac{{15}}{4}\). b) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x\) \(\begin{array}{l}\frac{{5\left( {7x - 1} \right)}}{{5.6}} = \frac{{6\left( {16 - x} \right)}}{{6.5}} - \frac{{30.2x}}{{30}}\\5\left( {7x - 1} \right) = 6\left( {16 - x} \right) - 60x\\35x - 5 = 96 - 6x - 60x\\35x + 6x + 60x = 96 + 5\\101x = 101\\x = 1\end{array}\) Vậy nghiệm của phương trình là \(x = 1\) Phương pháp giải :
Giải bài toán bằng cách lập phương trình. Gọi quãng đường AB là x (km) (x > 0). Biểu diễn thời gian xe tải, xe con đi theo x và lập phương trình. Giải phương trình và kiểm tra nghiệm. Lời giải chi tiết :
Gọi quãng đường AB dài x (km) (x > 0). Thời gian xe tải đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ). \(\frac{3}{4}\) quãng đường AB là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô con đi hết \(\frac{3}{4}\) quãng đường AB là: \(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ) Vận tốc xe con sau khi tăng thêm 5km/h là: 45 + 5 = 50 (km/h) Quãng đường còn lại là: \(1 - \frac{3}{4}x = \frac{x}{4}\) (km) Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường AB là: \(\frac{x}{4}:50 = \frac{x}{{200}}\) (h) Vì xe con đến B sớm hơn xe tải là 2 giờ 27 phút = \(\frac{{49}}{{20}}\)h nên ta có phương trình: \(\begin{array}{l}\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\\\frac{{20x}}{{600}} - \frac{{10x}}{{600}} - \frac{{3x}}{{600}} = \frac{{1470}}{{600}}\\\frac{{7x}}{{600}} = \frac{{1470}}{{600}}\\7x = 1470\\x = 210(TM)\end{array}\) Vậy quãng đường AB dài 210km. Phương pháp giải :
Biến đổi tương đương đưa phương trình về dạng ax = b: + Nếu a = 0 và b ≠ 0 thì phương trình vô nghiệm. + Nếu a ≠ 0 thì phương trình có nghiệm duy nhất \(x = \frac{b}{a}\). Lời giải chi tiết :
Ta có: \(2\left( {x - 1} \right) - mx = 3\) \(\begin{array}{l}2x - 2 - mx = 3\\2x - mx = 3 + 2\\(2 - m)x = 5\end{array}\) a) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) vô nghiệm thì: \(2 - m = 0\) suy ra \(m = 2\). Vậy khi m = 2 thì phương trình vô nghiệm. b) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) có nghiệm duy nhất thì: \(2 - m \ne 0\) suy ra \(m \ne 2\). Vậy khi \(m \ne 2\) thì phương trình có nghiệm duy nhất \(x = \frac{5}{{2 - m}}\). Phương pháp giải :
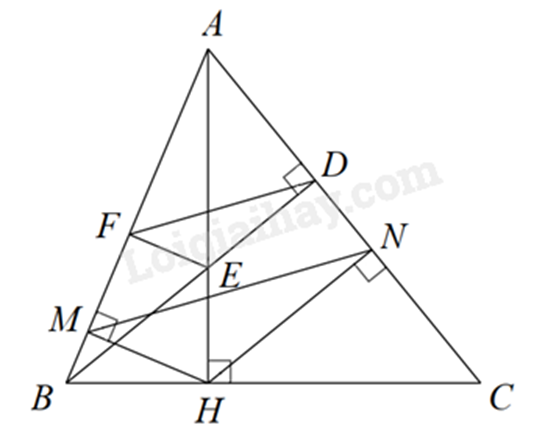
a) Chứng minh $\Delta AMH\backsim \Delta AHB\left( g.g \right)$ b) Chứng minh $\Delta ANH\backsim \Delta AHC\left( g.g \right)$ suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\). c) Áp dụng định lý Thales để chứng minh \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\left( { = \frac{{AD}}{{AN}}} \right)\) Chứng minh $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ suy ra \(\widehat {AEF} = \widehat {AHM}\) mà \(\widehat {AHM} = \widehat {ABC}\) nên \(\widehat {AEF} = \widehat {ABC}\). Lời giải chi tiết :
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có: \(\widehat {AMH} = \widehat {AHB}\left( { = {{90}^0}} \right)\) \(\widehat A\) chung suy ra $\Delta AMH\backsim \Delta AHB\left( g.g \right)$ (đpcm) b) Xét \(\Delta ANH\) và \(\Delta AHC\) có: \(\widehat {ANH} = \widehat {AHC}\left( { = {{90}^0}} \right)\) \(\widehat A\) chung suy ra $\Delta ANH\backsim \Delta AHC\left( g.g \right)$ suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\) (đpcm) c) Vì DF // NM nên \(\frac{{AF}}{{AM}} = \frac{{AD}}{{AN}}\) Vì DE // HN nên \(\frac{{AE}}{{AH}} = \frac{{AD}}{{AN}}\) suy ra \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\) Xét \(\Delta AFE\) và \(\Delta AMH\) có: \(\widehat A\) chung \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\) suy ra $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ nên \(\widehat {AEF} = \widehat {AHM}\) Mà \(\widehat {AHM} = \widehat {ABC}\)(vì $\Delta AMH\backsim \Delta AHB$) Do đó \(\widehat {AEF} = \widehat {ABC}\) (đpcm) Phương pháp giải :
Tính xác suất thực nghiệm của biến cố “Lấy được viên bi màu xanh”. Gọi số bi trong túi là x (x > 9). Vì số lần thử lớn nên xác suất thực nghiệm gần bằng xác suất của biến cố “Lấy được viên bi màu xanh”. Do đó ta tính được số viên bi trong hộp, suy ra số viên bi đỏ. Lời giải chi tiết :
Vì lặp lại phép thử 100 lần, Nam thấy có 40 lần lấy được viên bi đỏ nên số lần lấy được viên bi xanh là: 100 – 40 = 60 (lần). Do đó xác suất thực nghiệm của biến cố "Lấy được viên bi màu xanh" là: \(\frac{{60}}{{100}} = \frac{3}{5} = 0.6\) Gọi số bi trong túi là x (x > 9). Vì số lần thử lớn nên xác suất thực nghiệm gần bằng xác suất của biến cố “Lấy được viên bi màu xanh”, do đó: \(\frac{9}{x} \approx 0,6\) suy ra \(x \approx 15\) (viên bi) Vậy trong hộp có khoảng 15 – 9 = 6 viên bi màu đỏ.
|