Đề kiểm tra giữa kì 1 Toán 5 - Đề số 6Tải về Chữ số 3 trong số 21,753 có giá trị là .... 0,408km2 = ……. ha. Số thích hợp để viết vào chỗ chấm là .... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài I. TRẮC NGHIỆM (Khoanh vào chữ đặt trước câu trả lời đúng) Câu 1: Chữ số 3 trong số 21,753 có giá trị là: A. 3 B. $\frac{3}{{10}}$ C. $\frac{3}{{100}}$ D. $\frac{3}{{1000}}$ Câu 2: Số tự nhiên không nằm giữa 2,65 và 5,12 là: A. 2 B. 3 C. 4 D. 5 Câu 3: Dãy số thập phân nào dưới đây được viết theo thứ tự từ bé đến lớn? A. 0,42; 0,024; 0,042; 0,24; 0,204 B. 0,024; 0,042; 0,24; 0,204; 0,402 C. 0,024; 0,042; 0,24; 0,204; 0,42 D. 0,024; 0,042; 0,204; 0,24; 0,402 Câu 4: 0,408km2 = ……. ha. Số thích hợp để viết vào chỗ chấm là: A. 408 B. 40,8 C. 4,08 D. 4,008 Câu 5: 3 tấn 5kg = … tạ. Số thích hợp để viết vào chỗ chấm là: A. 3,5 B. 30,5 C. 3,005 D. 30,05 Câu 6: Mẹ cho hai anh em 40 cái kẹo. Số kẹo của em gấp rưỡi số kẹo của anh. Mẹ cho em số kẹo là: A. 20 cái B. 24 cái C. 30 cái D. 32 cái Câu 7: Số thích hợp để viết vào chỗ chấm để được $\frac{{18}}{{54}}$ = $\frac{{...}}{9}$ là: A. 2 B. 18 C. 3 D. 6 Câu 8: Một ô tô đi trong 5 giờ được 225 km. Ô tô đó đi trong 8 giờ được quãng đường là: A. 360km B. 345km C. 320km D. 400km II. TỰ LUẬN Câu 9: Tính: a) ${\mkern 1mu} 3 \times \frac{1}{2} + \frac{1}{4} \times \frac{1}{3}$ b) ${\mkern 1mu} 1\frac{4}{5} - \frac{2}{3}:2\frac{1}{3}$ Câu 10: Điền dấu (>, <, =) a) 5 ha 89m2 … 5,089 ha b) 8ha 6dam2 … 8$\frac{5}{{100}}$ ha c) 18, 064cm … 18 m 64 cm d) 750 kg … $\frac{3}{5}$ tấn Câu 11: Một thửa ruộng hình chữ nhật có chu vi 240 m và chiều dài gấp 3 lần chiều rộng. a) Tính diện tích của thửa ruộng. b) Người ta cấy lúa trên thửa ruộng, biết rằng cứ 100m2 thu được 50 kg thóc. Hỏi cả thửa ruộng đó thu hoạch được bao nhiêu tạ thóc? Câu 12: Tính: $\frac{1}{{1 \times 2}} + \frac{1}{{2 \times 3}} + \frac{1}{{3 \times 4}} + \frac{1}{{4 \times 5}} + ... + \frac{1}{{99 \times 100}}$. Đáp án HƯỚNG DẪN GIẢI CHI TIẾT I. TRẮC NGHIỆM
Câu 1: Chữ số 3 trong số 21,753 có giá trị là: A. 3 B. $\frac{3}{{10}}$ C. $\frac{3}{{100}}$ D. $\frac{3}{{1000}}$ Phương pháp: Chữ số 3 trong số 21, 753 có giá trị là $\frac{3}{{1000}}$. Cách giải: Chữ số 3 trong số 21, 753 có giá trị là $\frac{3}{{1000}}$. Chọn D. Câu 2: Số tự nhiên không nằm giữa 2,65 và 5,12 là: A. 2 B. 3 C. 4 D. 5 Phương pháp: Số tự nhiên không nằm giữa 2,65 và 5,12 là: 2. Cách giải: Số tự nhiên không nằm giữa 2,65 và 5,12 là: 2. Chọn A. Câu 3: Dãy số thập phân nào dưới đây được viết theo thứ tự từ bé đến lớn? A. 0,42; 0,024; 0,042; 0,24; 0,204 B. 0,024; 0,042; 0,24; 0,204; 0,402 C. 0,024; 0,042; 0,24; 0,204; 0,42 D. 0,024; 0,042; 0,204; 0,24; 0,402 Phương pháp: So sánh các số thập phân có trong dãy rồi sắp xếp chúng theo thứ tự tăng dần. Cách giải: Dãy số thập phân nào dưới đây được viết theo thứ tự từ bé đến lớn là: 0,024; 0,042; 0,204; 0,24; 0,402. Chọn D. Câu 4: 0,408km2 = ……ha. Số thích hợp để viết vào chỗ chấm là: A. 408 B. 40,8 C. 4,08 D. 4,008 Phương pháp: Ta có: $1k{m^2} = 100{\mkern 1mu} ha$. Vậy để đổi từ $k{m^2}$ sang ha ta nhân số đó với 100. Cách giải: Ta có: 0,408km2 = 40,8 ha Chọn B. Câu 5: 3 tấn 5kg = … tạ. Số thích hợp để viết vào chỗ chấm là: A. 3,5 B. 30,5 C. 3,005 D. 30,05 Phương pháp: Đổi 3 tấn sang đơn vị tạ, rồi đổi 5 kg sang tạ rồi cộng chúng lại với nhau. Cách giải: 3 tấn = 30 tạ 5 kg =$\frac{5}{{100}}$ tạ = 0,05 tạ. Vậy 3 tấn 5kg = 30,05 tạ. Chọn D. Câu 6: Mẹ cho hai anh em 40 cái kẹo. Số kẹo của em gấp rưỡi số kẹo của anh. Mẹ cho em số kẹo là: A. 20 cái B. 24 cái C. 30 cái D. 32 cái Phương pháp: Tìm hai số khi biết tổng và tỉ của hai số đó để tìm ra số kẹo mà mẹ đã cho em. Cách giải: Tổng số kẹo của hai anh em là 40 cái kẹo. Số kẹo của em gấp rưỡi số kẹo của anh hay nói cách khác là số kẹo của em bằng $\frac{3}{2}$ số kẹo của anh. Coi số kẹo của em là 3 phần thì số kẹo của anh là 2 phần như thế. Tổng số phần bằng nhau là: 3 + 2 = 5 (phần) Số kẹo của em là: 40 : 5 x 3 = 24 (cái kẹo) Đáp số: 24 cái kẹo. Chọn B. Câu 7: Số thích hợp để viết vào chỗ chấm để được $\frac{{18}}{{54}}$ = $\frac{{...}}{9}$ là: A. 2 B. 18 C. 3 D. 6 Phương pháp: Chia cả tử số và mẫu số của phân số thứ nhất cho 6. Cách giải: Ta có: $\frac{{18}}{{54}} = \frac{3}{9}$ Vậy số thích hợp điền vào chỗ chấm là: 3. Chọn C. Câu 8: Một ô tô đi trong 5 giờ được 225 km. Ô tô đó đi trong 8 giờ được quãng đường là: A. 360km B. 345km C. 320km D. 400km Phương pháp: Tìm số ki-lô-mét ô tô đó đi trong 1 giờ, sau đó nhân với 8. Cách giải: Trong 1 giờ ô tô đó đi được số ki-lô-mét là: 225 : 5 = 45 (km) Trong 8 giờ ô tô đó đi được số ki-lô-mét là: 45 x 8 = 360 (km) Đáp số: 360 km Chọn A. II. TỰ LUẬN Câu 9: Tính: a) ${\mkern 1mu} 3 \times \frac{1}{2} + \frac{1}{4} \times \frac{1}{3}$ b) ${\mkern 1mu} 1\frac{4}{5} - \frac{2}{3}:2\frac{1}{3}$ Phương pháp: Thực hiện phép tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau. Cách giải:
Câu 10: Điền dấu (>, <, =) a) 5 ha 89m2 … 5,089 ha b) 8ha 6dam2 … 8$\frac{5}{{100}}$ ha c) 18, 064cm … 18 m 64 cm d) 750 kg … $\frac{3}{5}$ tấn Phương pháp: Đổi các đơn vị sang cùng đơn vị đo, rồi so sánh chúng với nhau. Cách giải: a) 5 ha 89m2 < 5,089ha b) 8ha 6dam2 > 8$\frac{5}{{100}}$ha c) 18, 064cm < 18m 64cm d) 750 kg > $\frac{3}{5}$ tấn Câu 11: Một thửa ruộng hình chữ nhật có chu vi 240 m và chiều dài gấp 3 lần chiều rộng. a) Tính diện tích của thửa ruộng. b) Người ta cấy lúa trên thửa ruộng, biết rằng cứ 100m2 thu được 50 kg thóc. Hỏi cả thửa ruộng đó thu hoạch được bao nhiêu tạ thóc? Phương pháp: Tìm nửa chu vi của thửa ruộng hình chữ nhật đó, rồi giải bài toán tìm hai số khi biết tổng và tỉ số của hai số đó để tìm chiều dài và chiều rộng, cuối cùng ta đi tính diện tích của thửa ruộng hình chữ nhật đó. Cách giải: Nửa chu vi thửa ruộng hình chữ nhật là: 240 : 2 = 120 (m) Ta có sơ đồ: Theo sơ đồ, tổng số phần bằng nhau là: 3 + 1 = 4 (phần) Chiều dài của thửa ruộng là: (120 : 4) x 3 = 90 (m) Chiều rộng của thửa ruộng là: 120 – 90 = 30 (m) Diện tích của thửa ruộng là: 90 x 30 = 2700 (m2) Đáp số: 2700 m2 b) Cả thửa ruộng đó thu hoạch được số thóc là: 50 x (2700 : 100) = 1350 (kg) Đổi 1350kg = 13,5 tạ. Đáp số: 13,5 tạ. Câu 12: Tính: $\frac{1}{{1 \times 2}} + \frac{1}{{2 \times 3}} + \frac{1}{{3 \times 4}} + \frac{1}{{4 \times 5}} + ... + \frac{1}{{99 \times 100}}$. Phương pháp: Nhận thấy $1 = 2 - 1 = 3 - 2 = 4 - 3 = ... = 100 - 99$ Từ đó ta biến đổi các tử số, thành các phép trừ tương ứng rồi biến đổi, tính toán để tìm ra kết quả. Cách giải: Ta có:
|















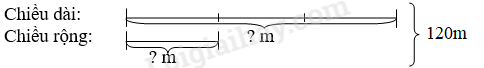







Danh sách bình luận