Lý thuyết Xác suất có điều kiện Toán 12 Chân trời sáng tạo1. Xác suất có điều kiện Quảng cáo
1. Xác suất có điều kiện
Ví dụ: Một hộp chứa ba tấm thẻ cùng loại ghi số lần lượt từ 1 đến 3. Bạn Hà lấy ra một cách ngẫu nhiên thẻ từ hộp, bỏ thẻ đó ra ngoài và lại lấy ra thêm một thẻ nữa. Xét các biến cố: A: "Thẻ lấy ra lần thứ nhất ghi số 1". B: "Thẻ lấy ra lần thứ hai ghi số 2". C: "Thẻ lấy ra lần thứ hai ghi số lẻ". a) Xác định không gian mẫu của phép thử. Viết tập hợp các kết quả thuận lợi cho mỗi biến cố có A, B, C. b) Tính xác suất để lấy ra lần thứ hai ghi số lẻ, biết rằng thế lấy ra lần thứ nhất ghi số 1. c) Tính xác suất để lấy ra lần thứ hai ghi số lẻ, biết rằng thế lấy ra lần thứ nhất ghi số 2. Giải: a) Không gian mẫu của phép thử: Ω = {(1; 2); (1; 3); (2; 1); (2; 3); (3; 1); (3; 2)}, trong đó (i; j) là kết quả lần thứ nhất lấy được thẻ ghi số i, lần thứ hai lấy được thẻ ghi số j. Tập hợp các kết quả thuận lợi cho biến cố A là {(1; 2); (1; 3)}. Tập hợp các kết quả thuận lợi cho biến cố B là {(2; 1); (2; 3)}. Tập hợp các kết quả thuận lợi cho biến cố C là {(2; 1); (3; 1); (1; 3); (2; 3)}. b) Xác suất cần tìm là P(C|A). Khi biến cố A xảy ra thì kết quả của phép thử là (1; 2) hoặc (1; 3). Trong hai kết quả đồng khả năng này chỉ có kết quả (1; 3) là thuận lợi cho biến cố C. Vậy xác suất để lấy ra lần thứ hai ghi số lẻ, biết rằng lần thứ nhất ghi số 1 là \(P(C|A) = \frac{1}{2}\). c) Xác suất cần tìm là P(C|B). Khi biến cố B xảy ra thì kết quả của phép thử là (2; 1) hoặc (2; 3). Cả hai kết quả này đều thuận lợi cho biến cố C. Vậy xác suất để lấy ra lần thứ hai ghi số lẻ, biết rằng lần thứ nhất ghi số 2 là P(C|B) = 1. 2. Công thức tính xác suất có điều kiện
Chú ý: - Ta cũng ký hiệu biến cố giao của hai biến cố A và B là AB. - Trong thực tế, người ta thường dùng tỷ lệ phần trăm để mô tả xác suất. Ví dụ: Một công ty bảo hiểm nhận thấy 48% số người mua bảo hiểm ô tô là phụ nữ và có 36% số người mua bảo hiểm ô tô là phụ nữ trên 45 tuổi. a) Biết một người mua bảo hiểm ô tô là phụ nữ, tính xác suất người đó trên 45 tuổi. b) Tính tỉ lệ người trên 45 tuổi trong số những người phụ nữ mua bảo hiểm ô tô. Giải: a) Gọi A là biến cố “Người mua bảo hiểm ô tô là phụ nữ”, B là biến cố “Người mua bảo hiểm ô tô trên 45 tuổi”. Ta cần tính P(B|A). Do có 48% người mua bảo hiểm ô tô là phụ nữ nên P(A) = 0,48. Do có 36% số người mua bảo hiểm ô tô là phụ nữ trên 45 tuổi nên P(AB) = 0,36. Vậy \(P\left( {B|A} \right) = \frac{{P(AB)}}{{P(A)}} = \frac{{0,36}}{{0,48}} = 0,75.\) b) Trong số những phụ nữ mua bảo hiểm ô tô thì có 75% người trên 45 tuổi. Chú ý: - Từ công thức xác suất có điều kiện, với P(B) > 0, ta có P(AB) = P(B).P(A|B). - Trong trường hợp tổng quát, người ta chứng minh được rằng với A, B là hai biến cố có bất kì thì:
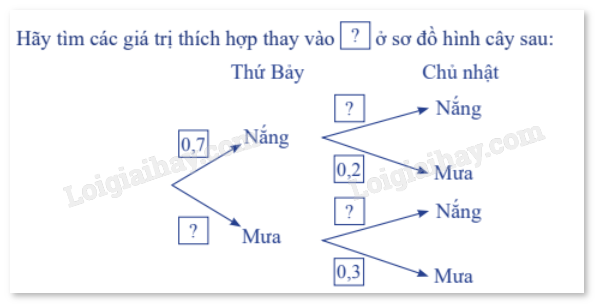
3. Sơ đồ hình cây Ví dụ: Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7. Giải:
Gọi A là biến cố "Ngày thứ Bảy trời nắng" và B là biến cố "Ngày Chủ nhật trời mưa". Ta có P(A) = 0,7; P(B|A) = 0,2; P(B|A̅) = 0,3. Do đó P(A̅) = 1 - P(A) = 0,3; P(B|A) = 0,8; P(B|A̅) = 1 - P(B|A) = 0,7. Áp dụng công thức nhân xác suất, ta có xác suất trời nắng vào thứ Bảy và trời mưa vào Chủ nhật là P(AB) = P(A)P(B|A) = 0,7.0,2 = 0,14. Tương tự, ta có: P(A̅B) = P(A̅).P(B|A̅) = 0,3.0,8 = 0,56; P(AB̅) = P(A).P(B̅|A) = 0,7.0,3 = 0,09; P(A̅B̅) = P(A̅)P(B̅|A̅) = 0,3.0,7 = 0,21. Ta có thể biểu diễn các kết quả trên theo đồ thị hình cây như sau:
Nhận xét: - Xác suất của các nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện. - Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.
|






















Danh sách bình luận