Trang chủ
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức

Lý thuyết Nguyên hàm Toán 12 Kết nối tri thức

Lý thuyết Nguyên hàm

Quảng cáo

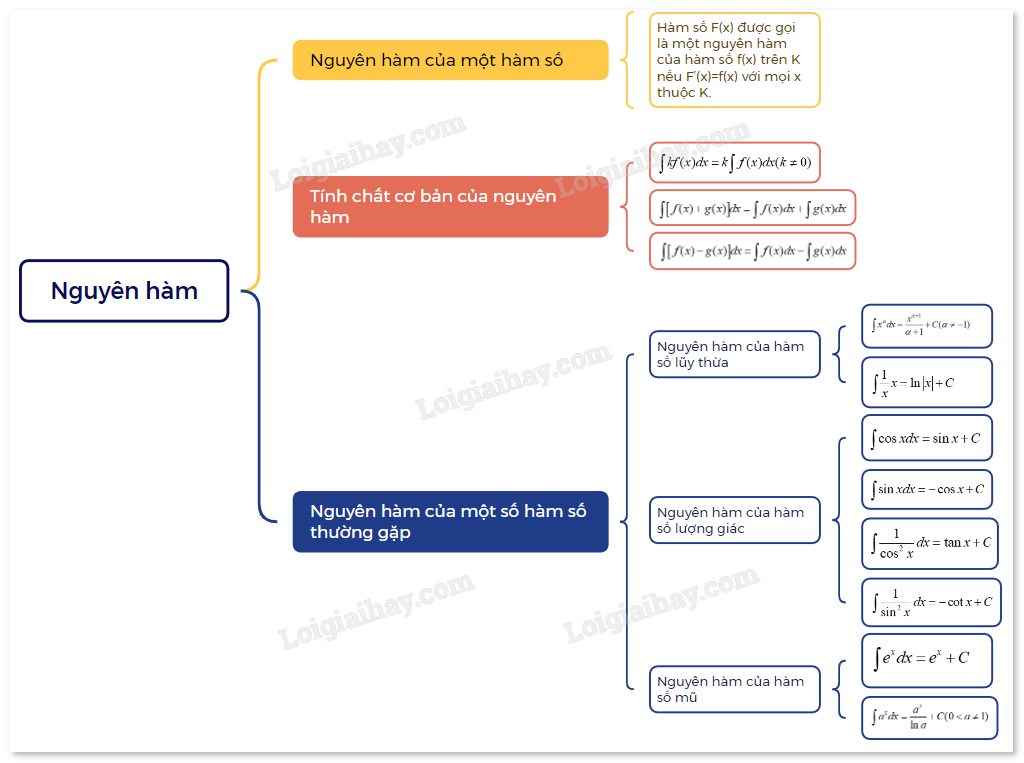
1. Nguyên hàm của một hàm số

Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K.

Chú ý:

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K

Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + C là họ các nguyên hàm của f(x) trên K, kí hiệu bởi \(\int {f(x)dx} \).

2. Tính chất cơ bản của nguyên hàm

  • \(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \)
  • \(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \)
  • \(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \)

3. Nguyên hàm của một số hàm số thường gặp

a) Nguyên hàm của hàm số lũy thừa

Hàm số lũy thừa \(y = {x^\alpha }(\alpha  \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha  - 1}}\)

  • \(\int {{x^\alpha }dx = \frac{{{x^{\alpha  + 1}}}}{{\alpha  + 1}} + C(\alpha  \ne  - 1)} \)
  • \(\int {\frac{1}{x}x = \ln \left| x \right| + C} \)

b) Nguyên hàm của hàm số lượng giác

  • \(\int {\cos xdx = \sin x + C} \)
  • \(\int {\sin xdx =  - \cos x + C} \)
  • \(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \)
  • \(\int {\frac{1}{{{{\sin }^2}x}}dx =  - \cot x + C} \)

c) Nguyên hàm của hàm số mũ

  • \(\int {{e^x}dx = {e^x} + C} \)
  • \(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \)

 

 

Quảng cáo
Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
close