Giải mục 3 trang 8, 9, 10 SGK Toán 12 tập 2 - Kết nối tri thứcNguyên hàm của một số hàm số thường gặp Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
? Trả lời câu hỏi ? trang 8 SGK Toán 12 Kết nối tri thức Bằng cách viết lại các hàm số sau dưới dạng lũy thừa \(y = {x^\alpha }\left( {x > 0} \right)\), hãy tính đạo hàm của các hàm số sau với \(x > 0\): \(y = \frac{1}{{{x^4}}},y = {x^{\sqrt 2 }},y = \frac{1}{{\sqrt[3]{x}}}\). Phương pháp giải: Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\). Lời giải chi tiết: Ta có: \(y = \frac{1}{{{x^4}}} = {x^{ - 4}}\) nên \(y' = - 4{x^{ - 5}}\); \(y = {x^{\sqrt 2 }} = {x^{\frac{1}{2}}}\) nên \(y' = \frac{1}{2}{x^{ - \frac{1}{2}}} = \frac{1}{{2\sqrt x }}\), \(y = \frac{1}{{\sqrt[3]{x}}} = {x^{\frac{{ - 1}}{3}}}\) nên \(y' = \frac{{ - 1}}{3}{x^{\frac{{ - 4}}{3}}} = \frac{{ - 1}}{{3{x^{\frac{4}{3}}}}}\). HĐ5 Trả lời câu hỏi Hoạt động 5 trang 8 SGK Toán 12 Kết nối tri thức a) Với \(\alpha \ne - 1\), tính đạo hàm của hàm số \(y = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left( {x > 0} \right)\). b) Cho hàm số \(y = \ln \left| x \right|\left( {x \ne 0} \right)\). Tính đạo hàm của hàm số này trong hai trường hợp: \(x > 0\) và \(x < 0\). Phương pháp giải: Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K. Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số. Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\). Lời giải chi tiết: a) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\). b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\). Với \(x > 0\) thì \(y' = \frac{1}{x}\). Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\). LT5 Trả lời câu hỏi Luyện tập 5 trang 9 SGK Toán 12 Kết nối tri thức Tìm: a) \(\int {\frac{1}{{{x^4}}}dx} \); b) \(\int {x\sqrt x dx\left( {x > 0} \right)} \); c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx\left( {x > 0} \right)} \). Phương pháp giải: Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \) Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \) Sử dụng kiến thức về nguyên hàm của hàm số lũy thừa để tính: \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\left( {\alpha \ne - 1} \right)\) Lời giải chi tiết: a) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\); b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\); c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \) \( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\). HĐ6 Trả lời câu hỏi Hoạt động 6 trang 9 SGK Toán 12 Kết nối tri thức a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
Phương pháp giải: a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính: \(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\) b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K. Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số. Lời giải chi tiết: a)
b)
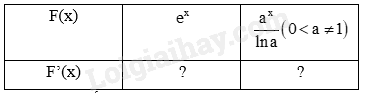
LT6 Trả lời câu hỏi Luyện tập 6 trang 9 SGK Toán 12 Kết nối tri thức Tìm: a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \); b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \). Phương pháp giải: Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \) Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \) Sử dụng kiến thức về nguyên hàm của hàm số lượng giác để tính: \(\int {\cos x} dx = \sin x + C,\int {\sin x} dx = - \cos x + C,\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C,\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\) Lời giải chi tiết: a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\); b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\). HĐ7 Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 12 Kết nối tri thức a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
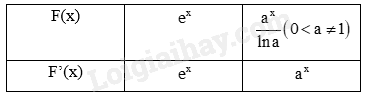
Phương pháp giải: a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)' = {e^x},\left( {{a^x}} \right)' = {a^x}.\ln a\) b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K. Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số. Lời giải chi tiết: a)
b)
LT7 Trả lời câu hỏi Luyện tập 7 trang 10 SGK Toán 12 Kết nối tri thức Tìm: a) \(\int {{4^x}dx} \); b) \(\int {\frac{1}{{{e^x}}}dx} \); c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \). Phương pháp giải: Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \) Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \) Sử dụng kiến thức về nguyên hàm của hàm số mũ để tính: \(\int {{e^x}dx} = {e^x} + C,\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\left( {0 < a \ne 1} \right)\). Lời giải chi tiết: a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\); b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\); c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx \) \(= \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
|

















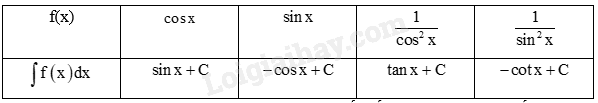








Danh sách bình luận