Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo

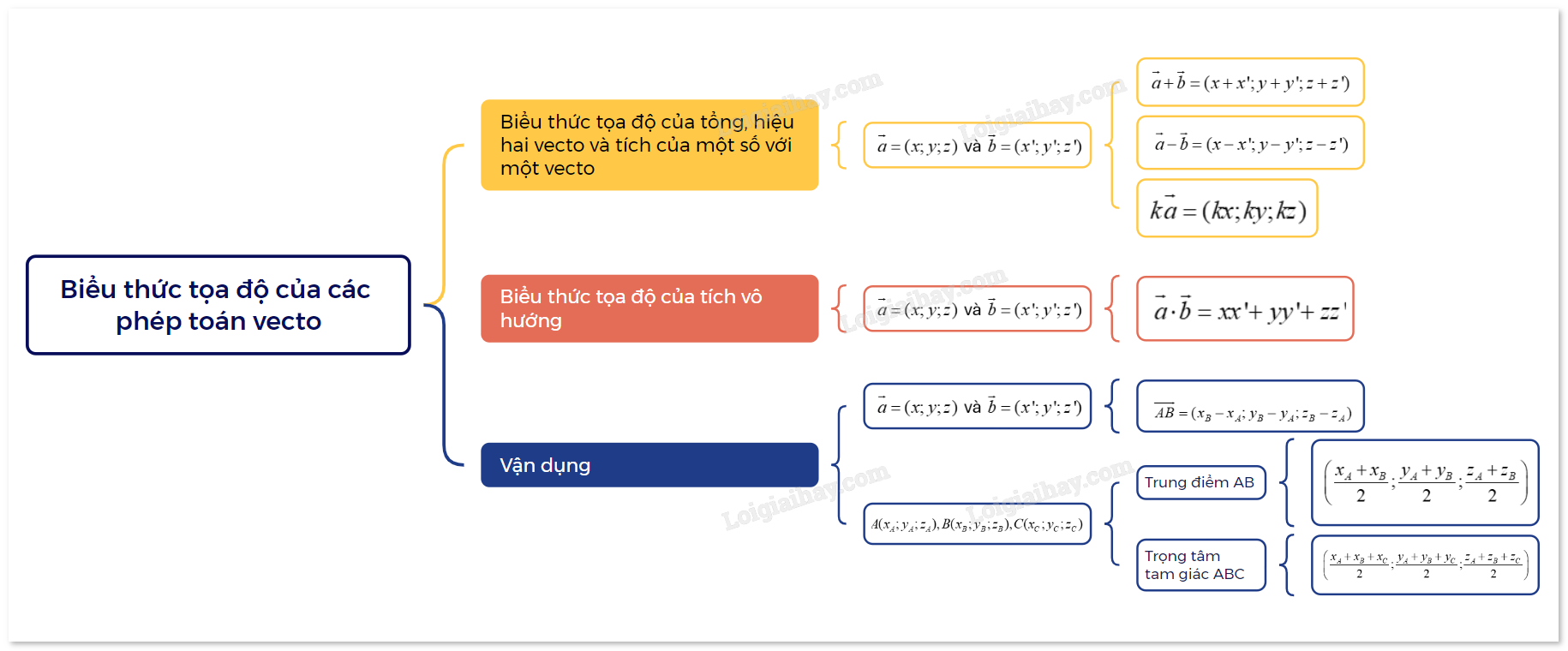
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a  = (x;y;z)\) và \(\overrightarrow b  = (x';y';z')\). Ta có:

• \(\overrightarrow a  + \overrightarrow b  = (x + x';y + y';z + z')\).
• \(\overrightarrow a  - \overrightarrow b  = (x - x';y - y';z - z')\).
• \(k\overrightarrow a  = (kx;ky;kz)\) với k là một số thực.

Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a  = (x;y;z)\) và \(\overrightarrow b  = (x';y';z')\) được xác định bởi công thức:

\(\overrightarrow a  \cdot \overrightarrow b  = xx' + yy' + zz'\).

Trong không gian Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Ta có:

Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A})\), \(B({x_B};{y_B};{z_B})\), \(C({x_C};{y_C};{z_C})\). Khi đó:

• Tọa độ trung điểm của đoạn thẳng AB là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\).
• Tọa độ trọng tâm tam giác ABC là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\).