Giải mục II trang 109, 110 SGK Toán 7 tập 2 - Cánh diềuII. Tính chất ba đường phân giác của tam giác Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
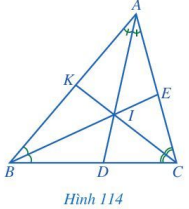
II. Tính chất ba đường phân giác của tam giác HĐ 2 Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.
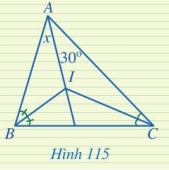
Phương pháp giải: Quan sát Hình 114 để xem các đường phân giác AD, BE, CK có cùng đi qua một điểm hay không. Lời giải chi tiết: Các đường phân giác AD, BE, CK có cùng đi qua một điểm là điểm I. LT - VD 2 Tìm số đo x trong Hình 115.
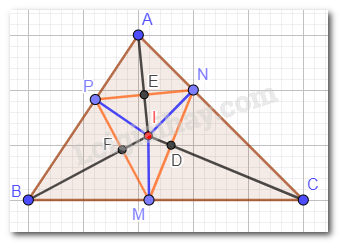
Phương pháp giải: Dựa vào tính chất của ba đường phân giác trong tam giác. Lời giải chi tiết: I là giao điểm của hai đường phân giác góc B và góc C. Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C. Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \). LT - VD 3 Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN. Phương pháp giải: Dựa vào tính chất của ba đường phân giác trong tam giác và tính chất của đường trung tuyến (đi qua trung điểm và vuông góc tại trung điểm). Lời giải chi tiết:
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM. Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP. Xét tam giác vuông INC và tam giác vuông IMC: IC chung; IN = IM. Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng). Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng). \(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng). Xét hai tam giác IDN và IDM có: ID chung; \(\widehat {NID} = \widehat {MID}\); IN = IM. Vậy \(\Delta IDN = \Delta IDM\)(c.g.c) \(\Rightarrow DN = DM\) ( 2 cạnh tương ứng); \(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng) Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù) \(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\). Suy ra: IC là đường trung trực của cạnh MN. Tương tự ta có: IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
|




















Danh sách bình luận